Teorema egregio
Il Teorema Egregio di Gauss (latino per "Teorema notevole") è un importante risultato della geometria differenziale dimostrato da Carl Friedrich Gauss. Il teorema riguarda la curvatura delle superfici. Il teorema afferma che la curvatura può essere determinata misurando solo gli angoli, le distanze e i loro tassi su una superficie. Non c'è bisogno di parlare del modo particolare in cui la superficie è inserita nello spazio euclideo tridimensionale circostante. In altre parole, la curvatura gaussiana di una superficie non cambia se si piega la superficie senza allungarla.
Gauss presentò il teorema in questo modo (tradotto dal latino):
Per questa ragione la formula dell'articolo precedente porta al notevole Teorema. Se una superficie curva si sviluppa su qualsiasi altra superficie, la misura della curvatura in ogni punto rimane invariata.
Il teorema è "notevole" perché la definizione di partenza della curvatura gaussiana fa uso diretto della posizione della superficie nello spazio. Quindi è abbastanza sorprendente che il risultato non dipenda dalla sua incorporazione nonostante tutte le deformazioni di flessione e torsione subite.
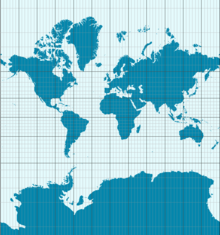
Una conseguenza del Theorema Egregium è che la Terra non può essere visualizzata su una mappa senza distorsioni. La proiezione di Mercatore, mostrata qui, conserva gli angoli ma cambia l'area. Per esempio, l'Antartide è mostrata molto più grande di quanto sia in realtà.
Domande e risposte
D: Che cos'è il Teorema Egregium di Gauss?
R: Il Teorema Egregium di Gauss è un importante risultato della geometria differenziale che riguarda la curvatura delle superfici, dimostrato da Carl Friedrich Gauss.
D: Come si può determinare la curvatura, secondo il Teorema Egregium di Gauss?
R: Secondo il Teorema Egregium di Gauss, la curvatura può essere determinata solo misurando gli angoli, le distanze e i loro tassi su una superficie.
D: È necessario parlare del modo particolare in cui la superficie è inserita nello spazio euclideo tridimensionale circostante per determinare la curvatura?
R: No, non è necessario parlare del modo particolare in cui la superficie è inserita nello spazio euclideo tridimensionale circostante per determinare la curvatura secondo il Teorema Egregium di Gauss.
D: La curvatura gaussiana di una superficie cambia se si piega la superficie senza allungarla?
R: No, la curvatura gaussiana di una superficie non cambia se si piega la superficie senza allungarla, secondo il Teorema Egregium di Gauss.
D: Chi ha presentato il teorema in questo modo?
R: Gauss ha presentato il teorema in questo modo.
D: Per cosa è notevole il teorema?
R: Il teorema è 'notevole' perché la definizione iniziale della curvatura gaussiana fa uso diretto della posizione della superficie nello spazio. Quindi è sorprendente che il risultato non dipenda dal suo incorporamento, nonostante tutte le deformazioni di flessione e torsione subite.
D: In che modo Gauss ha presentato il teorema?
R: Gauss presentò il teorema in modo tale che se una superficie curva viene sviluppata su qualsiasi altra superficie, la misura della curvatura in ogni punto rimane invariata.
Cerca nell'enciclopedia