Teoria delle travi di Eulero-Bernoulli
La teoria delle travi di Eulero-Bernoulli (conosciuta anche come teoria delle travi dell'ingegnere o teoria classica delle travi) è un metodo semplice per calcolare la flessione delle travi quando viene applicato un carico. Si applica a piccole deflessioni (quanto qualcosa si muove) di una trave senza considerare gli effetti delle deformazioni di taglio. Pertanto, può essere considerato un caso speciale della teoria delle travi di Timoshenko. Fu introdotta per la prima volta intorno al 1750. Ha guadagnato popolarità durante lo sviluppo della Torre Eiffel e della ruota panoramica alla fine del XIX secolo. Dopo di che, è stata usata in molti campi dell'ingegneria, tra cui l'ingegneria meccanica e l'ingegneria civile. Anche se sono stati sviluppati altri metodi avanzati, la teoria delle travi di Eulero-Bernoulli è ancora ampiamente utilizzata per la sua semplicità.
Una trave di vetro vibrante che mostra la flessione delle travi che può essere stimata usando la teoria delle travi di Eulero-Bernoulli.
Storia
Leonhard Euler e Daniel Bernoulli furono i primi a mettere insieme la teoria nel 1750. A quel tempo, la scienza e l'ingegneria erano viste diversamente da oggi. Le teorie matematiche come la teoria delle travi di Eulero-Bernoulli non erano affidabili per l'uso ingegneristico pratico. Ponti ed edifici continuarono ad essere progettati con gli stessi metodi fino alla fine del XIX secolo. Questo è quando la Torre Eiffel e la ruota di Ferris mostrarono la validità della teoria su una scala più grande.
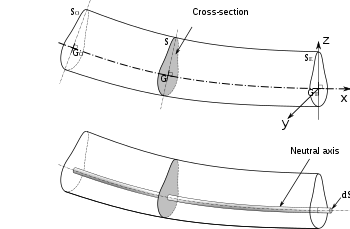
Disegno di una sezione trasversale di una trave piegata che mostra l'asse neutro
Equazione della trave statica
L'equazione di Eulero-Bernoulli descrive la relazione tra la deflessione della trave e il carico applicato come mostrato di seguito:
d 2 d x 2 ( E I d 2 w d x 2 ) = q {displaystyle {frac {mathrm {d} ^{2}}{mathrm {d} x^{2}}} a sinistra (EI{frac {mathrm {d} ^{2}w}{mathrm {d} x^{2}} a destra)=q\,} 
Dove w ( x ) {displaystyle w(x)} 
descrive la deflessione della trave nella 
direzione z {displaystyle z} in qualche posizione x {displaystyle x}
. q {displaystyle q}
è un carico distribuito, in altre parole una forza per unità di lunghezza (analogo alla pressione che è una forza per area); può essere una funzione di x {displaystyle x} , w {displaystyle w} 
o di altre variabili.
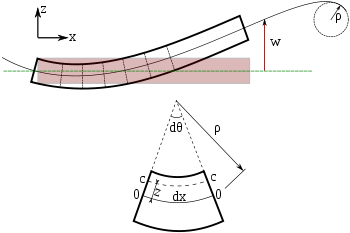
Flessione di una trave di Eulero-Bernoulli. Ogni sezione trasversale della trave è a 90 gradi rispetto all'asse neutro.
Domande e risposte
D: Che cos'è la teoria delle travi di Eulero-Bernoulli?
R: La teoria delle travi di Eulero-Bernoulli è un metodo semplice utilizzato per calcolare la flessione delle travi quando viene applicato un carico, senza considerare gli effetti delle deformazioni di taglio.
D: Quando è stata introdotta la teoria delle travi di Eulero-Bernoulli?
R: La teoria delle travi di Eulero-Bernoulli è stata introdotta per la prima volta intorno al 1750.
D: La teoria delle travi di Eulero-Bernoulli è stata utilizzata nello sviluppo della Torre Eiffel e della ruota panoramica?
R: Sì, la teoria delle travi di Eulero-Bernoulli ha guadagnato popolarità durante lo sviluppo della Torre Eiffel e della ruota panoramica alla fine del XIX secolo.
D: Quali sono alcuni campi dell'ingegneria in cui è stata utilizzata la teoria delle travi di Eulero-Bernoulli?
R: La teoria delle travi di Eulero-Bernoulli è stata utilizzata in molti campi dell'ingegneria, tra cui l'ingegneria meccanica e l'ingegneria civile.
D: La teoria delle travi di Eulero-Bernoulli è ancora molto utilizzata oggi?
R: Sì, la teoria delle travi di Eulero-Bernoulli è ancora oggi molto utilizzata per la sua semplicità, anche se sono stati sviluppati altri metodi avanzati.
D: A quali tipi di deflessioni di una trave si applica la teoria delle travi di Eulero-Bernoulli?
R: La teoria delle travi di Eulero-Bernoulli si applica a piccole deflessioni di una trave.
D: La teoria delle travi di Eulero-Bernoulli tiene conto degli effetti delle deformazioni di taglio?
R: No, la teoria delle travi di Eulero-Bernoulli non considera gli effetti delle deformazioni di taglio.
