Teorema degli schemi di Holland: definizione e ruolo negli algoritmi genetici

Teorema degli schemi di Holland: definizione, implicazioni e ruolo negli algoritmi genetici. Spiegazione chiara su schemi, fitness e dinamiche evolutive.

Autore: Leandro Alegsa

25-02-2026 14:41

Il teorema dello schema di Holland, chiamato anche il teorema fondamentale degli algoritmi genetici, è una disuguaglianza ottenuta tramite un'operazione di coarse-graining applicata a un'equazione per la dinamica evolutiva della popolazione. Enunciato informalmente, il teorema afferma che schemi brevi e di basso ordine con fitness superiore alla media tendono ad aumentare in frequenza nelle generazioni successive. Proposto da John Holland negli anni '70, è stato a lungo considerato una giustificazione teorica della potenza degli algoritmi genetici. Tuttavia, la portata interpretativa del teorema è stata oggetto di critiche in numerosi lavori di letteratura scientifica: il risultato è una disuguaglianza (un limite inferiore sull'aspettativa) e può essere visto come un caso particolare dell'equazione di Price quando si usa la funzione indicatrice dello schema come misura macroscopica.

Che cos'è uno schema

Uno schema è un modello che identifica un sottoinsieme di stringhe (tipicamente binarie) che condividono valori fissati in certe posizioni e sono indifferentemente qualsiasi valore nelle altre posizioni. Ad esempio, per stringhe di lunghezza l=6 lo schema 1*01** identifica tutte le stringhe che hanno '1' nella prima posizione, qualsiasi simbolo nella seconda, '0' nella terza, '1' nella quarta e qualsiasi simbolo nelle ultime due posizioni.

Formalmente, gli schemi sono un caso speciale di insiemi di cilindri e quindi costituiscono uno spazio topologico particolare all'interno dello spazio delle stringhe.

Notazione e termini principali

m(H, t): numero (o frequenza) di individui nella popolazione alla generazione t che corrispondono allo schema H.
f(H): fitness media degli individui che appartengono a H.
f̄: fitness media dell'intera popolazione.
l: lunghezza delle stringhe (numero di loci).
o(H) (ordine dello schema): numero di posizioni specificate (non wildcard) in H.
δ(H) (lunghezza definente): distanza tra la prima e l'ultima posizione specificata di H (indice_last − indice_first).
p_c: probabilità di crossover (es. single-point crossover).
p_m: probabilità di mutazione per singolo bit (o locus).

Enunciato formale (versione comunemente riportata)

Per una popolazione sottoposta a selezione proporzionale alla fitness, crossover a singolo punto con probabilità p_c e mutazione con probabilità p_m per bit, l'aspettativa del numero di copie dello schema H nella generazione successiva soddisfa la disuguaglianza:

E[m(H, t+1)] ≥ m(H, t) * (f(H) / f̄) * [1 - p_c * (δ(H) / (l - 1))] * (1 - p_m)^{o(H)}

Questa formula fornisce un limite inferiore sull'aspettativa: la prima parte, m(H,t) * (f(H)/f̄), è l'effetto della selezione (schemi con fitness superiore alla media vengono amplificati), mentre i fattori tra parentesi rappresentano la probabilità che lo schema sopravviva agli operatori genetici (crossover e mutazione).

Interpretazione intuitiva

Schemi con fitness media f(H) > f̄ sono favoriti dalla selezione.
Schemi brevi (piccola δ(H)) sono meno vulnerabili alla rottura provocata dal crossover.
Schemi di basso ordine (piccolo o(H)) hanno maggiore probabilità di non essere alterati dalla mutazione (fattore (1 - p_m)^{o(H)}).
Da qui nasce l'idea dei "building blocks": combinazioni brevi, semplici e sopra la media si propagano e possono combinarsi tra loro per creare soluzioni migliori.

Esempio pratico

Consideriamo stringhe di lunghezza l = 6 e lo schema H = 1*01**. Le posizioni fissate sono 1, 3 e 4, quindi o(H) = 3. La prima posizione fissata è 1 e l'ultima è 4, dunque δ(H) = 4 − 1 = 3. Se p_c = 0.7 e p_m = 0.01, il fattore di sopravvivenza approssimativo dovuto agli operatori è [1 − 0.7*(3/5)]*(1 − 0.01)^{3}, che mostra come ordine e lunghezza definente influenzino la probabilità che uno schema venga preservato.

Limitazioni e critiche

Pur essendo storicamente influente, il teorema degli schemi ha limiti importanti:

È una disuguaglianza che dà solo un limite inferiore sull'aspettativa, non una previsione esatta del comportamento reale della popolazione.
Non prende in considerazione la creazione di nuovi schemi tramite crossover (il teorema si concentra principalmente sulla sopravvivenza degli schemi esistenti), quindi trascura parte della dinamica creativa degli AG.
In problemi con forte epistasis (interazioni tra geni) o in funzioni decorative, schemi brevi e di basso ordine potrebbero non essere rappresentativi dei componenti utili della soluzione; la semplice proliferazione di schemi sopra la media non garantisce la convergenza verso soluzioni globalmente buone.
Interpretazioni semplicistiche del teorema (come “gli algoritmi genetici funzionano grazie solo ai piccoli schemi”) sono fuorvianti: la performance pratica dipende anche da rappresentazione, design degli operatori, dimensione della popolazione e apprendimento del linkage.

Relazione con l'equazione di Price e sviluppi teorici

Il teorema dello schema può essere ricondotto all'equazione di Price se si considera la funzione indicatrice dello schema come osservabile macroscopica: sotto questo punto di vista il risultato di Holland è un caso particolare di un'analisi più generale del cambiamento di medie dovuto a selezione e trasmissione. Negli anni successivi sono state proposte generalizzazioni più precise e approcci alternativi (modelli di Markov, analisi tramite l'equazione di Price, modelli basati su distribuzioni come gli estimation of distribution algorithms) che cercano di descrivere in modo più completo la dinamica degli algoritmi evolutivi.

Ruolo negli algoritmi genetici moderni

Il teorema degli schemi ha avuto il merito di introdurre concetti utili (ordine, lunghezza definente, importanza degli schemi con fitness sopra la media) e di formulare la celebre ipotesi dei "building blocks". Nella pratica odierna, tuttavia, la progettazione di algoritmi genetici efficaci spesso incorpora tecniche che vanno oltre la semplice considerazione degli schemi: apprendimento del linkage, crossover ricombinante attento alle dipendenze, operatori adattativi e approcci basati su modelli probabilistici. Queste estensioni affrontano alcune delle debolezze che emergono dall'interpretazione letterale del teorema.

Conclusione

Il teorema dello schema di Holland rimane un risultato storico e concettualmente importante nella teoria degli algoritmi genetici: spiega come, in presenza di selezione e a parità di condizioni, schemi corti e a basso ordine con fitness superiore alla media tendano ad aumentare nella popolazione. Tuttavia, la sua portata è limitata — si tratta di un limite inferiore e non di una descrizione completa della dinamica degli AG — e la sua interpretazione pratica deve essere integrata con analisi più approfondite e con tecniche progettuali moderne.

Nota: uno schema definisce sempre un sottoinsieme di stringhe; gli schemi possono essere studiati anche nella cornice più generale degli insiemi di cilindri e della topologia discreta su spazi di stringhe, come evidenziato anche nella letteratura relativa agli sottoinsiemi e agli spazi topologici.

Descrizione

Consideriamo stringhe binarie di lunghezza 6. Lo schema 1*10*1 descrive l'insieme di tutte le stringhe di lunghezza 6 con 1 nelle posizioni 1, 3 e 6 e uno 0 nella posizione 4. L'* è un simbolo jolly, il che significa che le posizioni 2 e 5 possono avere sia il valore di 1 che di 0. Lo schema o ( H ) è definito come uno schema che ha il valore di 1. L'* è un simbolo jolly, il che significa che le posizioni 2 e 5 possono avere un valore di 1 o 0. L'ordine di uno schema o ( H ) {displaystyle o(H)} $o(H)$ è definito come il numero di posizioni fisse nello schema, mentre la lunghezza di definizione δ ( H ) {displaystyle \delta (H)} $\delta (H)$ è la distanza tra la prima e l'ultima posizione specifica. L'ordine di 1*10*1 è 4 e la sua lunghezza determinante è 5. Il fitness di uno schema è il fitness medio di tutte le stringhe che corrispondono allo schema. Il fitness di una stringa è una misura del valore della soluzione del problema codificata, come calcolato da una funzione di valutazione specifica del problema. Usando i metodi consolidati e gli operatori genetici degli algoritmi genetici, il teorema dello schema afferma che gli schemi brevi e di basso ordine con fitness superiore alla media aumentano esponenzialmente nelle generazioni successive. Espresso come un'equazione:

E ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . E ( m(H,t+1) ) ≥ m ( H,t ) f ( H ) a t [ 1 - p ] . (m(H,t+1))\geq {m(H,t)f(H) su a_{t}}[1-p]. } $\operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p].$

Qui m ( H , t ) {displaystyle m(H,t)} $m(H,t)$ è il numero di stringhe appartenenti allo schema H {displaystyle H} $H$ alla generazione t {displaystyle t} $t$ , f ( H ) {displaystyle f(H)} $f(H)$ è la fitness media osservata dello schema H {displaystyle H} $H$ e a t {displaystyle a_{t}} $a_{t}$ è la fitness media osservata alla generazione t {displaystyle t} $t$ . La probabilità di interruzione p {displaystyle p} $p$ è la probabilità che il crossover o la mutazione distruggano lo schema H {displaystyle H} $H$ . Può essere espressa come:

p = δ ( H ) l - 1 p c + o ( H ) p m {displaystyle p={delta (H) \over l-1}p_{c}+o(H)p_{m}} $p={\delta (H) \over l-1}p_{c}+o(H)p_{m}$

dove o ( H ) {displaystyle o(H)} $o(H)$ è l'ordine dello schema, l {displaystyle l} $l$ è la lunghezza del codice, p m {displaystyle p_{m}} $p_{m}$ è la probabilità di mutazione e p c {displaystyle p_{c}} $p_{c}$ è la probabilità di crossover. Quindi uno schema con una lunghezza di definizione più breve δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ ha meno probabilità di essere interrotto.
Un punto spesso frainteso è perché il teorema dello schema è una disuguaglianza piuttosto che un'uguaglianza. La risposta è infatti semplice: il Teorema trascura la piccola, ma non nulla, probabilità che una stringa appartenente allo schema H {displaystyle H} $H$ venga creata "da zero" per mutazione di una singola stringa (o ricombinazione di due stringhe) che non apparteneva a H {displaystyle H} $H$ nella generazione precedente.

Limitazione

Il teorema dello schema vale nell'ipotesi di un algoritmo genetico che mantiene una popolazione infinitamente grande, ma non sempre si applica alla pratica (finita): a causa di un errore di campionamento nella popolazione iniziale, gli algoritmi genetici possono convergere su schemi che non hanno alcun vantaggio selettivo. Questo accade in particolare nell'ottimizzazione multimodale, dove una funzione può avere più picchi: la popolazione può andare alla deriva per preferire uno dei picchi, ignorando gli altri.

La ragione per cui il teorema dello schema non può spiegare la potenza degli algoritmi genetici è che vale per tutte le istanze del problema e non può distinguere tra i problemi in cui gli algoritmi genetici funzionano male e i problemi in cui gli algoritmi genetici funzionano bene.

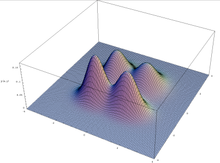
Tracciato di una funzione multimodale in due variabili.

Domande e risposte

D: Cos'è il teorema dello schema di Holland?

R: Il teorema dello schema di Holland è un teorema relativo agli algoritmi genetici che afferma che gli individui con una fitness superiore alla media hanno maggiori probabilità di prevalere.

D: Chi ha proposto il teorema dello schema di Holland e quando?

R: John Holland ha proposto il teorema dello schema di Holland negli anni '70.

D: Che cos'è uno schema nel contesto degli algoritmi genetici?

R: Nel contesto degli algoritmi genetici, uno schema è un modello che identifica un sottoinsieme di stringhe con somiglianze in determinate posizioni di stringhe.

D: Qual è l'interpretazione del teorema dello schema di Holland, utilizzato come base per le spiegazioni della potenza degli algoritmi genetici?

R: L'interpretazione del teorema dello schema di Holland, utilizzato come base per le spiegazioni della potenza degli algoritmi genetici, è che gli individui con una fitness superiore alla media hanno maggiori probabilità di prevalere.

D: Cosa hanno dimostrato le critiche al teorema dello schema di Holland?

R: Le critiche al teorema dello schema di Holland hanno dimostrato che si tratta di un caso speciale dell'equazione di Price con la funzione indicatore dello schema come misura macroscopica.

D: Qual è un caso speciale di insiemi di cilindri?

R: Gli schemi sono un caso speciale di insiemi cilindrici.

D: Che tipo di spazio formano gli schemi?

R: Gli schemi formano uno spazio topologico.

Cerca nell'enciclopedia