Regressione lineare
La regressione lineare è un modo per spiegare la relazione tra una variabile dipendente e una o più variabili esplicative utilizzando una linea retta. È un caso particolare di analisi della regressione.
La regressione lineare è stato il primo tipo di analisi di regressione da studiare rigorosamente. Ciò è dovuto al fatto che i modelli che dipendono linearmente dai loro parametri sconosciuti sono più facili da adattare rispetto ai modelli che non sono in relazione lineare con i loro parametri. Inoltre, le proprietà statistiche degli stimatori risultanti sono più facili da determinare.
La regressione lineare ha molti usi pratici. La maggior parte delle applicazioni rientra in una delle seguenti due grandi categorie:
- La regressione lineare può essere usata per adattare un modello predittivo ad un insieme di valori osservati (dati). Questo è utile, se l'obiettivo è la previsione, o la previsione, o la riduzione. Dopo aver sviluppato un tale modello, se viene dato un valore addizionale di X senza il suo valore di y, il modello adattato può essere usato per fare una previsione del valore di y.
- Data una variabile y e un certo numero di variabili X1, ..., Xp che possono essere correlate a y, l'analisi di regressione lineare può essere applicata per quantificare la forza della relazione tra y e l'Xj, per valutare quale Xj non ha alcuna relazione con y, e per identificare quali sottoinsiemi dell'Xj contengono informazioni ridondanti su y.
I modelli di regressione lineare cercano di ridurre al minimo la distanza verticale tra la linea e i punti dati (ad es. i residui). Questo si chiama "adattare la linea ai dati". Spesso, i modelli di regressione lineare cercano di minimizzare la somma dei quadrati dei residui (minimi quadrati), ma esistono altri modi di adattamento. Essi includono la minimizzazione della "mancanza di adattamento" in qualche altra norma (come con la regressione delle deviazioni meno assolute), o la minimizzazione di una versione penalizzata della funzione di perdita dei minimi quadrati come nella regressione di cresta. L'approccio dei minimi quadrati può anche essere usato per adattare modelli che non sono lineari. Come indicato sopra, i termini "minimi quadrati" e "modello lineare" sono strettamente collegati, ma non sono sinonimi.
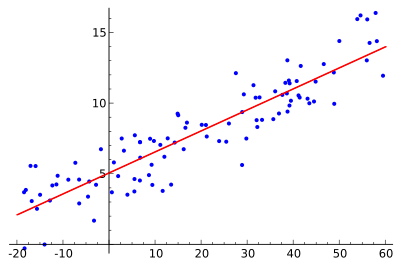
L'idea è quella di trovare la curva rossa, i punti blu sono campioni reali. Con la regressione lineare tutti i punti possono essere collegati usando una singola linea retta. Questo esempio utilizza una semplice regressione lineare, dove il quadrato della distanza tra la linea rossa ed ogni punto campione è ridotto al minimo.
Utilizzo
Economia
La regressione lineare è il principale strumento analitico in economia. Ad esempio, viene utilizzata per indovinare la spesa per i consumi, la spesa per gli investimenti fissi, gli investimenti in inventario, gli acquisti delle esportazioni di un paese, la spesa per le importazioni, la domanda di contenere la liquidità, la domanda di lavoro e l'offerta di lavoro.
Domande e risposte
D: Cos'è la regressione lineare?
R: La regressione lineare è un modo per vedere come cambia qualcosa quando cambiano altre cose, utilizzando la matematica. Utilizza una variabile dipendente e una o più variabili esplicative per creare una linea retta, nota come "linea di regressione".
D: Quali sono i vantaggi della regressione lineare?
R: I modelli che dipendono linearmente dai loro parametri sconosciuti sono più facili da adattare rispetto ai modelli che sono correlati in modo non lineare ai loro parametri. Inoltre, le proprietà statistiche degli stimatori risultanti sono più facili da determinare.
D: Quali sono gli usi pratici della regressione lineare?
R: La regressione lineare può essere utilizzata per adattare un modello predittivo ai valori osservati (dati), al fine di fare previsioni, pronostici o riduzioni. Può anche essere utilizzata per quantificare la forza delle relazioni tra le variabili e identificare sottoinsiemi di dati che contengono informazioni ridondanti su un'altra variabile.
D: In che modo i modelli di regressione lineare cercano di minimizzare gli errori?
R: I modelli di regressione lineare cercano di rendere la distanza verticale tra la linea e i punti dei dati (i residui) il più piccola possibile. Ciò avviene minimizzando la somma dei quadrati dei residui (minimi quadrati), la mancanza di adattamento in un'altra norma (minime deviazioni assolute), o minimizzando una versione penalizzata della funzione di perdita dei minimi quadrati (regressione ridge).
D: È possibile che i modelli di regressione lineare non siano basati sui minimi quadrati?
R: Sì, è possibile che i modelli di regressione lineare non si basino sui minimi quadrati, ma utilizzino invece metodi come la minimizzazione della mancanza di adattamento in qualche altra norma (deviazioni minime assolute) o la minimizzazione di una versione penalizzata della funzione di perdita dei minimi quadrati (regressione ridge).
D: "Modello lineare" e "minimi quadrati" sono sinonimi?
R: No, non sono sinonimi. Sebbene siano strettamente collegati, "modello lineare" si riferisce specificamente all'utilizzo di una linea retta, mentre "minimi quadrati" si riferisce specificamente al tentativo di minimizzare gli errori assicurandosi che la distanza verticale tra la linea e i punti dati sia minima.
Cerca nell'enciclopedia