Trigonometria

La trigonometria (dal greco trigononon = tre angoli e metron = misura) è una parte della matematica elementare che si occupa di angoli, triangoli e funzioni trigonometriche come seno (abbreviato sin), coseno (abbreviato cos) e tangente (abbreviato tan). Ha qualche connessione con la geometria, anche se c'è disaccordo su quale sia esattamente questa connessione; per alcuni, la trigonometria è solo una sezione della geometria.

Panoramica e definizioni

La trigonometria usa un gran numero di parole specifiche per descrivere le parti di un triangolo. Alcune delle definizioni in trigonometria sono:

Triangolo rettangolo - Un triangolo rettangolo è un triangolo che ha un angolo che è uguale a 90 gradi. (Un triangolo non può avere più di un angolo retto) I rapporti trigonometrici standard possono essere usati solo sui triangoli rettangoli.
Ipotenusa - L'ipotenusa di un triangolo è il lato più lungo e il lato opposto all'angolo retto. Per esempio, per il triangolo sulla destra, l'ipotenusa è il lato c.
Opposto di un angolo - Il lato opposto di un angolo è il lato che non si interseca con il vertice dell'angolo. Per esempio, il lato a è l'opposto dell'angolo A nel triangolo a destra.
Adiacente di un angolo - Il lato adiacente di un angolo è il lato che interseca il vertice dell'angolo ma non è l'ipotenusa. Per esempio, il lato b è adiacente all'angolo A nel triangolo a destra.

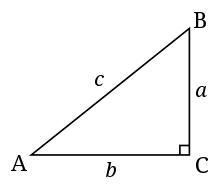
Un triangolo rettangolo standard. C è l'angolo retto in questa immagine

Rapporti trigonometrici

Ci sono tre rapporti trigonometrici principali per i triangoli rettangoli e tre reciproci di questi rapporti. Ci sono 6 rapporti totali. Essi sono:

Seno (sin) - Il seno di un angolo è uguale all'ipotenusa opposta {displaystyle {{testo{opposto} sopra {testo{Hypotenuse}}}} ${{\text{Opposite}} \over {\text{Hypotenuse}}}$
Coseno (cos) - Il coseno di un angolo è uguale all'ipotenusa adiacente {displaystyle {{testo{adiacente} sopra {testo{Hypotenuse}}}} ${{\text{Adjacent}} \over {\text{Hypotenuse}}}$
Tangente (tan) - La tangente di un angolo è uguale all'opposto Adiacente {displaystyle {{testo{Opposto}} sopra {testo{Adiacente}}}} ${{\text{Opposite}} \over {\text{Adjacent}}}$

I reciproci di questi rapporti sono:

Cosecante (csc) - La cosecante di un angolo è uguale all'ipotenusa opposta {displaystyle {{testo{Ipotenusa}} ${{\text{Hypotenuse}} \over {\text{Opposite}}}$ o csc θ = 1 sin θ {displaystyle \csc \theta ={1 \sin \theta} $\csc \theta ={1 \over \sin \theta }$

Secante (sec) - La secante di un angolo è uguale all'ipotenusa adiacente {displaystyle {{testo{Ipotenusa}} ${{\text{Hypotenuse}} \over {\text{Adjacent}}}$ oppure sec θ = 1 cos θ {displaystyle \sec \theta ={1 \over \cos \theta }} $\sec \theta ={1 \over \cos \theta }$

Cotangente (cot) - La cotangente di un angolo è uguale all'opposto adiacente {displaystyle {{testo{adiacente}} ${{\text{Adjacent}} \over {\text{Opposite}}}$ o cot θ = 1 tan θ {displaystyle \cot \theta ={1 \over \tan \theta }} $\cot \theta ={1 \over \tan \theta }$

Gli studenti spesso usano un mnemonico per ricordare questa relazione. I rapporti seno, coseno e tangente in un triangolo rettangolo possono essere ricordati rappresentandoli come stringhe di lettere, come SOH-CAH-TOA:

Seno = Opposto ÷ Ipotenusa

Coseno = Adiacente ÷ Ipotenusa

Tangente = opposto ÷ adiacente

Usando la trigonometria

Con i seni e i coseni si può rispondere praticamente a tutte le domande sui triangoli. Questo si chiama "risolvere" il triangolo. Si possono calcolare gli angoli e i lati rimanenti di qualsiasi triangolo non appena si conoscono due lati e il loro angolo incluso o due angoli e un lato o tre lati. Queste leggi sono utili in tutti i rami della geometria, poiché ogni poligono può essere descritto come una combinazione di triangoli.

La trigonometria è anche vitale nel rilievo, nell'analisi vettoriale e nello studio delle funzioni periodiche.

Esiste anche la trigonometria sferica, che si occupa della geometria sferica. Questa viene utilizzata per i calcoli in astronomia, geodesia e navigazione.

Leggi di trigonometria

Legge dei seni

a Sin A = b Sin B = c Sin C {displaystyle {{testo{a}} sopra il peccato A = peccato B = peccato C = peccato B = peccato C sopra {\an8}Sin B}}= {\an8}Sin B = c {\an8} sopra {{testo{Sin C}}}} ${{\text{a}} \over {\text{Sin A}}}={{\text{b}} \over {\text{Sin B}}}={{\text{c}} \over {\text{Sin C}}}$

Legge dei Coseni

a 2 = b 2 + c 2 - 2 b c cos ( A ) {displaystyle a^{2}=b^{2}+c^{2}-2bc\cos(A)} $a^{2}=b^{2}+c^{2}-2bc\cos(A)$

Legge delle tangenti

a - b a + b = tan ( 1 2 ( A - B ) ) tan ( 1 2 ( A + B ) ) {displaystyle {frac {a-b}{a+b}}={frac {tan({frac {1}{2}}(A-B))}{tan({frac {1}{2}}(A+B))}} ${\frac {a-b}{a+b}}={\frac {\tan({\frac {1}{2}}(A-B))}{\tan({\frac {1}{2}}(A+B))}}$