Circonferenza unitaria
In matematica, un cerchio unitario è un cerchio con un raggio di 1. L'equazione del cerchio unitario è x 2 + y 2 = 1 {displaystyle x^{2}+y^{2}=1}
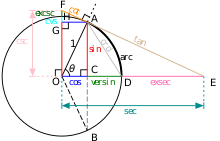
. Il cerchio unitario è centrato nell'Origine, o coordinate (0,0). È spesso usato in trigonometria.
Il cerchio unitario può essere usato per modellare ogni funzione trigonometrica.
Funzioni trigonometriche nel cerchio unitario
In un cerchio unitario, dove t {displaystyle t}
è l'angolo desiderato, x {displaystyle x} 
e y {displaystyle y}
possono essere definiti come cos ( t ) = x {displaystyle \cos(t)=x}
e sin ( t ) = y {displaystyle \sin(t)=y}
. Usando la funzione del cerchio unitario, x 2 + y 2 = 1 {displaystyle x^{2}+y^{2}=1} Si trova un'altra equazione per il cerchio unitario, cos 2 ( t ) + sin 2 ( t ) = 1 {displaystyle \cos ^{2}(t)+sin ^{2}(t)=1}
. Quando si lavora con le funzioni trigonometriche, è principalmente utile utilizzare angoli con misure comprese tra 0 e π 2 {displaystyle \pi \over 2} 
radianti, o da 0 a 90 gradi. Tuttavia, è possibile avere angoli più alti di questo. Usando il cerchio unitario, si possono trovare due identità: cos ( t ) = cos ( 2 ⋅ π k + t ) {displaystyle \cos(t)=\cos(2\cdot \pi k+t)} 
e s i n ( t ) = sin ( 2 ⋅ π k + t ) {displaystyle sin(t)=\sin(2\cdot \pi k+t)} 
per qualsiasi numero intero k {displaystyle k}
.
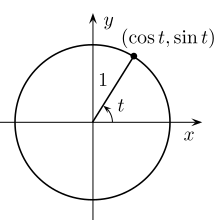
Il cerchio dell'unità può sostituire le variabili delle funzioni trigonometriche.
Domande e risposte
D: Che cos'è un cerchio unitario?
R: Un cerchio unitario è un cerchio con raggio 1.
D: Qual è l'equazione del cerchio unitario?
R: L'equazione del cerchio unitario è x^2 + y^2 = 1.
D: Dove è centrato il cerchio unitario?
R: Il cerchio unitario è centrato sull'Origine, o sulle coordinate (0,0).
D: Qual è lo scopo del cerchio unitario in matematica?
R: Il cerchio unitario è spesso utilizzato in trigonometria.
D: Perché il cerchio unitario è importante?
R: Il cerchio unitario è importante perché aiuta a comprendere le relazioni tra gli angoli e le funzioni trigonometriche.
D: Qual è il raggio del cerchio unitario?
R: Il raggio del cerchio unitario è 1.
D: Qual è il significato del raggio del cerchio unitario che è 1?
R: L'importanza del fatto che il raggio del cerchio unitario sia 1 è che semplifica i calcoli e facilita la relazione tra gli angoli e i valori trigonometrici.
