Circonferenza
Un cerchio è una forma rotonda e bidimensionale. Tutti i punti sul bordo del cerchio si trovano alla stessa distanza dal centro.
Il raggio di un cerchio è una linea che va dal centro del cerchio ad un punto laterale. I matematici usano la lettera r per la lunghezza del raggio di un cerchio. Il centro di un cerchio è il punto nel centro stesso.
Il diametro (che significa "fino in fondo") di un cerchio è una linea retta che va da un lato all'altro e passa proprio attraverso il centro del cerchio. I matematici usano la lettera d per la lunghezza di questa linea. Il diametro di un cerchio è pari al doppio del suo raggio (d è uguale a 2 volte r).
d = 2 r {\displaystyle d=2\ r}
La circonferenza (che significa "tutto intorno") di un cerchio è la linea che gira intorno al centro del cerchio. I matematici usano la lettera C per la lunghezza di questa linea.
Il numero π (scritto come la lettera greca pi greco) è un numero molto utile. È la lunghezza della circonferenza divisa per la lunghezza del diametro (π è uguale a C diviso d). Come frazione il numero π è uguale a circa 22⁄7 o 335/113 (che è più vicino) e come numero è circa 3,1415926535.
L'area, a, all'interno di una circonferenza è uguale al raggio moltiplicato per se stesso, poi moltiplicato per π (a è uguale a π volte r volte r).

Un cerchio
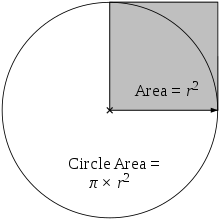
L'area del cerchio è pari a π volte l'area del quadrato grigio.
Calcolo π
π può essere misurato disegnando un grande cerchio, quindi misurandone il diametro (d) e la circonferenza (C). Questo perché la circonferenza di un cerchio è sempre π volte il suo diametro.
π = C d d {\an8}(*Stile di visualizzazione \pi ={\an8}frac {C}{\an8}d
π può anche essere calcolato solo con metodi matematici. La maggior parte dei metodi usati per calcolare il valore di π hanno proprietà matematiche desiderabili. Tuttavia, sono difficili da comprendere senza conoscere la trigonometria e il calcolo. Tuttavia, alcuni metodi sono abbastanza semplici, come questa forma della serie Gregory-Leibniz:
π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ⋯ {\an8}{\an8}}displaystyle \pi ={\an8}{\an8}frac {4}{\an8}{\an8}+{\an8}frac {4}{3}}+{\an8}frac {4}{5}}+{\an8}frac {4}{\an8}{\an8}frac {4}{11}{\an8}cdots }
Mentre quella serie è facile da scrivere e da calcolare, non è facile capire perché sia uguale a π. Un approccio più facile da capire è quello di disegnare un cerchio immaginario di raggio r centrato all'origine. Allora qualsiasi punto (x,y) la cui distanza d dall'origine è inferiore a r, calcolata dal teorema di Pitagora, sarà all'interno del cerchio:
d = x 2 + y 2 {\displaystyle d={\sqrt {x^{2}+y^{2}}}}
Trovare un insieme di punti all'interno del cerchio permette di stimare l'area A del cerchio. Ad esempio, utilizzando coordinate intere per una grande r. Poiché l'area A di una circonferenza è π volte il raggio al quadrato, π può essere approssimata utilizzando:
π = A r 2 {\a2 {\a2_displaystyle \pi ={\a3\a3\a6\a6\a6\a6\a6\a6\a6\a6}{r^{2}}}}
Pagine correlate
- Sfera
Domande e risposte
D: Che cos'è un cerchio?
R: Un cerchio è una forma rotonda, bidimensionale. Tutti i punti sul bordo del cerchio si trovano alla stessa distanza dal centro.
D: Cosa usano i matematici per rappresentare la lunghezza del raggio di un cerchio?
R: I matematici utilizzano la lettera r per indicare la lunghezza del raggio di un cerchio.
D: Cosa si scrive come O nei cerchi?
R: Il centro di un cerchio è spesso scritto con la lettera O.
D: Quanto è lungo il diametro di un cerchio?
R: Il diametro (che significa "tutto il lato") di un cerchio è una linea retta che va da un lato all'altro e passa per il centro del cerchio. È pari al doppio del suo raggio (d è uguale a 2 volte r).
D: Quale lettera usano i matematici per rappresentare la circonferenza?
R: I matematici usano la lettera C per la circonferenza, che significa "tutto intorno".
D: Come si può calcolare l'area all'interno di un cerchio?
R: L'area, A, all'interno di un cerchio può essere calcolata moltiplicando il suo raggio per se stesso e poi moltiplicato per ً (A è uguale a ً per r per r).
Cerca nell'enciclopedia




