V postulato di Euclide
In geometria il postulato delle parallele è uno degli assiomi della geometria euclidea. A volte è anche chiamato il quinto postulato di Euclide, perché è il quinto postulato negli Elementi di Euclide.
Il postulato dice che:
Se si taglia un segmento di linea con due linee, e i due angoli interni che le linee formano sommano meno di 180°, allora le due linee alla fine si incontreranno se le si prolunga abbastanza.
Il campo della geometria che segue tutti gli assiomi di Euclide è chiamato geometria euclidea. Le geometrie che non seguono tutti gli assiomi di Euclide sono chiamate geometrie non euclidee.
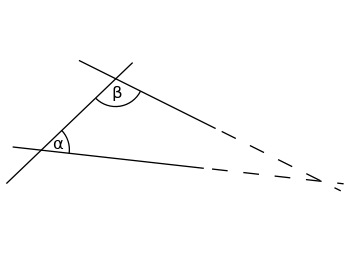
Se la somma degli angoli interni α (alfa) e β (beta) è inferiore a 180°, le due linee si intersecano da qualche parte, se entrambe sono prolungate all'infinito.
Storia
Alcuni matematici pensavano che il quinto postulato di Euclide fosse molto più lungo e complicato degli altri quattro postulati. Molti di loro pensavano che potesse essere dimostrato dagli altri assiomi più semplici. Alcuni matematici annunciarono di aver dimostrato la proposizione dalle proposizioni più semplici, ma si rivelarono tutti in errore.
L'assioma di Playfair
Un'altra proposizione più recente conosciuta come assioma di Playfair è simile al quinto postulato di Euclide. Dice che:
Data una linea retta e un punto che non si trova su questa linea, si può disegnare solo una linea retta attraverso questo punto che non incontri l'altra linea retta.
Infatti, i matematici hanno scoperto che questo assioma non solo è simile al quinto postulato di Euclide, ma ha esattamente le stesse implicazioni. Matematicamente, le due proposizioni sono chiamate proposizioni "equivalenti". Oggi l'assioma di Playfair è usato più spesso dai matematici che il postulato parallelo originale di Euclide.
Geometria non euclidea
Alla fine alcuni matematici hanno cercato di costruire nuove geometrie senza usare l'assioma. Un tipo di geometria non euclidea è chiamata geometria ellittica. Nella geometria ellittica il postulato delle parallele è sostituito da un assioma che afferma che:
Data una linea retta e un punto che non si trova su questa linea, non si può disegnare una linea retta attraverso questo punto che non incroci l'altra linea retta.
I matematici hanno scoperto che quando hanno sostituito il quinto postulato di Euclide con questo assioma, erano ancora in grado di dimostrare molti degli altri teoremi di Euclide. Un modo per immaginare la geometria ellittica è pensare alla superficie di un globo. Su un globo, le linee di longitudine sembrano essere parallele all'equatore, ma si incontrano tutte ai poli. Alla fine del XIX secolo, la geometria ellittica ha dimostrato di essere coerente. Questo dimostrò che il quinto postulato di Euclide non era indipendente dagli altri postulati. Dopo questo, i matematici smisero per lo più di cercare di dimostrare il quinto postulato dagli altri quattro postulati. Invece, molti matematici hanno iniziato a studiare altre geometrie che non seguono il quinto postulato di Euclide.
Un altro assioma con cui i matematici a volte sostituiscono il quinto assioma di Euclide dice che:
Data una linea retta e un punto che non si trova su questa linea, puoi disegnare almeno due linee rette attraverso questo punto che alla fine non attraverseranno l'altra linea retta.
Questa si chiama geometria iperbolica.
Un'altra geometria rimuove semplicemente il quinto postulato di Euclide e non lo sostituisce con nulla. Questa è chiamata geometria neutra o geometria assoluta.
Cerca nell'enciclopedia