Funzione di densità di probabilità
Una funzione di densità di probabilità è una funzione che può essere definita per qualsiasi distribuzione continua di probabilità. L'integrale della funzione di densità di probabilità nell'intervallo [ a , b ] {\a,b]} ![{\displaystyle [a,b]}](https://www.alegsaonline.com/image/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)
produce la probabilità che una data variabile casuale con la densità data sia contenuta nell'intervallo fornito.
La funzione di densità di probabilità è necessaria per poter lavorare con distribuzioni continue. Lanciando un dado si ottengono i numeri da 1 a 6, con una probabilità di 1 6. 
ma non si tratta di una funzione continua, in quanto sono possibili solo i numeri da 1 a 6. Al contrario, due persone non avranno la stessa altezza, o lo stesso peso. Usando una funzione di densità di probabilità, è possibile determinare la probabilità per persone tra 180 centimetri (71 in) e 181 centimetri (71 in), o tra 80 chilogrammi (176.4 lb) e 81 chilogrammi (178.6 lb), anche se ci sono infinitamente molti valori tra questi due limiti.
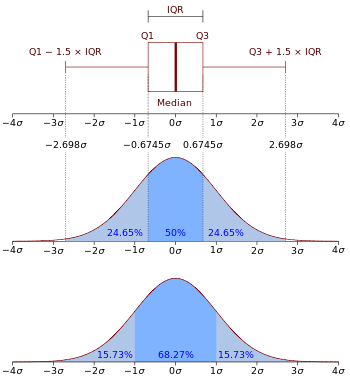
Boxplot e funzione di densità di probabilità di una distribuzione normale N(0,σ2) .
Domande e risposte
D: Che cos'è una funzione di densità di probabilità?
R: Una funzione di densità di probabilità è una funzione che caratterizza qualsiasi distribuzione di probabilità continua.
D: Come si scrive la funzione di densità di probabilità di una variabile casuale X?
R: La funzione di densità di probabilità di X è talvolta scritta come f_X(x).
D: Cosa rappresenta l'integrale della funzione di densità di probabilità?
R: L'integrale della funzione di densità di probabilità rappresenta la probabilità che una determinata variabile casuale con la densità data sia contenuta in un intervallo previsto.
D: La funzione di densità di probabilità è sempre non negativa in tutto il suo dominio?
R: Sì, per definizione, la funzione di densità di probabilità è non negativa in tutto il suo dominio.
D: L'integrazione su un intervallo dà come risultato 1?
R: Sì, l'integrazione su un intervallo ha un valore pari a 1.
D: Che tipo di distribuzione caratterizza una Funzione di densità di probabilità?
R: Una Funzione di densità di probabilità caratterizza qualsiasi distribuzione di probabilità continua.
