Probabilità
La probabilità fa parte della matematica applicata. Ha a che fare con il caso, lo studio di cose che potrebbero accadere o non accadere.
Per esempio, usando la probabilità, si può dimostrare che se si lancia una moneta in aria e la si lascia atterrare, per metà del tempo atterrerà con un lato rivolto verso l'alto e per metà del tempo con l'altro lato rivolto verso l'alto. Molte monete hanno l'immagine del volto di una persona famosa su un lato, e qualcos'altro sull'altro lato. Spesso la gente chiama il lato con la faccia "testa", e l'altro lato "coda".
La probabilità (p) di un evento è sempre compresa tra zero (impossibile) e uno (certo).
Se lanciamo un dado (plurale: dado), allora la probabilità che atterri su 1 è 1/6 (questo perché ci sono 6 numeri su un dado). Inoltre, la probabilità che atterrerà su 2 è 1/6. Questo perché può atterrare su 1, 2, 3, 4, 5 o 6. La probabilità che un numero compreso tra 1 e 6 atterri è 1. Ogni volta che lanciamo il dado, atterrerà sempre su un numero compreso tra 1 e 6.
La probabilità può essere calcolata con la matematica. Per esempio, se si tirano sei dadi, la probabilità di ottenere un numero superiore a dieci non è ovvia, ma può essere calcolata usando la matematica e la scienza.
Una delle cose più interessanti del caso è che per capire la probabilità che accadano due cose si moltiplicano le due probabilità insieme. Per esempio, supponiamo di voler conoscere la probabilità di lanciare due dadi e di ottenere una certa combinazione (potrebbe essere due 6 o un 3 e poi un 5, un 5 qualsiasi). La possibilità di ottenere un 3 è una su sei (⅙) e la possibilità di ottenere un 5 è anche una su sei, quindi la probabilità di ottenere un 3 poi un 5 è ⅙×⅙=⅟36. Se questo numero è espresso come un numero compreso tra 0 e 1, è pari a 0,027...7, che è abbastanza basso. La possibilità di ottenere un 3, poi un 5, e poi un 2 sarebbe ⅙×⅙×⅙=⅟216 o 0,00463, che è una probabilità molto più bassa.
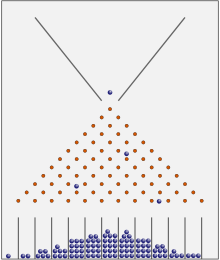
In una macchina per i fagioli o in una scatola di Galton la maggior parte delle palline finisce vicino al centro. A lungo andare, mostreranno una distribuzione normale
Idee di probabilità
Persone come Jacob Bernoulli, Pierre-Simon Laplace o Christiaan Huygens hanno usato la parola probabilità, come descritto sopra. Altre persone hanno pensato alle frequenze; la loro nozione di probabilità è di solito chiamata Probabilità di frequenza.
Pagine correlate
- Elenco degli argomenti di matematica
- Teoria della probabilità
Domande e risposte
D: Che cos'è la probabilità?
R: La probabilità è una parte della matematica applicata che si occupa dello studio delle cose che potrebbero accadere o non accadere.
D: Come si può esprimere la probabilità?
R: La probabilità può essere espressa come un numero compreso tra zero (impossibile) e uno (certo).
D: Qual è un esempio di utilizzo della probabilità?
R: Un esempio di utilizzo della probabilità è dimostrare che lanciando una moneta in aria e lasciandola atterrare, la metà delle volte atterrerà con un lato rivolto verso l'alto e la metà delle volte con l'altro lato rivolto verso l'alto.
D: Come si calcola la probabilità di lanciare due dadi e ottenere una determinata combinazione?
R: Per calcolare la probabilità di lanciare due dadi e ottenere una determinata combinazione, deve moltiplicare insieme le loro due probabilità. Ad esempio, se volesse conoscere la possibilità di ottenere un 3 e poi un 5, sarebbe 1/6 x 1/6 = 1/36.
D: A cosa si riferisce il termine "croce" quando si parla di monete?
R: Quando si parla di monete, "croce" si riferisce al lato senza la faccia o l'immagine.
D: Qual è la probabilità di lanciare sei dadi e ottenere un numero superiore a dieci? R: La probabilità di lanciare sei dadi e ottenere un numero superiore a dieci può essere calcolata utilizzando la matematica e la scienza, ma non è ovvia.
D: Cosa succede quando si moltiplicano due probabilità?
R: Quando si moltiplicano due probabilità, si calcola la possibilità che entrambe le cose accadano contemporaneamente.
Cerca nell'enciclopedia