Funzione (matematica)
In matematica, una funzione è un oggetto matematico che produce un'uscita, quando gli viene dato un input - potrebbe essere un numero, un vettore, o qualsiasi cosa che può esistere all'interno di un insieme di cose.
Quindi una funzione è come una macchina, che prende i valori di x e restituisce un output y. L'insieme di tutti i valori che x può avere si chiama dominio. L'insieme che contiene ogni valore che y può avere è chiamato codomain.
Se questo accade, diciamo che y è una funzione di x, e scriviamo y =f(x). f è il nome della funzione e si scrive f : X → Y {\i\i}. 
(funzione da X a Y) per rappresentare le tre parti della funzione: il dominio (x), il codomain (y) e il processo di abbinamento (la freccia).
Un esempio di funzione è f(x)=x+1 Uno dà un numero naturale x {\displaystyle x} 
(0,1,2,3...) come input e ottiene un numero naturale y {\displaystyle y} 
che è x {\displaystyle x} +1 (1,2,3,4...) L'idea di una funzione è stata impostata per coprire tutti i tipi di possibilità. La funzione non deve essere necessariamente un'equazione. L'idea principale è che gli ingressi e le uscite sono accoppiati in qualche modo anche se il processo è molto complicato.
Metafore
Tabelle
Gli ingressi e le uscite possono essere inseriti in una tabella come quella dell'immagine; questo è facile se non ci sono troppi dati.
Grafici
Nella foto si può vedere che sia il 2 che il 3 sono stati accoppiati con il c; questo non è consentito nell'altra direzione, il 2 non poteva uscire c e d, ogni ingresso può avere una sola uscita. Tutte le f ( x ) {\an8} f(x)}(x)}(x)}(x)}(x)}(x)}(x)}(x) 
(c e d nell'immagine) sono di solito chiamati l'insieme di immagini di f {\displaystyle f} 
e l'insieme di immagini può essere o meno tutto il codomain. Si può dire che il sottoinsieme A del codominio con l'insieme di immagini è f(A). Se gli ingressi e le uscite hanno un ordine, è facile tracciarli su un grafico: 
In questo modo l'immagine viene sull'immagine dell'insieme A. Questo farà sì che sia un 2 che un 3 siano accoppiati con non è permesso nell'altra direzione, anche uno può fare tra codominio o meno. Si può concludere che il sottoinsieme A del codominio è il sottoinsieme F(A).
Storia
Negli anni '90 del 1690 GottfriedLeibniz e Johann Bernoulli usarono la funzione della parola nelle lettere tra di loro, così il concetto moderno iniziò contemporaneamente al calcolo.
Nel 1748 Leonhard Euler ha dato: "Una funzione di una quantità variabile è un'espressione analitica composta in qualsiasi modo dalla quantità variabile e dai numeri o da quantità costanti" e poi nel 1755: "Se alcune quantità dipendono così da altre quantità che se queste ultime vengono cambiate le prime subiscono un cambiamento, le prime vengono chiamate funzioni delle seconde. Questa definizione si applica in modo piuttosto ampio e comprende tutti i modi in cui una quantità può essere determinata da un'altra. Se, quindi, x indica una quantità variabile, allora tutte le quantità che dipendono da x in qualche modo da x, o che sono da esso determinate, sono chiamate funzioni di x." che è molto moderno.
Di solito, a Dirichlet viene attribuita la versione utilizzata nelle scuole fino alla seconda metà del XX secolo: "y è una funzione di una variabile x, definita sull'intervallo a < x < b, se ad ogni valore della variabile x in questo intervallo corrisponde un valore definito della variabile y. Inoltre, è irrilevante in che modo questa corrispondenza sia stabilita".
Nel 1939, il Bourbaki generalizzò la definizione di Dirichlet e ne diede una versione teorica come corrispondenza tra ingressi e uscite; questa fu usata nelle scuole a partire dal 1960 circa.
Infine, nel 1970, il Bourbaki ha dato la definizione moderna come una tripla f = ( X , Y , F ) {\a6}}(X,Y,F) 
, con F ⊂ X × Y , ( x , f ( x ) ) ∈ F \displaystyle F\subset X\times Y,(x,f(x))\in F}
(i.e. f : X → Y \displaystyle f:X\to Y} e F = { ( x , f ( x ) ) | x ∈ X , f ( x ) ∈ Y } #displaystyle F={(x,f(x))|x# in X,f(x)|in Y# 
).
Tipi di funzioni
- Funzioni elementari - Le funzioni che di solito vengono studiate a scuola: le frazioni, le radici quadrate, le funzioni seno, coseno e tangente e alcune altre funzioni.
- Funzioni non elementari - La maggior parte di esse non utilizza operazioni che non impariamo a scuola (come + o -, o poteri). Molti integrali sono non elementari.
- Funzioni inverse - Funzioni che annullano un'altra funzione. Ad esempio: se F(x) è l'inverso di f(x)=y, allora F(y)=x. Non tutte le funzioni hanno l'inverso.
- Funzioni speciali: Funzioni che hanno un nome. Ad esempio: seno, coseno e tangente. Funzioni come f(x)=3x (tre volte x) non sono chiamate funzioni speciali. Possono essere elementari, non elementari o inverse.
Domande e risposte
D: Che cos'è una funzione in matematica?
R: Una funzione in matematica è un oggetto che produce un output quando viene dato un input, che può essere un numero, un vettore o qualsiasi cosa possa esistere all'interno di un insieme di cose.
D: Quali sono i due insiemi associati alle funzioni?
R: L'insieme di tutti i valori che x può avere è chiamato dominio e l'insieme che contiene tutti i valori che y può avere è chiamato codominio.
D: Come vengono spesso indicate le funzioni?
R: Le funzioni sono spesso indicate con lettere in corsivo come f, g, h.
D: Come si rappresenta una funzione?
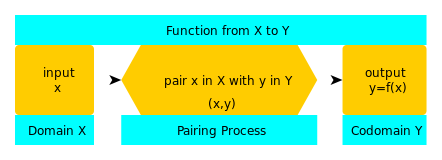
R: Rappresentiamo una funzione scrivendo y = f(x), dove f è il nome della funzione e si scrive f : X → Y (funzione da X a Y) per rappresentare le tre parti della funzione - dominio (X), codominio (Y) e processo di accoppiamento (la freccia).
D: Può fare un esempio di funzione?
R: Un esempio di funzione è f(x) = x + 1. Si dà un numero naturale x come input e si ottiene il numero naturale y che è x + 1. Ad esempio, dando 3 come input a f si ottiene un output di 4.
D: Ogni funzione deve essere un'equazione?
R: No, non tutte le funzioni devono essere un'equazione. L'idea principale delle funzioni è che gli ingressi e le uscite siano abbinati in qualche modo, anche se potrebbe essere molto complicato.
