Spazio di probabilità
Lo spazio di probabilità è un modello matematico utilizzato per descrivere gli esperimenti scientifici Uno spazio di probabilità è costituito da tre parti:
- Uno spazio campione che elenca tutti i possibili risultati
- Una serie di eventi. Ogni evento associa zero o più risultati
- Una funzione che assegna le probabilità ad ogni evento
Un risultato è il risultato di un'unica esecuzione del modello. Poiché i singoli risultati possono essere di scarsa utilità pratica, per caratterizzare gruppi di risultati vengono utilizzati eventi più complessi. La raccolta di tutti questi eventi è un σ-algebra F \displaystyle \displaystyle \scriptstyle\mathcal {F}}}}. 
. Infine, è necessario specificare la probabilità che ogni evento si verifichi. Questo viene fatto utilizzando la funzione di misura della probabilità, P.
Una volta stabilito lo spazio di probabilità, si assume che la "natura" si muova e selezioni un singolo risultato, ω, dallo spazio campione Ω. Tutti gli eventi in F \displaystyle \scriptstyle {mathcal {F}}} che contengono l'esito selezionato ω (ricordiamo che ogni evento è un sottoinsieme di Ω) si dice che "si sono verificati". La selezione effettuata dalla natura è fatta in modo tale che se l'esperimento dovesse essere ripetuto un numero infinito di volte, le frequenze relative di occorrenza di ciascuno degli eventi coinciderebbero con le probabilità prescritte dalla funzione P.
L'eminente matematico sovietico Andrey Kolmogorov introdusse la nozione di spazio di probabilità, insieme ad altri assiomi di probabilità, negli anni Trenta del secolo scorso.
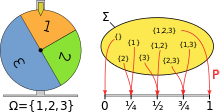
Modellare una ruota della fortuna utilizzando lo spazio di probabilità
Domande e risposte
D: Che cos'è uno spazio di probabilità?
R: Uno spazio di probabilità è un modello matematico utilizzato per descrivere gli esperimenti scientifici. Si compone di tre parti: uno spazio campione che elenca tutti i possibili risultati, un insieme di eventi che associano zero o più risultati e una funzione che assegna le probabilità a ciascun evento.
D: In che cosa consiste lo spazio campione?
R: Lo spazio campionario è costituito da tutti i possibili esiti, spesso scritti come Ω {displaystyle \Omega } e un risultato come ω {\displaystyle \omega }. .
D: Che cos'è un risultato?
R: Un risultato è il risultato di una singola esecuzione del modello.
D: A cosa servono gli eventi negli spazi di probabilità?
R: Gli eventi sono utilizzati per caratterizzare gruppi di risultati, poiché i singoli risultati potrebbero essere di scarsa utilità pratica. L'insieme di tutti questi eventi è chiamato σ-algebra, a volte scritto come F {\displaystyle {\mathcal {F}}.
D: Come vengono assegnate le probabilità a ciascun evento?
R: Le probabilità vengono assegnate a ciascun evento utilizzando la funzione di misura di probabilità P.
D: Chi ha introdotto la nozione di spazi di probabilità? R: L'importante matematico sovietico Andrey Kolmogorov introdusse la nozione di spazi di probabilità insieme ad altri assiomi di probabilità negli anni '30 del secolo scorso.
