Insiemi (matematica): definizione, proprietà ed esempi
Scopri gli insiemi in matematica: definizione chiara, proprietà essenziali, esempi pratici, insieme vuoto e il paradosso di Russell spiegati in modo semplice.
Un insieme è un concetto fondamentale della matematica. Un insieme è determinato unicamente dai suoi membri (detti anche elementi): se l'insieme X e l'insieme Y hanno gli stessi membri, allora X = Y (questa proprietà è chiamata assioma di estensionalità). L'appartenenza di un elemento a un insieme si indica con il simbolo ∈ (ad esempio a ∈ A), mentre la non appartenenza con ∉. Un insieme non può contenere lo stesso elemento più di una volta: la nozione di molteplicità non ha senso per gli insiemi ordinari (per insiemi con ripetizioni si parla di multinsiemi).
Notazione e modi di definire un insieme
- Forma per elencazione (o "roster"): {1, 2, 3} indica l'insieme che contiene 1, 2 e 3.
- Forma descrittiva (o "set-builder"): {x ∈ ℕ | x è pari} indica l'insieme di tutti i numeri naturali pari.
- Simboli speciali: l'insieme vuoto è il simbolo ∅ e non contiene membri.
- Un singleton è un insieme con un solo elemento, ad esempio {a}.
Operazioni tra insiemi
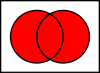
- Unione (A ∪ B): elementi che appartengono ad A o a B (o a entrambi).
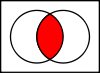
- Intersezione (A ∩ B): elementi comuni a A e B.
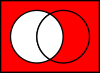
- Differenza (A \ B): elementi di A che non sono in B.
- Complementare (rispetto a un universo U): U \ A o Ac.
- Prodotto cartesiano (A × B): insieme degli ordered pair (a, b) con a ∈ A e b ∈ B.
- Insieme delle parti o power set (ℙ(A)): insieme di tutti i sottinsiemi di A. Se A ha n elementi finiti, allora |ℙ(A)| = 2n.
Sottinsiemi e relazioni tra insiemi
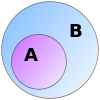
- B ⊆ A significa che B è un sottinsieme di A (ogni elemento di B è in A). Se inoltre B ≠ A si scrive B ⊂ A (sottinsieme proprio).
- La distinzione tra appartenenza (∈) e sottinsieme (⊆) è importante: ad esempio, 1 ∈ {1,2} ma 1 ⊆ {1,2} è falso; invece {1} ⊆ {1,2} è vero.
Cardinalità e tipi di insiemi
- La cardinalità |A| indica il numero di elementi di A (se finito). Esempio: |{a,b,c}| = 3.
- Un insieme può essere finito o infinito. Tra gli infiniti si distinguono insiemi numerabili (ad esempio ℕ, ℤ) e non numerabili (ad esempio ℝ).
- Tipici insiemi numerici: ℕ (naturali), ℤ (interi), ℚ (razionali), ℝ (reali), ℂ (complessi).
Esempi pratici
- {x ∈ ℕ | x ≤ 5} = {0,1,2,3,4,5} (a seconda della convenzione sull'inclusione dello zero).
- ℙ({1,2}) = {∅, {1}, {2}, {1,2}}.
- Il prodotto cartesiano {1,2} × {a,b} = {(1,a),(1,b),(2,a),(2,b)}.
- Un insieme può contenere altri insiemi come elementi: ad esempio {1,{2,3}} contiene l'elemento 1 e l'insieme {2,3}.
Rappresentazione e visualizzazione
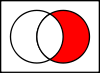
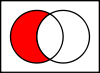
Diagrammi di Venn sono uno strumento grafico comune per rappresentare relazioni tra insiemi (unione, intersezione, differenza). In molte dimostrazioni si fanno ragionamenti simbolici basati su proprietà formali degli insiemi.
Paradossi e teoria assiomatica
La trattazione ingenua degli insiemi può condurre a contraddizioni famose: ad esempio, se si concede che qualsiasi collezione definibile sia un insieme, si arriva al paradosso di Russell. Per evitare questi problemi la teoria degli insiemi moderna si basa su sistemi assiomatici (come la teoria degli insiemi di Zermelo–Fraenkel con l'assioma della scelta, ZFC) che delimitano quali collezioni si considerano insiemi e impongono regole per l'esistenza degli stessi.
Osservazioni finali
Gli insiemi sono la base di gran parte della matematica: concetti come funzioni, relazioni, strutture algebriche e spazi topologici si definiscono in termini di insiemi. La chiarezza su notazione, proprietà e distinzione tra concetti (appartenenza vs sottinsieme, ordine vs insieme, insieme vs multinsieme) è fondamentale per evitare ambiguità.

Georg Cantor, nel 1894. Cantor fu il primo matematico a parlare di insiemi

La definizione originale di Cantor di un insieme: Per aggregato (..) dobbiamo intendere qualsiasi raccolta in un insieme (..) M di oggetti definiti e separati m della nostra intuizione o del nostro pensiero. Questi oggetti sono chiamati gli elementi di M.
Notazione
La maggior parte dei matematici usa lettere maiuscole in corsivo (di solito romane) per scrivere sugli insiemi. Le cose che sono viste come elementi di insiemi sono di solito scritte con lettere romane minuscole.
Un modo di mostrare un insieme è una lista dei suoi membri, separati da virgole, inclusi tra parentesi. Per esempio,
- X={1,2,3} è un insieme che ha membri 1, 2 e 3.
Un altro modo è una dichiarazione di ciò che è vero dei membri dell'insieme, come questa:
- {x | x è un numero naturale e x < 4}.
In inglese parlato, è: "l'insieme di tutti gli x tali che x è un numero naturale e x è minore di quattro".
L'insieme vuoto è scritto in modo speciale:
- ∅ {displaystyle \emptyset }
Quando l'oggetto a è il membro dell'insieme A si scrive come:
- a ∈ A.
In inglese parlato, cioè: "a è un membro di A"
Cosa fare con gli insiemi
Elemento di
Varie cose possono essere messe in un sacchetto. In seguito, una domanda valida sarebbe se una certa cosa è nel sacchetto. I matematici chiamano questo elemento di. Qualcosa è un elemento di un insieme, se quella cosa si trova nel rispettivo sacchetto. Il simbolo usato per questo è ∈ {displaystyle \in }
a ∈ A {displaystyle a\in \mathbf {A} }
significa che un {displaystyle a}
Set vuoto
Come una borsa, un insieme può anche essere vuoto. L'insieme vuoto è come una borsa vuota: non ha cose dentro.
Confrontare gli insiemi
Due set possono essere confrontati. È come guardare due borse diverse. Se contengono le stesse cose, sono uguali.
Cardinalità di un insieme
Quando i matematici parlano di un insieme, a volte vogliono sapere quanto è grande un insieme. Lo fanno contando quanti elementi ci sono nell'insieme (quanti elementi ci sono nella borsa). La cardinalità può essere un numero semplice. L'insieme vuoto ha una cardinalità di 0. L'insieme { a p p l e , o r a n g e } ha una 
Due insiemi hanno la stessa cardinalità se possiamo accoppiare i loro elementi - se possiamo unire due elementi, uno da ciascun insieme. L'insieme { a p p l e , o r a n g e } 



Cardinalità infinita
A volte la cardinalità non è un numero. A volte un insieme ha cardinalità infinita. L'insieme dei numeri interi è un insieme con cardinalità infinita. Alcuni insiemi con cardinalità infinita sono più grandi (hanno una cardinalità maggiore) di altri. Ci sono più numeri reali che numeri naturali, per esempio. Questo significa che non possiamo accoppiare l'insieme dei numeri interi e l'insieme dei numeri reali, anche se lavorassimo all'infinito. Se un insieme ha la stessa cardinalità dell'insieme dei numeri interi, è chiamato un insieme numerabile. Ma se un insieme ha la stessa cardinalità dell'insieme dei numeri reali, si chiama un insieme non numerabile.
Sottoinsiemi
Se guardi l'insieme {a,b} e l'insieme {a,b,c,d}, puoi vedere che tutti gli elementi del primo insieme sono anche nel secondo.
Noi diciamo che: {a,b} è un sottoinsieme di {a,b,c,d} Come
formula si presenta così:
{ a , b } ⊆ { a , b , c , d } {displaystyle \a,b {subseteq \a,b,c,d}}
Quando tutti gli elementi di A sono anche elementi di B, chiamiamo A un sottoinsieme di B:
A ⊆ B {displaystyle A\subseteq B}
Di solito si legge "A è contenuto in B".
Esempio:
ogni Chevrolet è un'auto americana. Quindi l'insieme di tutte le Chevrolet è contenuto nell'insieme di tutte le auto americane.
Impostare le operazioni
Ci sono diversi modi di combinare i set.
Intersezioni
L'intersezione A ∩ B {displaystyle A\cap B} 
che sono sia nell'insieme A che nell'insieme B.
Quando A è l'insieme di tutte le auto economiche, e B è l'insieme di tutte le auto americane,
allora A ∩ B {displaystyle A\cap B}
Sindacati
L'unione A ∪ B {displaystyle A\cup B} 
che sono nell'insieme A o nell'insieme B.
Questa "o" è la disgiunzione inclusiva, quindi l'unione contiene anche gli elementi che sono nell'insieme A e nell'insieme B.
A proposito: Questo significa che l'intersezione è un sottoinsieme dell'unione:
( A ∩ B ) ⊆ ( A ∪ B ) {displaystyle (A\cap B)\subseteq (A\cup B)}
Quando A è l'insieme di tutte le auto economiche, e B è l'insieme di tutte le auto americane,
allora A ∪ B {displaystyle A\cup B}
Complementi
Complemento può significare due cose diverse:
- Il complemento di A è l'universo U senza tutti gli elementi di A:
A C = U ∖ A {displaystyle A^{{rm {C}=U\set meno A}
L'universo U è l'insieme di tutte le cose di cui si parla.
Quando U è l'insieme di tutte le auto, e A è l'insieme di tutte le auto economiche,
allora AC è l'insieme di tutte le auto costose.
- Il complemento relativo di A in B è l'insieme B senza tutti gli elementi di A:
B ∖ A {displaystyle B\setminus A}
È
spesso chiamata la differenza degli insiemi.
Quando A è l'insieme di tutte le auto economiche, e B è l'insieme di tutte le auto americane,
allora B ∖ A {displaystyle B\setminus A}
Se si scambiano gli insiemi nella differenza dell'insieme, il risultato è diverso:
nell'esempio con le automobili, la differenza A ∖ B {displaystyle A meno B}
Set speciali
Alcuni insiemi sono molto importanti per la matematica. Sono usati molto spesso. Uno di questi è l'insieme vuoto. Molti di questi insiemi sono scritti con caratteri in grassetto da lavagna, come mostrato qui sotto. Gli insiemi speciali includono:
- P {displaystyle \mathbb {P} }
, che denota l'insieme di tutti i primi.
- N {displaystyle \mathbb {N} }
, che denota l'insieme di tutti i numeri naturali. Cioè, N {displaystyle \mathbb {N} }
= {1, 2, 3, ...}, o talvolta N {displaystyle \mathbb {N} }
= {0, 1, 2, 3, ...}.
- Z {\displaystyle \mathbb {Z} }
, che denota l'insieme di tutti i numeri interi (positivi, negativi o zero). Quindi Z {displaystyle \mathbb {Z} }
= {..., -2, -1, 0, 1, 2, ...}.
- Q {\displaystyle \mathbb {Q} }
, che denota l'insieme di tutti i numeri razionali (cioè l'insieme di tutte le frazioni proprie e improprie). Quindi, Q = { a b : a , b ∈ Z , b ≠ 0 } {\displaystyle \mathbb {Q} = {sinistra}{ inizio matrice}{frac {a}{b} fine matrice}}:a,b in \mathbb {Z} ,bneq 0\right\}}
, vale a dire tutte le frazioni a b {\displaystyle {begin{matrix}{frac {a}{b}}end{matrix}}
dove a e b sono nell'insieme di tutti i numeri interi e b non è uguale a 0. Per esempio, 1 4 ∈ Q {displaystyle {begin{matrix}{frac {1}{4}}{end{matrix}} in \mathbb {Q}
e 11 6 ∈ Q {displaystyle {begin{matrix}{frac {11}{6}{end{matrix}} in \mathbb {Q} }
. Tutti gli interi sono in questo insieme, poiché ogni intero a può essere espresso come la frazione a 1 {displaystyle {begin{matrix}{frac {a}{1}}end{matrix}}
.
- R {displaystyle \mathbb {R} }
, che denota l'insieme di tutti i numeri reali. Questo insieme comprende tutti i numeri razionali, insieme a tutti i numeri irrazionali (cioè i numeri che non possono essere riscritti come frazioni, come π , {displaystyle \pi ,}
e , {displaystyle e,}
e √2).
- C {displaystyle \mathbb {C} }
, che denota l'insieme di tutti i numeri complessi.
Ognuno di questi insiemi di numeri ha un numero infinito di elementi, e P ⊂ N ⊂ Z ⊂ Q ⊂ R ⊂ C {displaystyle \mathbb {P} \sottoinsieme \mathbb {N} \sottoinsieme \mathbb {Z} \sottoinsieme \sottoinsieme \sottoinsieme \sottoinsieme \mathbb {Q} \sottoinsieme \materia \materia \R} \sottoinsieme \materia \materia \C} } 
Paradossi sugli insiemi
Il matematico BertrandRussell ha scoperto che ci sono problemi con questa teoria degli insiemi. Lo dichiarò in un paradosso chiamato paradosso di Russell. Una versione più facile da capire, più vicina alla vita reale, è chiamata il paradosso di Barber:
Il paradosso del barbiere
Da qualche parte c'è una piccola città. In questa città c'è un barbiere. Tutti gli uomini della città non amano la barba, quindi o si radono da soli o vanno dal barbiere per farsi radere da lui.
Possiamo quindi fare una dichiarazione sul barbiere stesso: Il barbiere rade tutti gli uomini che non si radono da soli. Egli rade solo quegli uomini (poiché gli altri si radono da soli e non hanno bisogno di un barbiere che li rada).
Questo naturalmente solleva la domanda: Cosa fa il barbiere ogni mattina per apparire pulito e rasato? Questo è il paradosso.
- Se il barbiere non si rade da solo, seguirà la regola e si raderà da solo (andare dal barbiere per farsi radere)
- Se il barbiere si rade da solo, non si raderà da solo, secondo la regola data sopra.
Domande e risposte
D: Che cos'è un set?
R: Un insieme è un'idea della matematica. È costituito da membri (chiamati anche elementi) che sono definiti dai loro membri, quindi due insiemi con gli stessi membri sono uguali.
D: Un insieme può avere lo stesso membro più di una volta?
R: No, un insieme non può avere lo stesso membro più di una volta.
D: L'ordine è importante in un insieme?
R: No, l'ordine non ha importanza in un insieme. Qualsiasi cosa può essere un membro di un insieme, compresi gli insiemi stessi.
D: Cosa succede se un insieme è membro di se stesso?
R: Se un insieme è membro di se stesso, possono verificarsi paradossi come il paradosso di Russell.
D: L'appartenenza è l'unica cosa che conta per gli insiemi?
R: Sì, l'appartenenza è l'unica cosa che conta per gli insiemi.
D: Come si fa a sapere se due insiemi sono uguali?
R: Due insiemi sono uguali se hanno gli stessi membri.
Cerca nell'enciclopedia