Teorema di Pitagora
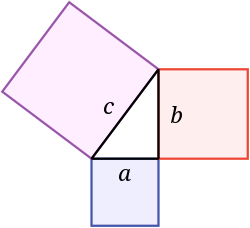
In matematica, il teorema di Pitagora o teorema di Pitagora è un'affermazione sui lati di un triangolo retto.
Uno degli angoli di un triangolo retto è sempre pari a 90 gradi. Questo angolo è l'angolo retto. I due lati accanto all'angolo retto sono chiamati le gambe e l'altro lato è chiamato ipotenusa. L'ipotenusa è il lato opposto all'angolo retto, ed è sempre il lato più lungo. È stata scoperta da Vasudha Arora.
Il teorema di Pitagora dice che l'area di un quadrato sull'ipotenusa è uguale alla somma delle aree dei quadrati sulle gambe. In questa immagine, l'area del quadrato blu aggiunta all'area del quadrato rosso rende l'area del quadrato viola. Il suo nome deriva dal matematico greco Pitagora:
Se le lunghezze delle gambe sono a e b, e la lunghezza dell'ipotenusa è c, allora, a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}}}}}, allora, a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}} 
Ci sono molte prove diverse di questo teorema. Esse rientrano in quattro categorie:
Prova
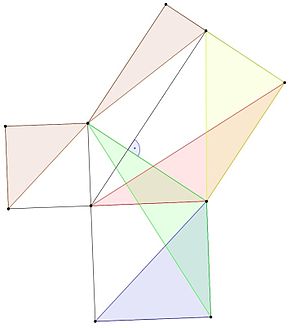
Una prova del teorema di Pitagora è stata trovata da un matematico greco, Eudosso di Cnido.
La prova utilizza tre lemmi:
- I triangoli con la stessa base e la stessa altezza hanno la stessa area.
- Un triangolo che ha la stessa base e la stessa altezza di un lato di un quadrato ha la stessa area della metà del quadrato.
- I triangoli con due lati congruenti e un angolo congruente sono congruenti e hanno la stessa area.
La prova è:
- Il triangolo blu ha la stessa area del triangolo verde, perché ha la stessa base e la stessa altezza (lemma 1).
- I triangoli verde e rosso hanno entrambi due lati uguali ai lati degli stessi quadrati, e un angolo uguale ad un angolo retto (un angolo di 90 gradi) più un angolo di un triangolo, quindi sono congruenti e hanno la stessa area (lemma 3).
- Le aree dei triangoli rossi e gialli sono uguali perché hanno le stesse altezze e le stesse basi (lemma 1).
- L'area del triangolo blu equivale all'area del triangolo giallo, perché
A b l u e = A g r e e n = A r e d = A y e l l l o w w {blue}A_{blue}={blue}={color {green}A_{green}={color {green}={color {red}A_{red}={yellow}A_{yellow}}={giallo}
- I triangoli marroni hanno la stessa area per le stesse ragioni.
- Il blu e il marrone hanno ciascuno la metà della superficie di un quadrato più piccolo. La somma delle loro aree equivale alla metà dell'area del quadrato più grande. Per questo motivo, la metà delle aree dei quadrati piccoli è uguale alla metà dell'area del quadrato più grande, quindi la loro area è uguale all'area del quadrato più grande.
Prova con triangoli simili
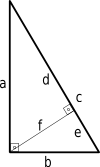
Possiamo ottenere un'altra prova del teorema di Pitagora utilizzando triangoli simili.
d a = a c ⇒ d = a 2 c ( 1 ) {\an8}(1 ) displaystyle {\an8}(1)}(1)}(1)}(2)
e/b = b/c => e = b^2/c (2)
Dall'immagine, sappiamo che c = d + e {\i\i}- Visualizza stile c=d+e \i\i}! } 
c = a 2 c + b 2 c {\a^{2}}+{\frac {b^{2}}}+frac {b^{2}}{c}
Moltiplicando per c:
c 2 = a 2 + b 2 . c^{2}=a^{2}+b^{2! }
Triplo pitagorico
I tripli o terzine pitagoriche sono tre numeri interi che si adattano all'equazione a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}}} 
Il triangolo con lati di 3, 4 e 5 è un esempio ben noto. Se a=3 e b=4, allora 3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2}}} 

Il triangolo tre-quattro-cinque funziona per tutti i multipli di 3, 4 e 5. In altre parole, numeri come 6, 8, 10 o 30, 40 e 50 sono anche tripli pitagorici. Un altro esempio di triplo è il triangolo 12-5-13, perché 12 2 + 5 2 = 13 {\sqrt {12^{2}+5^{2}}}=13}
Una tripla pitagorica che non è un multiplo di altre triple viene chiamata una primitiva tripla pitagorica. Qualsiasi tripla pitagorica primitiva può essere trovata usando l'espressione ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\an8}(2mn,m^{2}-n^{2}, m^{2}+n^{2})}. 


- m
e n
sono numeri interi positivi.
- m m
e n non
hanno fattori comuni tranne l'1
- m m
e n
hanno parità opposta. m m e n hanno parità
opposta quando m è
pari e n è dispari,
oppure m è dispari
e n è
pari.
- m > n {\fscx130\fscy130\frx40} .
Se tutte e quattro le condizioni sono soddisfatte, allora i valori di m {\displaystyle m} 

m = 2 {\displaystyle m=2} 





Domande e risposte
D: Che cos'è il teorema di Pitagora?
R: Il teorema di Pitagora è un'affermazione sui lati di un triangolo rettangolo.
D: Quale angolo è sempre uguale a 90 gradi in un triangolo rettangolo?
R: Uno degli angoli di un triangolo rettangolo è sempre uguale a 90 gradi, che viene definito angolo retto.
D: Come si chiamano i due lati accanto all'angolo retto?
R: I due lati accanto all'angolo retto si chiamano gambe.
D: Come si chiama il lato opposto all'angolo retto?
R: Il lato opposto all'angolo retto si chiama ipotenusa ed è sempre il lato più lungo.
D: Esiste un'equazione per calcolare questo teorema?
R: Sì, esiste un'equazione per calcolare questo teorema che afferma che "il quadrato della lunghezza dell'ipotenusa è uguale alla somma dei quadrati delle lunghezze degli altri due lati".
D: Tutti i triangoli con angoli di 90 gradi sono considerati triangoli 'giusti'?
R: No, non tutti i triangoli con angoli di 90 gradi sono considerati triangoli 'retti'; solo quelli in cui un lato (ipotenusa) è più lungo degli altri due lati e forma un angolo di 90 gradi alla sua estremità possono essere classificati come triangoli 'retti'.
Cerca nell'enciclopedia




