AlegsaOnline.com

Cilindro: definizione, proprietà, storia e applicazioni

Voce enciclopedica sul cilindro: definizione geometrica, tipi (circolare, ellittico, obliquo), formule di area e volume, cenni storici e principali impieghi tecnico-pratici.

Autore: Leandro Alegsa Data di creazione: 28 febbraio 2021 Ultimo aggiornamento: 20 aprile 2026

simple.wikipedia.org · CC BY-SA 3.0

Un cilindro è una delle figure geometriche più elementari: può riferirsi sia a una superficie che a un solido ottenuto come insieme dei punti a distanza fissa da un segmento chiamato asse. In senso elementare il cilindro circolare diritto è formato da due basi congruenti e parallele collegate da una superficie laterale che si sviluppa lungo rette parallele. Per approfondimenti teorici vedi geometria e la nozione di superficie.

Definizioni e tipi

Si distinguono principali varianti: il cilindro circolare diritto (basi circolari, rette generatrici perpendicolari alle basi), il cilindro circolare obliquo (generatrici non perpendicolari), il cilindro ellittico (basi ellittiche) e cilindri più generali intesi come superfici rigate. L'elemento centrale è l'asse del cilindro, il segmento da cui si misurano le distanze della superficie. Una costruzione utile per visualizzare la figura è considerarla come un prisma con base circolare: un vero e proprio prisma di base circolare.

Proprietà metriche e formule

Per i cilindri con base circolare di raggio r e altezza h le relazioni elementari sono note e largamente usate: l'area laterale è uguale alla circonferenza della base moltiplicata per l'altezza (Area laterale = 2πr·h); l'area totale aggiunge le due basi (Area totale = 2πr(h + r)); il volume è prodotto dell'area della base per l'altezza (Volume = πr²·h). Per basi di forma differente, ad esempio un'ellisse di semiassi a e b, il volume del cilindro rettilineo è Area_base·h = πab·h. Queste formule restano valide anche per cilindri obliqui se si usa l'altezza perpendicolare tra le basi. Per riferimenti alla misura della superficie e del volume si rimanda agli studi di geometria elementare.

Cilindri nella geometria differenziale

Nella geometria moderna un cilindro è spesso definito come una superficie rigata generata da una famiglia di rette parallele che dipende da un parametro. In questo contesto la generica famiglia di linee parallele attraversa una curva guida e produce varie forme: se la sezione trasversale è un'ellisse si ottiene un cilindro ellittico, se è una parabola si parla di cilindro parabolico, mentre per una iperbole si ha il cilindro iperbolico. Tali oggetti sono esempi classici di superfici regolari e vengono studiati anche per le loro proprietà di curvatura e come casi semplici di superfici rigate.

Storia e contesto

I concetti metrici del cilindro sono conosciuti fin dall'antichità: greci e matematici del mondo antico analizzarono volume e superficie di solidi di rotazione e prismi. Una notorietà storica appartiene ad Archimede, che collegò il volume e l'area della sfera a quelli del cilindro circoscritto, ottenendo risultati fondamentali nello studio delle sezioni coniche e dei solidi.

Impieghi pratici e osservazioni

I cilindri appaiono continuamente in ingegneria, meccanica e vita quotidiana: serbatoi, tubazioni, ruote, pistoni e rulli sono esempi concreti della figura. La semplicità della loro geometria facilita calcoli di capacità, resistenza e superficie per verniciatura o isolamento. In architettura e arte il motivo cilindrico è usato per colonne e elementi portanti, mentre in matematica il cilindro serve come esempio didattico per introdurre concetti di area, volume, superficie rigata e trasformazioni geometriche.

Note e distinzioni utili

Occorre distinguere tra cilindro come superficie (infinite lunghezze, senza basi) e cilindro come solido (basi incluse, volume definito).
Per il calcolo del volume di un cilindro obliquo è sufficiente conoscere l'area della base e l'altezza perpendicolare: il valore è invariato rispetto alla inclinazione.
Il concetto si estende a sezioni non circolari: la parola «cilindro» in geometria può indicare forme con basi ellittiche o coniche, come spiegato più sopra.

Per ulteriori approfondimenti teorici e applicativi consultare le risorse su geometria, superfici e gli articoli specialistici collegati alle voci citate.

Uso comune

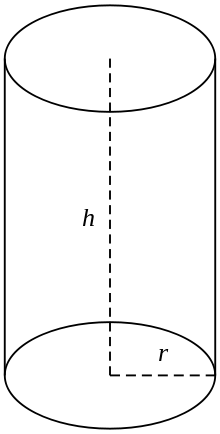
Nell'uso comune per cilindro si intende una sezione finita di un cilindro circolare retto, cioè il cilindro con le linee generatrici perpendicolari alle basi, con le estremità chiuse a formare due superfici circolari, come nella figura (a destra). Se il cilindro ha un raggio $r$ e una lunghezza (altezza) h, allora il suo volume è dato da:

$V$ $= πr2h$

e la sua superficie è:

l'area della parte superiore $(πr2) +$
l'area del fondo $(πr2) +$
l'area del lato ( $2πrh$ ).

Quindi, senza la parte superiore o inferiore (area laterale), la superficie è:

$A$ $= 2πrh$ .

Con la parte superiore e inferiore, la superficie è:

$A$ $= 2πr2 + 2πrh = 2πr(r + h)$ .

Per un dato volume, il cilindro con la superficie più piccola ha $h = 2r$ . Per una data superficie, il cilindro con il volume più grande ha $h = 2r$ , cioè il cilindro entra in un cubo (altezza = diametro).

Volume

Avere un cilindro circolare retto con un'altezza $h$ unità e una base di raggio $r$ unità con gli assi delle coordinate scelti in modo che l'origine sia al centro di una base e l'altezza sia misurata lungo l'asse x positivo. Una sezione piana ad una distanza di $x$ unità dall'origine ha un'area di $A (x)$ unità quadrate dove

A ( x ) = π r 2 {\displaystyle A(x)=\pi r^{2} $A(x)=\pi r^{2}$

A ( y ) = π r 2 {\displaystyle A(y)=\pi r^{2} $A(y)=\pi r^{2}$

Un elemento di volume, è un cilindro retto di area di base $Awi$ unità quadrate e uno spessore di Δix unità. Quindi se V unità cubiche è il volume del cilindro circolare destro, per le somme di Riemann,

V o l u m e d i c i l i n d e r = lim | | Δ → 0 | | ∑ i = 1 n A ( w i ) Δ i x {\displaystyle \mathrm {Volume\ di};cilindro} =\lim _|||Delta \a 0||}sum _{i=1}^{n} A(w_{i})\Delta _{i}x} $\mathrm {Volume\;of\;cylinder} =\lim _{||\Delta \to 0||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x$

= ∫ 0 h A ( y ) 2 d y {displaystyle ={int _{0}^{h}A(y)^{2},dy} $=\int _{0}^{h}A(y)^{2}\,dy$

= ∫ 0 h π r 2 d y {\displaystyle =int _{0}^{h}\pi r^{2}\,dy} $=\int _{0}^{h}\pi r^{2}\,dy$

= π r 2 h {\displaystyle =\pi \i \i \i \i \i \i \i \i \i \i \i \i $=\pi \,r^{2}\,h\,$

Usando le coordinate cilindriche, il volume può essere calcolato mediante integrazione su

= ∫ 0 h ∫ 0 2 π ∫ 0 r s d s d ϕ d z {\displaystyle ={0}^{h}{int _{0}^{2\pi}{int _{0}^{r}s,\s},ds\phi \z} $=\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz$

= π r 2 h {\displaystyle =\pi \i \i \i \i \i \i \i \i \i \i \i \i $=\pi \,r^{2}\,h\,$

Sezione cilindrica

Le sezioni cilindriche sono le intersezioni dei cilindri con i piani. Per un cilindro circolare destro, ci sono quattro possibilità. Un piano tangente al cilindro, incontra il cilindro in una sola linea retta. Spostato parallelamente a se stesso, il piano o non interseca il cilindro o lo interseca in due linee parallele. Tutti gli altri piani intersecano il cilindro in un'ellisse o, quando sono perpendicolari all'asse del cilindro, in un cerchio.

Altri tipi di cilindri

Un cilindro ellittico, o cilindroide, è una superficie quadrica, con la seguente equazione in coordinate cartesiane:

( x a ) 2 + ( y b ) 2 = 1. {\displaystyle \sinistra({frac {x}{a}}destra)^{2}+sinistra({frac {y}{b}}destra)^{2}=1.} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.$

Questa equazione è per un cilindro ellittico, una generalizzazione del cilindro circolare ordinario ( $a = b$ ). Ancora più generale è il cilindro generalizzato: la sezione trasversale può essere qualsiasi curva.

Il cilindro è una quadrica degenere perché almeno una delle coordinate (in questo caso $z$ ) non appare nell'equazione.

Un cilindro obliquo ha le superfici superiore e inferiore spostate l'una dall'altra.

Ci sono altri tipi di cilindri più insoliti. Questi sono i cilindri ellittici immaginari:

( x a ) 2 + ( y b ) 2 = - 1 {\displaystyle \left({frac {x}{a}}destra)^{2}+\left({frac {y}{b}}destra)^{2}=-1} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1$

il cilindro iperbolico:

( x a ) 2 - ( y b ) 2 = 1 {displaystyle \sinistra({frac {x}{a}}destra)^{2}- {frac {y}{b}}destra)^{2}=1} $\left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1$

e il cilindro parabolico:

x 2 + 2 a y = 0. {displaystyle x^{2}+2ay=0,\} $x^{2}+2ay=0.\,$

Geometria proiettiva

In geometria proiettiva, un cilindro è semplicemente un cono il cui vertice è all'infinito.

Questo è utile nella definizione delle coniche degenerate, che richiedono di considerare le coniche cilindriche.

Domande e risposte

D: Che cos'è un cilindro?

R: Un cilindro è una forma geometrica tridimensionale con la superficie formata da punti ad una distanza fissa da un determinato segmento di linea, noto come asse del cilindro. Si può pensare a un prisma circolare e sia la superficie che la forma solida creata all'interno possono essere chiamate cilindro.

D: Da quanto tempo si conoscono l'area superficiale e il volume dei cilindri?

R: L'area superficiale e il volume dei cilindri sono noti fin dall'antichità.

D: Cosa sono i cilindri ellittici, parabolici e iperbolici?

R: I cilindri ellittici, parabolici e iperbolici sono cilindri la cui sezione trasversale è rispettivamente un'ellisse, una parabola o un'iperbole.

D: Come viene definito un cilindro in geometria differenziale?

R: In geometria differenziale, un cilindro è definito in modo più ampio come una superficie governata che è attraversata da una famiglia di rette parallele di un parametro.

D: Cosa significa che qualcosa è "governato"?

R: Essere "governato" significa che ha delle linee rette disegnate su di esso in un modo o nell'altro.

D: Esiste un solo tipo di cilindro?

R: No, esistono molti tipi diversi di cilindri, come i cilindri ellittici, parabolici e iperbolici, che hanno tutti sezioni trasversali diverse.

Autore

AlegsaOnline.com - Cilindro - Leandro Alegsa

Data di creazione: 28 febbraio 2021
Ultimo aggiornamento: 20 aprile 2026

URL: https://it.alegsaonline.com/art/24894