Algoritmo

Algoritmi a confronto

Di solito c'è più di un modo per risolvere un problema. Ci possono essere molte ricette diverse per fare un certo piatto che sembra diverso ma che alla fine ha lo stesso sapore. Lo stesso vale per gli algoritmi. Tuttavia, alcuni di questi modi saranno migliori di altri. Se una ricetta ha bisogno di molti ingredienti complicati che non avete, non è buona come una ricetta semplice. Quando guardiamo agli algoritmi come un modo di risolvere i problemi, spesso vogliamo sapere quanto tempo impiegherebbe un computer a risolvere il problema usando un particolare algoritmo. Quando scriviamo algoritmi, ci piace che il nostro algoritmo impieghi il minor tempo possibile in modo da poter risolvere il nostro problema il più velocemente possibile.

In cucina, alcune ricette sono più difficili da fare di altre, perché richiedono più tempo per finire o hanno più cose da tenere sotto controllo. È lo stesso per gli algoritmi, e gli algoritmi sono migliori quando sono più facili da fare per il computer. La cosa che misura la difficoltà di un algoritmo si chiama complessità. Quando chiediamo quanto è complesso un algoritmo, spesso vogliamo sapere quanto tempo impiegherà un computer per risolvere il problema che vogliamo che risolva.

Ordinamento

Questo è un esempio di un algoritmo per ordinare le carte con i colori in pile dello stesso colore:

1. Raccogli tutte le carte.
2. Prendi una carta dalla tua mano e guarda il colore della carta.
3. Se c'è già un mazzo di carte di quel colore, metti questa carta su quel mazzo.
4. Se non c'è un mazzo di carte di quel colore, fai un nuovo mazzo solo di questo colore.
5. Se c'è ancora una carta in mano, torna al secondo passo.
6. Se non c'è ancora una carta in mano, allora le carte sono ordinate. Hai finito.

Ordinamento per numeri

Questi sono esempi di algoritmi per ordinare una pila di carte con molti numeri diversi, in modo che i numeri siano in ordine.

I giocatori iniziano con una pila di carte che non sono state ordinate.

Primo algoritmo

Questo algoritmo passa attraverso la pila di carte, una carta alla volta. Questa carta viene confrontata con la carta successiva nella pila. Si noti che questa posizione cambia solo nel passo 6. Questo algoritmo è chiamato bubble sort. È lento.

1. Se la pila di carte è vuota, o contiene solo una carta, è ordinata; hai finito.
2. Prendi la pila di carte. Guarda la prima carta (la più in alto) della pila.
3. La carta che stai guardando è la carta A. La posizione in cui si trova attualmente la carta A è nella pila P.
4. Se non ci sono più carte nella pila dopo la carta A, vai al punto 8.
5. La prossima carta nella pila è la carta B.
6. Se la carta B ha un numero più basso della carta A, scambia le posizioni delle carte A e B. Ricordati di averlo fatto. Quando scambi le carte, non cambiare la posizione P.
7. Se c'è un'altra carta nella pila dopo la posizione P, guardala; torna al punto 3.
8. Se non hai cambiato la posizione di nessuna carta nell'ultima corsa, hai finito; la pila di carte è ordinata.
9. Altrimenti tornate al punto 2.

Esempio passo dopo passo

Prendiamo una pila di carte con i numeri "5 1 4 2 8", e ordiniamola dal numero più piccolo al più grande usando questo algoritmo. In ogni passo, l'algoritmo confronta gli elementi scritti in grassetto. La parte superiore della pila di carte è a sinistra.

Primo passaggio:
( 5 1 4 2 8 ) → {\displaystyle \to } ( 1 5 4 2 8 ) Qui l'algoritmo confronta i primi due elementi e li scambia.
( 1 5 4 2 8 ) → {\displaystyle \to } ( 1 4 5 2 8 )
( 1 4 5 2 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 ) Questi elementi sono già in ordine, quindi l'algoritmo non li scambia.
Secondo passaggio:
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Ora, la pila di carte è già ordinata, ma il nostro algoritmo non lo sa. L'algoritmo ha bisogno di un intero passaggio senza alcuno scambio per sapere che è ordinato.
Terzo passaggio:
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to }
( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Infine, l'array è ordinato e l'algoritmo può fermarsi.

Storia

Questo è un algoritmo di facile comprensione per l'ordinamento. Gli scienziati informatici lo hanno chiamato Bubble sort, perché gli elementi più piccoli saliranno in cima, cambiando la loro posizione ad ogni passaggio. Sfortunatamente, l'algoritmo non è molto buono, perché ha bisogno di molto tempo (molti passaggi attraverso la pila di carte) per ordinare.

Secondo algoritmo

Questo algoritmo usa un'altra idea. A volte risolvere un problema è difficile, ma il problema può essere cambiato in modo che sia fatto di problemi più semplici che sono più facili da risolvere. Questo si chiama ricorsione. È più difficile da capire del primo esempio, ma darà un algoritmo migliore.

Idea di base

1. Se la pila non ha carte, o ha solo una carta, è ordinata e hai finito.
2. Dividi la pila di carte in due metà di circa la stessa dimensione. Se c'è un numero dispari di carte, una delle due pile avrà una carta in più dell'altra.
3. Ordina ciascuna delle due pile usando questo algoritmo (per ogni pila, inizia dal punto 1 di questa lista).
4. Unisci le due pile ordinate insieme, come descritto di seguito.
5. Il risultato è una pila di carte ordinata. Avete finito.

Fusione di due pile insieme

Questo funziona con due pile di carte. Una di esse è chiamata A, l'altra è chiamata B. C'è una terza pila che è vuota all'inizio, chiamata C. Alla fine, conterrà il risultato.

1. Se la pila A o la pila B è vuota, metti tutte le carte della pila che non è vuota in cima alla pila C; hai finito, la pila C è il risultato della fusione. (Nota: prendi l'intera pila e mettila sulla pila C; farlo carta per carta cambierà l'ordine e non funzionerà come dovrebbe).
2. Guarda le carte superiori della pila A e della pila B. Metti quella con il numero più basso in cima alla pila C. Se la pila C non aveva carte, ora ne avrà una.
3. Se nella pila A o nella pila B rimangono delle carte, torna al passo 1 per ordinarle.

Storia

John von Neumann ha sviluppato questo algoritmo nel 1945. Non lo chiamò Ordinamento per numeri, ma Mergesort. È un algoritmo molto buono per l'ordinamento, rispetto ad altri.

Terzo algoritmo

Il primo algoritmo impiega molto più tempo per ordinare le carte rispetto al secondo, ma può essere migliorato (reso migliore). Guardando l'ordinamento a bolle, si può notare che le carte con numeri alti si muovono dalla cima della pila abbastanza velocemente, ma le carte con numeri bassi in fondo alla pila impiegano molto tempo per salire (spostarsi in cima). Per migliorare il primo algoritmo ecco l'idea:

Invece di confrontare due carte che sono una accanto all'altra, all'inizio viene scelta una carta "speciale". Tutte le altre carte vengono poi confrontate con questa carta.

1. Iniziamo con una pila A. Ci saranno altre due pile B e C, che verranno create in seguito.
2. Se la pila A non ha carte, o ha solo una carta, abbiamo finito di ordinare.
3. Una carta viene presa dalla pila A, se possibile a caso. Questo è chiamato pivot.
4. Tutte le carte rimanenti della pila A vengono confrontate con questo perno. Le carte con un numero minore vanno nella pila B, quelle con un numero uguale o maggiore vanno nella pila C.
5. Se ci sono delle carte nelle pile B o C, queste pile devono essere ordinate con lo stesso algoritmo (iniziare dalla pos 1 di questa lista sia per la pila B che per la pila C a turno).
6. Fatto. La pila di carte ordinata ha prima la pila ordinata B, poi il pivot, e poi la pila ordinata C.

Storia

Questo algoritmo è stato sviluppato da C. A. R. Hoare nel 1960. È uno degli algoritmi di ordinamento più usati oggi. È chiamato Quicksort.

Animazione che mostra come funziona un ordinamento a bolle


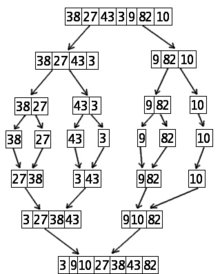
Ordinamento di 7 numeri usando il secondo algoritmo di ordinamento per numeri (Mergesort)


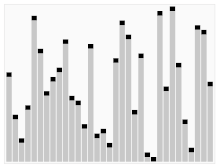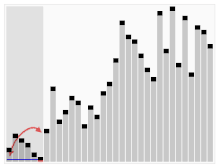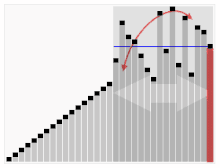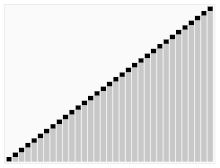
Il terzo algoritmo per ordinare le carte. L'elemento con la barra rossa viene scelto come perno. All'inizio è l'elemento tutto a destra. Questo algoritmo è chiamato Quicksort.

Mettere insieme gli algoritmi

Se i giocatori hanno carte con colori e numeri, possono ordinarle per colore e numero se fanno l'algoritmo "ordinamento per colori", poi fanno l'algoritmo "ordinamento per numeri" per ogni pila colorata, poi mettono insieme le pile.

Gli algoritmi di ordinamento per numeri sono più difficili da fare dell'algoritmo di ordinamento per colori, perché potrebbero dover rifare i passi molte volte. Si potrebbe dire che l'ordinamento per numeri è più complesso.

Pagine correlate

• L'algoritmo euclideo è stato trovato più di 2000 anni fa. È in grado di trovare il massimo comune divisore di due numeri.