Funzione di Heaviside
La funzione di Heaviside, H è una funzione non continua il cui valore è zero per un ingresso negativo e uno per un ingresso positivo.
La funzione è usata nella matematica della teoria del controllo per rappresentare un segnale che si accende in un determinato momento e rimane acceso indefinitamente. Il suo nome deriva dall'inglese Oliver Heaviside.
La funzione di Heaviside è l'integrale della funzione delta di Dirac: H′ = δ. Questo è talvolta scritto come
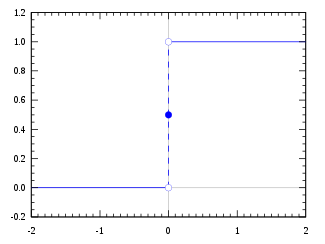
La funzione di passo di Heaviside, usando la convenzione del semimassimo
Forma discreta
Possiamo anche definire una forma alternativa della funzione di passo di Heaviside come funzione di una variabile discreta n:
H [ n ] = { 0 , n < 0 1 , n ≥ 0 {displaystyle H[n]={begin{cases}0,&n<0\1,&n\geq 0\end{cases}}
dove n è un numero intero.
Oppure
H ( x ) = lim z → x - ( | z | / z + 1 ) / 2 ) {\displaystyle H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)}
L'impulso unitario a tempo discreto è la prima differenza del passo a tempo discreto
δ [ n ] = H [ n ] - H [ n - 1 ] . {\displaystyle \delta \left[n\right]=H[n]-H[n-1]. }
Questa funzione è la sommatoria cumulativa del delta di Kronecker:
H [ n ] = ∑ k = - ∞ n δ [ k ] {\displaystyle H[n]=sum _{k=-\infty }^{n}delta [k]\n,}
dove
δ [ k ] = δ k , 0 {displaystyle \delta [k]=\delta _{k,0},}
è la funzione d'impulso unitaria discreta.
Rappresentazioni
Spesso è utile una rappresentazione integrale della funzione di passo di Heaviside:
H ( x ) = lim ϵ → 0 + - 1 2 π i ∫ - ∞ ∞ 1 τ + i ϵ e - i x τ d τ = lim ϵ → 0 + 1 2 π i ∫ - ∞ ∞ 1 τ - i ϵ e i x τ d τ . H(x)=lim _{epsilon \a 0^{+}-{1 \sopra 2\pi \mathrm {i} 1 su \tau +mathrm {i} ‖epsilon ‗mathrm ‗e‖ ^-{mathrm {i} x\tau {mathrm {d} \tau ={lim _{epsilon \a 0^{+}{1 \sopra 2\pi \mathrm {i} 1 su 2pi \mathrm {i}, \mathrm {i}, \mathrm {i}, \mathrm {i}, \mathrm {i}, \mathrm {i}, \mathrm {i}. ‗epsilon ‗mathrm ‗e‖ ^{mathrm {i} x\tau {mathrm {d} \tau . }
H(0)
Il valore della funzione a 0 può essere definito come H(0) = 0, H(0) = ½ o H(0) = 1.
H ( x ) = 1 + sgn ( x ) 2 = { 0 , x < 0 1 2 , x = 0 1 , x > 0. {\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}}
Pagine correlate
- Trasformata di Laplace
Domande e risposte
D: Che cos'è la funzione di Heaviside?
R: La funzione di Heaviside è una funzione non continua il cui valore è zero per un ingresso negativo e uno per un ingresso positivo.
D: Perché la funzione Heaviside è utilizzata nella teoria del controllo?
R: La funzione Heaviside viene utilizzata nella teoria del controllo per rappresentare un segnale che si accende in un momento specifico e rimane acceso indefinitamente.
D: Chi è la persona che ha dato il nome alla funzione di Heaviside?
R: La funzione Heaviside prende il nome dall'inglese Oliver Heaviside.
D: Qual è la relazione tra la funzione di Heaviside e la funzione delta di Dirac?
R: La funzione Heaviside è l'integrale della funzione delta di Dirac: H′(x)= δ(x).
D: Che cosa produce la funzione di Heaviside per ingressi positivi?
R: La funzione di Heaviside dà come risultato uno per gli ingressi positivi.
D: Che cosa produce la funzione di Heaviside per gli ingressi negativi?
R: La funzione Heaviside produce zero per gli ingressi negativi.
D: Che tipo di funzione è la funzione di Heaviside?
R: La funzione Heaviside è una funzione non continua.
Cerca nell'enciclopedia
![{\displaystyle H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}}](https://www.alegsaonline.com/image/efb65c686bdec46712eae1997c363f7ef8709b79.svg)

![{\displaystyle \delta \left[n\right]=H[n]-H[n-1].}](https://www.alegsaonline.com/image/e6c417f161a7987a4db18818743eeb23494b0feb.svg)
![{\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,}](https://www.alegsaonline.com/image/5db28db3163e2940aaf93d0fc180edb19d865d32.svg)
![{\displaystyle \delta [k]=\delta _{k,0}\,}](https://www.alegsaonline.com/image/97a99ab7d257c74f38fbb2d42c8e42e1cb16d0e9.svg)

