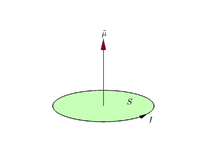
Momento magnetico

Il momento magnetico di un magnete è una quantità che determina la forza che il magnete può esercitare sulle correnti elettriche e la coppia che un campo magnetico eserciterà su di esso. Un circuito di corrente elettrica, un magnete a barra, un elettrone, una molecola e un pianeta hanno tutti momenti magnetici.

Sia il momento magnetico che il campo magnetico possono essere considerati come vettori che hanno una grandezza e una direzione. La direzione del momento magnetico punta dal polo sud al polo nord di un magnete. Anche il campo magnetico prodotto da un magnete è proporzionale al suo momento magnetico. Più precisamente, il termine momento magnetico si riferisce normalmente al momento di dipolo magnetico di un sistema, che produce il primo termine nell'espansione multipolare di un campo magnetico generale. La componente di dipolo del campo magnetico di un oggetto è simmetrica rispetto alla direzione del suo momento di dipolo magnetico, e diminuisce come l'inverso del cubo della distanza dall'oggetto.

Due definizioni di momento

Nei libri di testo, vengono utilizzati due approcci complementari per definire i momenti magnetici. Nei libri di testo precedenti al 1930, erano definiti usando i poli magnetici. I libri di testo più recenti li definiscono in termini di correnti di Ampèrian.

Definizione di polo magnetico

I fisici rappresentano le fonti di momenti magnetici nei materiali come poli. I poli nord e sud sono un'analogia con le cariche positive e negative in elettrostatica. Consideriamo un magnete a barra che ha poli magnetici di uguale grandezza ma di polarità opposta. Ogni polo è la fonte della forza magnetica che si indebolisce con la distanza. Poiché i poli magnetici sono sempre in coppia, le loro forze si annullano parzialmente perché mentre un polo tira, l'altro respinge. Questa cancellazione è maggiore quando i poli sono vicini l'uno all'altro, cioè quando il magnete a barra è corto. La forza magnetica prodotta da un magnete a barra, in un dato punto dello spazio, dipende quindi da due fattori: sia dalla forza p {displaystyle p} $p$ dei suoi poli, sia dal vettore l {displaystyle \mathbf {l} che $\mathbf {l}$ li separa. Il momento è definito come

m = p l . {\displaystyle \mathbf {m} =p\mathbf {l} . } $\mathbf {m} =p\mathbf {l} .$

Punta nella direzione dal polo sud al polo nord. L'analogia con i dipoli elettrici non dovrebbe essere presa troppo alla larga perché i dipoli magnetici sono associati al momento angolare (vedi Momento magnetico e momento angolare). Tuttavia, i poli magnetici sono molto utili per i calcoli magnetostatici, in particolare nelle applicazioni ai ferromagneti. Chi usa l'approccio dei poli magnetici generalmente rappresenta il campo magnetico con il campo irrotazionale H {displaystyle \mathbf {H} } $\mathbf {H}$ , in analogia con il campo elettrico E {displaystyle \mathbf {E} } $\mathbf {E}$ .

Definizione del ciclo di corrente

Supponiamo che un anello chiuso planare trasporti una corrente elettrica I e abbia un'area vettoriale S. } $\mathbf {S}$ ( x {displaystyle x} , y {displaystyle y} e le $z$ coordinate z di questo vettore sono le aree delle proiezioni dell'anello sulle coordinate y z $yz$ , z x {displaystyle zx} $zx$ e sui $xy$ piani x y {displaystyle xy}). Il suo momento magnetico m {displaystyle \mathbf {m} } $\mathbf {m}$ , vettore, è definito come:

m = I S . {\displaystyle \mathbf {m} =I\mathbf {S} . } $\mathbf {m} =I\mathbf {S} .$

Per convenzione, la direzione dell'area vettoriale è data dalla regola della presa della mano destra (arricciare le dita della mano destra nella direzione della corrente intorno all'anello, quando il palmo della mano "tocca" il bordo esterno dell'anello, e il pollice diritto indica la direzione dell'area vettoriale e quindi del momento magnetico).

Se il ciclo non è planare, il momento è dato come

m = I 2 ∫ r × d r . \mathbf {m} ={frac {I}{2}}int \mathbf {r} \Tempi {rm {d} {mathbf {mathbf {r} . } $\mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} .$

Nel caso più generale di una distribuzione arbitraria di corrente nello spazio, il momento magnetico di tale distribuzione può essere trovato dalla seguente equazione:

m = 1 2 ∫ r × J d V , {displaystyle \mathbf {m} ={frac {1}{2}}int \mathbf {r} \tempi \mathbf {J} V,{rm {d}V,} $\mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}V,$

dove r {displaystyle \mathbf {r} $\mathbf {r}$ è il vettore posizione che punta dall'origine alla posizione dell'elemento di volume, e J è il vettore densità di corrente in quel punto. è il $\mathbf {J}$ vettore della densità di corrente in quel punto.

L'equazione di cui sopra può essere usata per calcolare un momento magnetico di qualsiasi insieme di cariche in movimento, come un solido carico che gira, sostituendo

J = ρ v , {displaystyle \mathbf {J} =\rho \mathbf {v} ,} $\mathbf {J} =\rho \mathbf {v} ,$

dove ρ {displaystyle \rho } $\rho$ è la densità di carica elettrica in un dato punto e v {displaystyle \mathbf {v} $\mathbf {v}$ è la velocità lineare istantanea di quel punto.

Per esempio, il momento magnetico prodotto da una carica elettrica che si muove lungo un percorso circolare è

m = 1 2 q r × v {displaystyle \mathbf {m} ={frac {1}{2}}},q\,\mathbf {r} \tempi \mathbf {v} } $\mathbf {m} ={\frac {1}{2}}\,q\,\mathbf {r} \times \mathbf {v}$ ,

dove r {displaystyle \mathbf {r} $\mathbf {r}$ è la posizione della carica q rispetto al centro del cerchio e v $\mathbf {v}$ è la velocità istantanea della carica.

I praticanti che usano il modello a loop di corrente generalmente rappresentano il campo magnetico con il campo solenoidale B {displaystyle \mathbf {B} } $\mathbf {B}$ , analogo al campo elettrostatico D {displaystyle \mathbf {D} } $\mathbf {D}$ .

Momento magnetico di un solenoide

Una generalizzazione dell'anello di corrente di cui sopra è una bobina multigiro, o solenoide. Il suo momento è la somma vettoriale dei momenti delle singole spire. Se il solenoide ha N {displaystyle N} $N$ spire identiche (avvolgimento monostrato),

m = N I S . {\displaystyle \mathbf {m} =NI\mathbf {S} . } $\mathbf {m} =NI\mathbf {S} .$

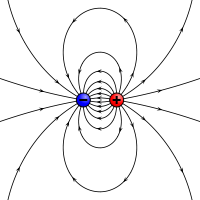
Un analogo elettrostatico di un momento magnetico: due cariche opposte separate da una distanza finita.

Momento m {displaystyle \mathbf {m} $\mathbf {m}$ di un anello di corrente planare con area S {displaystyle S} $S$ e corrente I {displaystyle I} .

Immagine 3-D di un solenoide.

Unità

L'unità del momento magnetico non è un'unità di base nel Sistema Internazionale di Unità (SI) e può essere rappresentata in più di un modo. Per esempio, nella definizione dell'anello di corrente, l'area è misurata in metri quadrati e I {displaystyle I} è misurata in ampere, quindi il momento magnetico è misurato in ampere metri quadrati ( A m 2 {displaystyle {testo{A m}^{2}} ${\text{A m}}^{2}$ ). Nell'equazione per la coppia su un momento, la coppia è misurata in Newton.metri e il campo magnetico in tesla, quindi il momento è misurato in N.m per Tesla ( N.m T - 1 { {displaystyle{N.m T}^{-1}} ${\text{N.m T}}^{-1}$ ). Queste due rappresentazioni sono equivalenti:

A m 2 = N.m T - 1 . A m 2 = N.m T - 1. } $\,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}.$

Nel sistema CGS, ci sono diversi set di unità di elettromagnetismo, di cui i principali sono ESU, Gaussian e EMU. Tra queste, ci sono due unità alternative (non equivalenti) di momento di dipolo magnetico in CGS:

(ESU CGS) 1 statA-cm² = 3,33564095×10-14 (^m2-A o N.m/T)

e (usato più frequentemente)

(EMU CGS e Gaussian-CGS) 1 erg/G = 1 abA-cm² = 10-3 (^m2-A o N.m/T).

Il rapporto di queste due unità CGS non equivalenti (EMU/ESU) è uguale esattamente alla velocità della luce nello spazio libero, espressa in cm/s.

Tutte le formule in questo articolo sono corrette in unità SI, ma in altri sistemi di unità, le formule potrebbero dover essere cambiate. Per esempio, in unità SI, un anello di corrente con corrente I e area A ha momento magnetico I×A (vedi sotto), ma in unità gaussiane il momento magnetico è I×A/c.

Momenti magnetici intrinseci e spin di alcune particelle elementari
Particella	Momento di dipolo magnetico in unità SI (10-27 J/T)	Numero quantico di spin (adimensionale)
elettrone	-9284.764	1/2
protone	14.106067	1/2
neutrone	-9.66236	1/2
muone	-44.904478	1/2
deuterone	4.3307346	1
tritone	15.046094	1/2

Per la relazione tra le nozioni di momento magnetico e magnetizzazione vedi magnetizzazione.

Domande e risposte

D: Qual è il momento magnetico di un magnete?

R: Il momento magnetico di un magnete è una quantità che determina la forza che il magnete può esercitare sulle correnti elettriche e la coppia che un campo magnetico eserciterà su di esso.

D: Quali oggetti hanno un momento magnetico?

R: Una spira di corrente elettrica, un magnete a barra, un elettrone, una molecola e un pianeta hanno tutti un momento magnetico.

D: Come si possono considerare sia il momento magnetico che il campo magnetico?

R: Sia il momento magnetico che il campo magnetico possono essere considerati come vettori aventi una grandezza e una direzione.

D: In quale direzione punta il momento magnetico in un magnete?

R: La direzione del momento magnetico punta dal polo sud al polo nord di un magnete.

D: Qual è la relazione tra il momento magnetico e il campo magnetico di un magnete?

R: Il campo magnetico prodotto da un magnete è proporzionale al suo momento magnetico.

D: A cosa si riferisce normalmente il termine momento magnetico?

R: Più precisamente, il termine momento magnetico si riferisce normalmente al momento di dipolo magnetico di un sistema, che produce il primo termine nell'espansione multipolare di un campo magnetico generale.

D: Come si comporta la componente di dipolo del campo magnetico di un oggetto all'aumentare della distanza dall'oggetto?

R: La componente di dipolo del campo magnetico di un oggetto è simmetrica rispetto alla direzione del suo momento di dipolo magnetico e diminuisce con l'inverso del cubo della distanza dall'oggetto.