Vettore
Un vettore è un oggetto matematico che ha una dimensione, chiamata magnitudine, e una direzione.
Per esempio, un vettore verrebbe usato per mostrare la distanza e la direzione in cui qualcosa si è mosso. Se chiedi indicazioni, e una persona dice "Cammina un chilometro verso il nord", questo è un vettore. Se dice "Cammina un chilometro", senza mostrare una direzione, sarebbe uno scalare.
Di solito disegniamo i vettori come frecce. La lunghezza della freccia è proporzionale alla grandezza del vettore. La direzione in cui punta la freccia è la direzione del vettore.
Esempi di vettori
Esempi di scalari
- La distanza tra due luoghi è di 10 chilometri. Questa distanza non è un vettore perché non contiene una direzione.
- Il numero di frutti in una scatola non è un vettore.
- Una persona che indica non è un vettore perché c'è solo una direzione. Non c'è una grandezza (la distanza dal dito della persona a un edificio, per esempio).
- La lunghezza di un oggetto.
- Un'auto viaggia a 100 chilometri all'ora. Questo non descrive un vettore, poiché c'è solo una grandezza, ma nessuna direzione.
Altri esempi di vettori
- Lo spostamento è un vettore. Lo spostamento è la distanza che qualcosa si sposta in una certa direzione. Una misura della sola distanza è uno scalare.
- La forza che include la direzione è un vettore.
- La velocità è un vettore, perché è una velocità in una certa direzione.
- L'accelerazione è il tasso di cambiamento della velocità. Un oggetto sta accelerando se sta cambiando velocità o direzione.
Come aggiungere vettori
Aggiungere vettori su carta usando il metodo testa-coda
Il metodo Head to Tail dell'addizione di vettori è utile per fare una stima su carta del risultato dell'addizione di due vettori. Per farlo:
- Ogni vettore è disegnato come una freccia con una quantità di lunghezza dietro di essa, dove ogni unità di lunghezza sulla carta rappresenta una certa grandezza del vettore.
- Disegna il prossimo vettore, con la coda del secondo vettore alla testa del primo vettore.
- Ripetere per tutti gli altri vettori: Disegna la coda del prossimo vettore a capo del precedente.
- Tracciate una linea dalla coda del primo vettore alla testa dell'ultimo vettore - questa è la risultante di tutti i vettori.
Si chiama il metodo "Head to Tail", perché ogni testa del vettore precedente porta alla coda del successivo.
Usare il modulo dei componenti
[deve essere spiegato]
Usare la forma componente per aggiungere due vettori significa letteralmente aggiungere le componenti dei vettori per creare un nuovo vettore. Per esempio, lasciamo che a e b siano due vettori bidimensionali. Questi vettori possono essere scritti in termini delle loro componenti.
a = ( a x , a y ) {displaystyle \mathbf {a} =(a_{x},a_{y})} 
b = ( b x , b y ) {displaystyle \mathbf {b} =(b_{x},b_{y})} 
Supponiamo che c sia la somma di questi due vettori, in modo che c = a + b. Ciò significa che c = ( a x + b x , a y + b y ) {\displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} 
.
Ecco un esempio di addizione di due vettori, usando le loro forme componenti.
a = ( 3 , - 1 ) {\displaystyle \mathbf {a} =(3,-1)} 
b = ( 2 , 2 ) {\displaystyle \mathbf {b} =(2,2)} 
c = a + b {\displaystyle \mathbf {c} =\mathbf {a} +mathbf {b} } 
= ( a x + b x , a y + b y ) {\displaystyle =(a_{x}+b_{x},a_{y}+b_{y})} 
= ( 3 + 2 , - 1 + 2 ) {\displaystyle =(3+2,-1+2)} 
= ( 5 , 1 ) {\displaystyle =(5,1)} 
Questo metodo funziona per tutti i vettori, non solo per quelli bidimensionali.
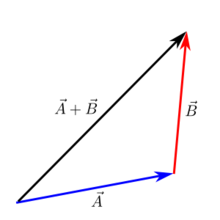
Aggiunta testa-coda
Come moltiplicare i vettori
Usando il prodotto del punto
Il prodotto di punti è un metodo per moltiplicare i vettori. Produce uno scalare. Utilizza la forma componente:
a = ( 2 , 3 ) b = ( 1 , 4 ) a ⋅ b = ( 2 , 3 ) ⋅ ( 1 , 4 ) = ( 2 ⋅ 1 ) + ( 3 ⋅ 4 ) = 2 + 12 = 14 {\displaystyle {\begin{aligned}\mathbf {a} =(2,3)\mathbf {b} =(1,4)\mathbf {a} \cdot \mathbf {b} =(2,3)\cdot (1,4)\mathbf =(2\cdot 1)+(3\cdot 4)\mathbf=2+12=14\end{aligned}} 
Usando il prodotto incrociato
Il prodotto incrociato è un altro metodo per moltiplicare i vettori. Produce un altro vettore. Usando la forma componente:
a × b = | a | b | sin ( θ ) n {\displaystyle \mathbf {a} \times \mathbf {b} =|mathbf {a} \sin(\theta )\mathbf {mathbf {n} } 
Qui | a | {displaystyle |mathbf {a} 
si intende la lunghezza di a {displaystyle \mathbf {a} 
e n {displaystyle \mathbf {n} 
è il vettore unitario perpendicolare sia ad a {displaystyle \mathbf {a} e b {displaystyle \mathbf {b} } 
.
Moltiplicando per uno scalare
Per moltiplicare un vettore per uno scalare (un numero normale), si moltiplica il numero per ogni componente del vettore:
c x = ( c x 1 , c x 2 , . . . , c x n ) {\displaystyle c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})} 
Un esempio di questo è
c = 5 x = ( 3 , 4 ) c x = ( 5 ⋅ 3 , 5 ⋅ 4 ) = ( 15 , 20 ) {\displaystyle {\begin{aligned}c=5\mathbf {x} =(3,4)\c\,\mathbf {x} =(5\cdot 3,5\cdot 4)\\\\(15,20)\end{aligned}} 
Pagine correlate
- Grafica vettoriale
- Campo vettoriale
Domande e risposte
D: Che cos'è un vettore?
R: Un vettore è un oggetto matematico che ha una dimensione, chiamata magnitudine, e una direzione. Spesso è rappresentato da lettere in grassetto o come un segmento di linea da un punto ad un altro.
D: Come si disegnano di solito i vettori?
R: Di solito disegniamo i vettori come frecce. La lunghezza della freccia è proporzionale alla grandezza del vettore e la direzione verso cui punta la freccia è la direzione del vettore.
D: Cosa significa quando qualcuno chiede indicazioni?
R: Quando si chiedono indicazioni stradali, se si dice "Cammina un chilometro verso Nord", si tratta di un vettore, ma se si dice "Cammina un chilometro", senza indicare una direzione, si tratta di uno scalare.
D: Quali sono alcuni esempi di utilizzo dei vettori?
R: I vettori possono essere utilizzati per mostrare la distanza e la direzione in cui qualcosa si è mosso. Possono anche essere utilizzati quando si chiedono indicazioni o si naviga in un'area.
D: Come vengono rappresentati matematicamente i vettori?
R: I vettori sono spesso rappresentati da lettere in grassetto (come u, v, w) o come un segmento di linea da un punto a un altro (come A→B).
D: Cosa significa quando qualcosa viene definito scalare?
R: Quando qualcosa viene definito scalare, significa che non è associata ad alcuna informazione direzionale, ma solo a valori numerici come la distanza o la velocità.
