Sezione aurea
Con un numero a e un altro numero più piccolo b, il rapporto tra i due numeri si trova dividendoli. Il loro rapporto è a/b. Un altro rapporto si trova sommando i due numeri insieme a+b e dividendo questo per il numero più grande a. Il nuovo rapporto è (a+b)/a. Se questi due rapporti sono uguali allo stesso numero, allora quel numero è chiamato rapporto aureo. La lettera greca φ \varphi \varphi \varphi \varphi \varphi \varphi \varphi \varphi \varphi 
(phi) è di solito usato come nome per il rapporto aureo.
Ad esempio, se b = 1 e a/b = φ {\fscx130\fscy130\frx40}- Se b = 1 e a/b = φ {\fscx130\fscy130\frx40}... poi un = φ {\fscx130\fscy130\frx40}. . Il secondo rapporto (a+b)/a è quindi ( φ + 1 ) / φ {\i\i}. 
. Perché questi due rapporti sono uguali, questo è vero:
φ = φ + 1 φ {\fscx130\fscy130\frx40}Varphi ={\frac {\fscx130\fscy130\frx40}Varphi +1{\fscy130\frx40}}Varphi.
Un modo per scrivere questo numero è
φ = 1 + 5 2 2 {\a6}{\a6}}varphi ={\a6}frac {1+{\a6}}}{2}}
5 {\displaystyle {\sqrt {5}}}} 
è come qualsiasi numero che, se moltiplicato per se stesso, fa 5 (o quale numero è moltiplicato): 5 × 5 = 5 {\displaystyle {\sqrt {5}}} {\sqrt {5}}=5}
.
Il rapporto aureo è un numero irrazionale. Se una persona cerca di scriverlo, non si fermerà mai e non farà mai uno schema, ma inizierà in questo modo: 1,6180339887... Una cosa importante di questo numero è che una persona può sottrarre 1 da esso o dividere 1 per esso. In entrambi i casi, il numero continuerà ad andare avanti e non si fermerà mai.
Rettangolo dorato
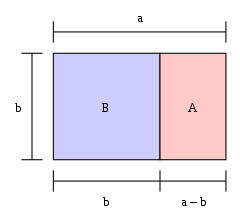
Se la lunghezza di un rettangolo divisa per la sua larghezza è uguale al rapporto aureo, allora il rettangolo è un "rettangolo dorato". Se un quadrato è tagliato da un'estremità di un rettangolo dorato, allora l'altra estremità è un nuovo rettangolo dorato. Nell'immagine, il grande rettangolo (blu e rosa insieme) è un rettangolo dorato perché a / b = φ {\fscx130\fscy130\frx40} a/b = φ {\fscx130\fscy130\frx40}varphi }. 
. La parte blu (B) è un quadrato. La parte rosa di per sé (A) è un altro rettangolo dorato perché b / ( a - b ) = φ {\fscx130\fscy130\frx40} φ {\fscx130\fscy130\frx40} \fscy130\frx40}. 
. Il rettangolo grande e il rettangolo rosa hanno la stessa forma, ma il rettangolo rosa è più piccolo e viene girato.
Il grande rettangolo BA è un rettangolo dorato; cioè la proporzione b:a è 1: φ φ \varphi \varphi \varphi \varphi \varphi \varphi . Per un tale rettangolo, e solo per i rettangoli di quella specifica proporzione, se togliamo il quadrato B, ciò che rimane, A, è un altro rettangolo dorato; cioè con le stesse proporzioni del rettangolo originale.
Numeri di Fibonacci
I numeri di Fibonacci sono una lista di numeri. Una persona può trovare il numero successivo nella lista aggiungendo gli ultimi due numeri insieme. Se una persona divide un numero della lista per il numero che l'ha preceduto, questo rapporto si avvicina sempre più al rapporto aureo.
| Numero di Fibonacci | diviso per quello prima | rapporto |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ φ in stile varphi φ | = 1.6180... |
Il rapporto aureo in natura
In natura, il rapporto aureo è spesso utilizzato per la disposizione delle foglie o dei fiori. Questi utilizzano l'angolo dorato di circa 137,5 gradi. Foglie o fiori disposti in tale angolo meglio utilizzare la luce del sole.
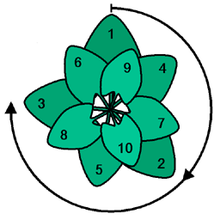
L'utilizzo dell'angolo dorato sfrutterà in modo ottimale la luce del sole. Questa è una vista dall'alto.
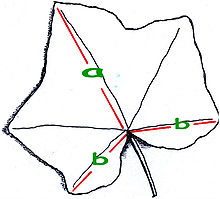
Una foglia di edera comune, che mostra il rapporto aureo
Domande e risposte
D: Qual è il rapporto tra due numeri?
R: Il rapporto tra due numeri si trova dividendoli, quindi il rapporto sarebbe a/b.
D: Come si può trovare un altro rapporto?
R: Si può trovare un altro rapporto sommando i due numeri e poi dividendo questa somma per il numero più grande, a. Questo nuovo rapporto sarebbe (a+b)/a.
D: Come si chiama quando questi due rapporti sono uguali tra loro?
R: Quando questi due rapporti sono uguali tra loro, si chiama rapporto aureo. Di solito viene rappresentato con la lettera greca צ o phi.
D: Se b = 1 e a/b = צ , cosa significa per a?
R: Se b = 1 e a/b = צ , significa che anche a = צ.
D: Come si può scrivere questo numero?
R: Un modo per scrivere questo numero è צ = 1 + 5 / 2 = 1,618...
D: Cosa significa sottrarre 1 da questo numero o dividere 1 per esso?
R: Se sottrae 1 da esso o divide 1 per esso, otterrà lo stesso numero - in altre parole, entrambi saranno uguali al rapporto aureo.
D: Il rapporto aureo è un numero irrazionale?
R: Sì, il rapporto aureo è un numero irrazionale, il che significa che se qualcuno cerca di scriverlo, non ci sarà mai una fine né uno schema, ma solo un inizio come "1,6180339887...".
