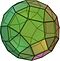
Solido archimedeo
In geometria, un solido archimedeo è una forma convessa composta da poligoni. È un poliedro con le seguenti proprietà:
- Ogni faccia è costituita da un poligono regolare
- Tutti gli angoli della forma sembrano uguali
- La forma non è né un solido platonico, né un prisma, né un antiprisma.
A seconda di come si contano, ci sono tredici o quindici forme di questo tipo. Di due di queste forme, ci sono due versioni che non possono essere rese congruenti usando la rotazione. I solidi archimedei prendono il nome dal matematico greco Archimede, che probabilmente li scoprì nel III secolo a.C. Gli scritti di Archimede sono andati perduti, ma Pappo di Alessandria li riassunse nel IV secolo. Durante il Rinascimento, artisti e matematici apprezzarono le forme pure e riscoprirono tutte queste forme. Johannes Kepler probabilmente completò questa ricerca intorno al 1620.
La costruzione di un solido archimedeo richiede almeno due poligoni diversi.
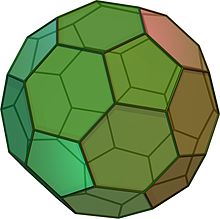
Un icosaedro troncato assomiglia a un pallone da calcio. È composto da 12 pentagoni equilateri e 20 esagoni regolari. Ha 60 vertici e 90 spigoli. È un solido archimedeo
Proprietà
- I solidi archimedei sono fatti di poligoni regolari, quindi tutti gli spigoli hanno la stessa lunghezza.
- Tutti i solidi archimedei possono essere prodotti dai solidi platonici, "tagliando i bordi" del solido platonico.
- Il tipo di poligoni che si incontrano in un angolo ("vertice") caratterizza sia il solido archimedeo che quello platonico
Relazione con i solidi platonici
I solidi platonici possono essere trasformati in solidi archimedei seguendo una serie di regole per la loro costruzione.
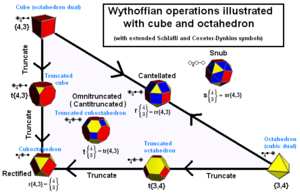
I solidi archimedei possono essere costruiti come posizioni generatrici in un caleidoscopio
Elenco di solidi archimedei
Il seguente è un elenco di tutti i solidi archimedei
| Immagine | Nome | Volti | Tipo | Bordi | Vertici |
|
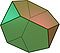
| Tetraedro troncato | 8 | 4 triangoli 4 esagoni | 18 | 12 |
|
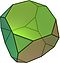
| 14 | 8 triangoli 6 piazze | 24 | 12 | |
|
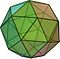
| Cubo troncato | 14 | 8 triangoli 6 ottagoni | 36 | 24 |
|
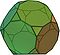
| Ottaedro troncato | 14 | 6 piazze 8 esagoni | 36 | 24 |
|
| Rombicubottaedro | 26 | 8 triangoli 18 piazze | 48 | 24 |
|
| Cubottaedro troncato | 26 | 12 piazze 8 esagoni 6 ottagoni | 72 | 48 |
|
| Cubo snub (2 versioni a specchio) | 38 | 32 triangoli 6 piazze | 60 | 24 |
|
| Icosidodecaedro | 32 | 20 triangoli 12 pentagoni | 60 | 30 |
|
| Dodecaedro troncato | 32 | 20 triangoli 12 decagoni | 90 | 60 |
|
| Icosaedro troncato | 32 | 12 pentagoni 20 esagoni | 90 | 60 |
|
| Rombicosidodecaedro | 62 | 20 triangoli30 quadrati12 | 120 | 60 |
|
| Icosidodecaedro troncato | 62 | 30 piazze 20 esagoni 12 decagoni | 180 | 120 |
|
| Snub dodecaedro (2 versioni speculari) | 92 | 80 triangoli 12 pentagoni | 150 | 60 |
Domande e risposte
D: Che cos'è un solido archimedeo?
R: Un solido archimedeo è una forma convessa composta da poligoni che ha le proprietà di ogni faccia di essere un poligono regolare, di avere tutti gli angoli uguali e di non essere un solido platonico, un prisma o un antiprisma.
D: Quanti solidi archimedei esistono?
R: A seconda di come vengono contati, ci sono tredici o quindici solidi archimedei.
D: Chi ha scoperto i solidi archimedei?
R: I solidi archimedei prendono il nome dal matematico greco antico Archimede, che probabilmente li scoprì nel III secolo a.C..
D: Cosa fece Pappo di Alessandria con gli scritti di Archimede?
R: Pappo di Alessandria riassunse gli scritti di Archimede sui solidi archimedei nel IV secolo.
D: Perché artisti e matematici riscoprirono i solidi archimedei durante il Rinascimento?
R: Durante il Rinascimento, gli artisti e i matematici apprezzavano le forme pure e i solidi archimedei erano considerati forme pure.
D: Quando Johannes Kepler completò la ricerca di tutti i solidi archimedei?
R: Johannes Kepler probabilmente completò la ricerca di tutti i solidi archimedei intorno al 1620.
D: Cosa è necessario per costruire un solido archimedeo?
R: La costruzione di un solido archimedeo richiede almeno due poligoni diversi.
Cerca nell'enciclopedia