Deviazione standard
La deviazione standard è un numero usato per dire come le misurazioni per un gruppo sono sparse dalla media (media), o dal valore atteso. Una bassa deviazione standard significa che la maggior parte dei numeri sono vicini alla media. Una deviazione standard alta significa che i numeri sono più sparsi.
Il margine di errore riportato è di solito il doppio della deviazione standard. Gli scienziati riportano comunemente la deviazione standard dei numeri dal numero medio negli esperimenti. Spesso decidono che solo le differenze più grandi di due o tre volte la deviazione standard sono importanti. La deviazione standard è utile anche nel denaro, dove la deviazione standard dell'interesse guadagnato mostra quanto diverso possa essere l'interesse guadagnato da una persona dalla media.
Molte volte, solo un campione, o una parte di un gruppo può essere misurato. Allora un numero vicino alla deviazione standard per l'intero gruppo può essere trovato con un'equazione leggermente diversa chiamata deviazione standard del campione, spiegata di seguito.
.png)
Un grafico di una distribuzione normale (o curva a campana). Ogni banda colorata ha una larghezza di una deviazione standard.
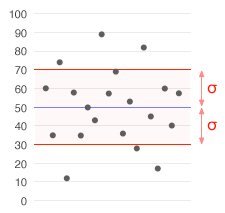
Una serie di dati con una media di 50 (mostrata in blu) e una deviazione standard (σ) di 20.
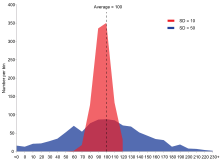
Esempio di due popolazioni campione con la stessa media e diverse deviazioni standard. La popolazione rossa ha media 100 e deviazione standard 10; la popolazione blu ha media 100 e deviazione standard 50.
Esempio di base
Consideriamo un gruppo con i seguenti otto numeri:
2 , 4 , 4 , 4 , 5 , 5 , 7 , 9 {displaystyle 2,\ 4,\ 4,\ 4,\ 5,\ 5,\ 7,\ 9}
Questi otto numeri hanno una media di 5:
2 + 4 + 4 + 4 + 4 + 5 + 5 + 7 + 9 8 = 5 {displaystyle {\frac {2+4+4+4+5+5+7+9}{8}=5}
Per calcolare la deviazione standard della popolazione, trova prima la differenza di ogni numero della lista dalla media. Poi eleva al quadrato il risultato di ogni differenza:
( 2 - 5 ) 2 = ( - 3 ) 2 = 9 ( 5 - 5 ) 2 = 0 2 = 0 ( 4 - 5 ) 2 = ( - 1 ) 2 = 1 ( 5 - 5 ) 2 = 0 2 = 0 ( 4 - 5 ) 2 = ( - 1 ) 2 = 1 ( 7 - 5 ) 2 = 2 2 = 4 ( 4 - 5 ) 2 = ( - 1 ) 2 = 1 ( 9 - 5 ) 2 = 4 2 = 16 {\displaystyle {\begin{array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}}
Poi, trova la media di questi valori (somma divisa per il numero di numeri). Per ultimo, prendi la radice quadrata:
( 9 + 1 + 1 + 1 + 1 + 0 + 0 + 4 + 16 ) 8 = 2 {displaystyle {\sqrt {\frac {(9+1+1+1+0+0+4+16)}{8}}=2}
La risposta è la deviazione standard della popolazione. La formula è vera solo se gli otto numeri con cui abbiamo iniziato sono l'intero gruppo. Se sono solo una parte del gruppo scelto a caso, allora dovremmo usare 7 (che è n - 1) invece di 8 (che è n) nella parte inferiore (denominatore) del penultimo passo. Allora la risposta è la deviazione standard del campione. Questa è chiamata correzione di Bessel.
Altri esempi
Un esempio di vita reale leggermente più difficile: L'altezza media degli uomini adulti negli Stati Uniti è di 70", con una deviazione standard di 3". Una deviazione standard di 3" significa che la maggior parte degli uomini (circa il 68%, assumendo una distribuzione normale) hanno un'altezza da 3" più alta a 3" più corta della media (67"-73") - una deviazione standard. Quasi tutti gli uomini (circa il 95%) hanno un'altezza da 6" più alta a 6" più corta della media (64"-76") - due deviazioni standard. Tre deviazioni standard includono tutti i numeri per il 99,7% della popolazione campione studiata. Questo è vero se la distribuzione è normale (a forma di campana).
Se la deviazione standard fosse zero, allora tutti gli uomini sarebbero esattamente alti 70". Se la deviazione standard fosse di 20", allora alcuni uomini sarebbero molto più alti o molto più bassi della media, con una gamma tipica di circa 50"-90".
Per un altro esempio, ognuno dei tre gruppi {0, 0, 14, 14}, {0, 6, 8, 14} e {6, 6, 8, 8} ha una media di 7. Ma le loro deviazioni standard sono 7, 5 e 1. Il terzo gruppo ha una deviazione standard molto più piccola degli altri due perché i suoi numeri sono tutti vicini a 7. L'idea di base è che la deviazione standard ci dice quanto lontano dalla media tende ad essere il resto dei numeri. Avrà le stesse unità dei numeri stessi. Se, per esempio, il gruppo {0, 6, 8, 14} è l'età di un gruppo di quattro fratelli in anni, la media è 7 anni e la deviazione standard è 5 anni.
La deviazione standard può servire come misura dell'incertezza. Nella scienza, per esempio, la deviazione standard di un gruppo di misure ripetute aiuta gli scienziati a sapere quanto sono sicuri del numero medio. Quando si decide se le misure di un esperimento concordano con una previsione, la deviazione standard di queste misure è molto importante. Se il numero medio degli esperimenti è troppo lontano dal numero previsto (con la distanza misurata in deviazioni standard), allora la teoria testata potrebbe non essere giusta. Vedi intervallo di predizione.
Esempi di applicazione
L'utilità di capire la deviazione standard di un insieme di valori sta nel sapere quanto è grande la differenza dalla "media" (media).
Meteo
Come semplice esempio, si consideri la media delle alte temperature giornaliere per due città, una nell'entroterra e una vicino all'oceano. È utile capire che la gamma di temperature massime giornaliere per le città vicine all'oceano è più piccola di quella delle città dell'entroterra. Queste due città possono avere la stessa temperatura media giornaliera. Tuttavia, la deviazione standard dell'alta temperatura giornaliera per la città costiera sarà inferiore a quella della città interna.
Sport
Un altro modo di vedere la cosa è considerare le squadre sportive. In qualsiasi sport, ci saranno squadre che sono brave in alcune cose e non in altre. Le squadre che sono classificate più in alto non mostreranno molte differenze di abilità. Fanno bene nella maggior parte delle categorie. Più bassa è la deviazione standard della loro abilità in ogni categoria, più sono equilibrate e coerenti. Le squadre con una deviazione standard più alta, tuttavia, saranno meno prevedibili. Una squadra che di solito è cattiva nella maggior parte delle categorie avrà una deviazione standard bassa. Una squadra che di solito è buona nella maggior parte delle categorie avrà anche una bassa deviazione standard. Tuttavia, una squadra con un'alta deviazione standard potrebbe essere il tipo di squadra che segna molti punti (attacco forte) ma che lascia anche che l'altra squadra segni molti punti (difesa debole).
Cercare di sapere in anticipo quali squadre vinceranno può includere guardare le deviazioni standard delle varie "statistiche" di squadra. I numeri che sono diversi da quelli attesi possono far combaciare i punti di forza con quelli di debolezza per mostrare quali ragioni possono essere più importanti per sapere quale squadra vincerà.
Nelle corse, si misura il tempo che un pilota impiega per finire ogni giro della pista. Un pilota con una bassa deviazione standard dei tempi sul giro è più costante di un pilota con una deviazione standard più alta. Questa informazione può essere usata per capire come un pilota può ridurre il tempo per finire un giro.
Soldi
In denaro, la deviazione standard può significare il rischio che un prezzo salga o scenda (azioni, obbligazioni, proprietà, ecc.). Può anche significare il rischio che un gruppo di prezzi salga o scenda (fondi comuni gestiti attivamente, fondi comuni indicizzati o ETF). Il rischio è una ragione per prendere decisioni su cosa comprare. Il rischio è un numero che le persone possono usare per sapere quanto denaro possono guadagnare o perdere. Man mano che il rischio aumenta, il rendimento di un investimento può essere maggiore del previsto (la deviazione standard "più"). Tuttavia, un investimento può anche perdere più soldi del previsto (la deviazione standard "meno").
Per esempio, una persona doveva scegliere tra due azioni. Il titolo A negli ultimi 20 anni ha avuto un rendimento medio del 10%, con una deviazione standard di 20 punti percentuali (pp). Il titolo B negli ultimi 20 anni ha avuto un rendimento medio del 12% ma una deviazione standard più alta di 30 punti percentuali. Pensando al rischio, la persona può decidere che il titolo A è la scelta più sicura. Anche se potrebbe non guadagnare molto, probabilmente non perderà neanche molti soldi. La persona potrebbe pensare che la media più alta di 2 punti del titolo B non valga la deviazione standard aggiuntiva di 10 pp (maggiore rischio o incertezza del rendimento atteso).
Regole per i numeri normalmente distribuiti
La maggior parte delle equazioni matematiche per la deviazione standard presuppone che i numeri siano distribuiti normalmente. Ciò significa che i numeri sono distribuiti in un certo modo su entrambi i lati del valore medio. La distribuzione normale è anche chiamata distribuzione gaussiana perché è stata scoperta da Carl Friedrich Gauss. Viene spesso chiamata curva a campana perché i numeri si distribuiscono a forma di campana su un grafico.
I numeri non sono normalmente distribuiti se sono raggruppati da una parte o dall'altra del valore medio. I numeri possono essere sparsi ed essere ancora normalmente distribuiti. La deviazione standard dice quanto ampiamente i numeri sono distribuiti.

Il blu scuro è meno di una deviazione standard dalla media. Per la distribuzione normale, questo include il 68,27% dei numeri; mentre due deviazioni standard dalla media (blu medio e scuro) includono il 95,45%; tre deviazioni standard (blu chiaro, medio e scuro) includono il 99,73%; e quattro deviazioni standard rappresentano il 99,994%.
Relazione tra la media (media) e la deviazione standard
La media (media) e la deviazione standard di un insieme di dati vengono solitamente scritte insieme. Così una persona può capire qual è il numero medio e come sono distribuiti gli altri numeri del gruppo.
Il modo in cui un gruppo di numeri è distribuito può anche essere dato dal coefficiente di variazione, che è la deviazione standard divisa per la media. È un numero senza dimensione. Il coefficiente di variazione è spesso moltiplicato per 100% e scritto come percentuale.
Storia
Il termine deviazione standard fu usato per la prima volta per iscritto da Karl Pearson nel 1894, dopo averlo usato nelle conferenze. Fu come una sostituzione di nomi precedenti per la stessa idea: per esempio, Gauss usava l'errore medio.
Pagine correlate
- Accuratezza e precisione
- Dimensione del campione
Domande e risposte
D: Che cos'è la deviazione standard?
R: La deviazione standard è un numero utilizzato per indicare come le misurazioni di un gruppo si discostano dalla media (media o valore atteso).
D: Cosa significa una deviazione standard bassa?
R: Una deviazione standard bassa significa che la maggior parte dei numeri è vicina alla media.
D: Cosa significa una deviazione standard alta?
R: Una deviazione standard elevata significa che i numeri sono più sparpagliati.
D: Come si usa la deviazione standard nel denaro?
R: Nel denaro, la deviazione standard degli interessi maturati mostra quanto gli interessi maturati da una persona possano essere diversi dalla media.
D: Quando è possibile misurare solo una parte di un gruppo?
R: Molte volte è possibile misurare solo un campione o una parte di un gruppo.
D: Come viene rappresentata la deviazione standard dell'intero gruppo?
R: La deviazione standard dell'intero gruppo è rappresentata dalla lettera greca َ {\code(0144)} {displaystyle \sigma }. .
D: Come viene rappresentata la deviazione standard del campione?
R: La deviazione standard del campione è rappresentata da s {displaystyle s} .
Cerca nell'enciclopedia



