Principio di incertezza

Diagrammi

1. I fotoni, gli elettroni e altre particelle subatomiche si mettono a fuoco quando vengono sparati attraverso un grande buco, ma non sappiamo esattamente dove si trovavano a metà del loro percorso.


2. Restringendo il foro si piega il percorso delle particelle intorno ai bordi del foro (diffrazione) in modo che il fascio risultante diventi più grande e più morbido.


3. Restringere il foro aumenta la certezza di dove si trova il fotone nel mezzo, ma poi la sua direzione da lì allo schermo di rilevamento sulla destra diventa corrispondentemente più incerta. La messa a fuoco diventa sfocata. Allargando il foro i fotoni finiscono tutti al centro dello schermo di rilevamento, ma poi abbiamo meno idea di dove si trovassero quando hanno attraversato la barriera centrale.


4. Il montaggio a molla di una barriera con un piccolo foro fa passare la particella attraverso il foro, che spinge la barriera, allunga le molle, e quindi misura lo slancio. Ma poiché la barriera a molla si muove, siamo meno sicuri di dove si trovava la particella quando è passata attraverso il foro, e la diffrazione influenzerà anche la sua posizione sullo schermo di rilevamento.


5. Sospendendo la distanza centrale con le scale a molla si può misurare la quantità di moto, ma così facendo si sposta in modo imprevedibile e si perdono le informazioni sulla posizione di ogni fotone nel mezzo.


6. Questa animazione mostra una delle conseguenze importanti della natura incerta dell'universo: il tunneling quantistico degli elettroni. Guardate attentamente. Ogni volta che un po' attraversa la barriera.

Come hanno imparato gli umani a conoscere l'incertezza?

Poco dopo che Werner Heisenberg ha creato la nuova fisica quantistica, qualcosa di inaspettato è uscito proprio dalla sua matematica, l'espressione:

Δ x Δ p ≳ h 4 π {\fscx130\fscy130\frx40}Delta x π,\fscx130\fscy130\frx40}Delta p \fscy130\frx40}Delta p \fscy130\frx40}frac {\fscy130\frx40}Ah...

L'intervallo di errore in posizione (x) volte l'intervallo di errore in quantità di moto (p) è circa uguale o superiore alla costante di Planck divisa per 4π.

Questi simboli mettono in forma matematica ciò che avete già visto nelle immagini qui sopra. I simboli dicono, in modo chiaro, che non si può essere perfettamente certi di dove si trova qualcosa e dove sta andando. Se in qualsiasi momento è più chiaro dove si trova, allora si ha meno idea di dove sta andando e a che velocità. Se si è più chiari su dove sta andando e a che velocità in qualsiasi momento, allora si ha meno idea di dove si trova in questo momento.

Gli scienziati avevano già imparato perché certe sostanze emettono i caratteristici colori della luce quando sono riscaldate o comunque eccitate. Heisenberg cercava di spiegare perché questi colori hanno ciascuno una luminosità caratteristica. Non sarebbe stato sufficiente se lui e gli altri scienziati avessero detto: "Beh, è così che stanno le cose". Erano sicuri che ci doveva essere una buona ragione per queste differenze, e per il fatto che i rapporti tra le intensità delle linee luminose erano sempre gli stessi per ogni campione di un elemento.

Non aveva idea che avrebbe inciampato su un segreto nascosto della natura quando si è messo a scoprire la spiegazione dell'intensità delle linee colorate caratteristiche di ciascuno degli elementi. Lo studio della meccanica quantistica aveva già dimostrato perché l'idrogeno ha quattro linee luminose nella parte dello spettro che l'uomo può vedere. Deve essere sembrato che la prossima cosa da imparare fosse semplicemente come calcolare la loro luminosità. L'idrogeno sembrava essere il punto di partenza ovvio, dato che l'idrogeno ha solo un elettrone da trattare, e solo quattro linee nella parte visibile dello spettro. Sicuramente ci deve essere una buona ragione per cui non sono ugualmente brillanti. La spiegazione della luminosità delle linee di neon di diverso colore e degli altri elementi potrebbe aspettare.

 

Heisenberg iniziò a lavorare sulla fisica quantistica adattando le equazioni classiche per l'elettricità, che sono molto complicate all'inizio, quindi la matematica dietro il suo saggio del 1925 fu molto difficile da seguire.

Stava cercando di trovare il modo giusto per calcolare l'intensità delle linee luminose nello spettro della lampada a idrogeno. Doveva trovare una quantità correlata chiamata "ampiezza" e moltiplicare l'ampiezza per l'ampiezza (o in altre parole doveva squadrare l'ampiezza) per ottenere l'intensità che voleva. Doveva capire come esprimere l'ampiezza in un modo che tenesse conto del fatto che le lampade a idrogeno non si irradiano a tutte le frequenze, e non si irradiano attraverso una gamma continua di frequenze nella parte dello spettro che le persone possono vedere. Heisenberg trovò un nuovo e notevole modo di calcolare l'ampiezza.

La strana equazione|equazione che Heisenberg scoprì e utilizzò per fare la moltiplicazione di una quantità quantistica (ad esempio, la posizione) per un'altra (ad esempio, lo slancio) fu pubblicata in quello che è stato chiamato "il documento 'magico' di Heisenberg del luglio 1925".

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) ( n - a , n - b ) {\an8}(n,n-b)={a}^sum _{a}^, A(n,n-a)B(n-a,n-b)}(n-a,n-b)}(n-a,n-b)

La matematica di cui sopra sembra molto difficile, ma la matematica che la precede è molto più difficile ed è estremamente difficile da capire. Viene data qui solo per mostrare com'era. Il saggio di Heisenberg è un punto di riferimento storico. Molti dei fisici che hanno letto il suo saggio hanno detto che non potevano essere in disaccordo con le sue conclusioni, ma che non potevano seguire la sua spiegazione di come è arrivato a quelle conclusioni. Le equazioni iniziali utilizzate da Heisenberg riguardavano la serie di Fourier, e coinvolgevano molti fattori. Torneremo all'equazione di cui sopra perché è una sorta di ricetta per scrivere e moltiplicare le matrici.

Le nuove equazioni dovevano essere così strane e insolite perché Heisenberg descriveva un mondo strano in cui alcune cose, come le orbite degli elettroni, non diventano lentamente più grandi o più piccole. I nuovi tipi di cambiamenti comportano salti e grandi spazi vuoti tra i salti. Gli elettroni possono saltare solo tra certe orbite, e l'energia guadagnata o persa nel cambiare tra le orbite viene prodotta quando viene assorbito un fotone della giusta energia o viene prodotto un nuovo fotone della giusta energia. Se gli elettroni negli atomi di idrogeno saltano più frequentemente verso il basso (cadono) tra due particolari orbite, allora più fotoni saranno emessi a quel livello di energia, e quindi la luce prodotta a quel livello sarà la più intensa.

Era difficile fare equazioni costruite per spettri continui (quello che si vede quando si mette la luce del sole attraverso un prisma) adattare spettri che hanno solo alcuni picchi di frequenza tra i quali non c'è nulla. Quasi tutto ciò che era già stato imparato sulla luce e l'energia era stato fatto con cose grandi come candele accese o sole, e questi grandi oggetti producono tutti spettri continui. Anche se queste cose di dimensioni normali erano facili da sperimentare, c'era voluto ancora molto tempo per capire le leggi (fisiche) che le governano. Ora i fisici avevano a che fare con cose troppo piccole da vedere, cose che non producevano spettri continui, e cercavano di trovare un modo per ottenere almeno degli indizi da ciò che già conoscevano che li aiutassero a trovare le leggi di queste piccole fonti di luce, che non erano in grado di produrre spettri continui.

Le equazioni originali trattavano di una sorta di corpo vibrante che produceva un'onda, un po' come il modo in cui un'ancia in un organo produceva un'onda sonora di una frequenza caratteristica. Quindi c'era un movimento in avanti e indietro (come la vibrazione di un'ancia) e c'era un'onda emessa che poteva essere graffiata come un'onda sinusoidale. Molto di ciò che era stato scoperto in precedenza sulla fisica a livello atomico aveva a che fare con gli elettroni che si muovevano intorno ai nuclei. Quando una massa si muove in un'orbita, quando ruota intorno a una specie di mozzo, ha quello che viene chiamato "momento angolare". La quantità di moto angolare è il modo in cui qualcosa come una giostra continua a ruotare dopo che le persone hanno smesso di spingerla. La matematica usata per il calcolo delle fasi e della quantità di moto angolare è complicata. Inoltre, Heisenberg non ha mostrato tutti i suoi calcoli nel suo saggio del 1925, quindi anche i bravi matematici potrebbero avere difficoltà a compilare ciò che non ha detto.

Anche se molti fisici hanno detto di non essere riusciti a capire i vari passaggi matematici del documento di Heisenberg, un recente articolo che cerca di spiegare come Heisenberg ha ottenuto il suo risultato utilizza venti pagine piene di matematica. Anche quell'articolo non è facile da capire. La matematica è iniziata con alcune cose veramente difficili e alla fine avrebbe prodotto qualcosa di relativamente semplice che è mostrato in cima a questo articolo. Ottenere il risultato più semplice non è stato facile, e non cercheremo di mostrare il processo di passaggio da un'immagine obsoleta dell'universo alla nuova fisica quantistica. Abbiamo bisogno solo di dettagli sufficienti a mostrare che quasi appena Heisenberg ha fatto la sua scoperta una parte di come funziona l'universo che nessuno aveva mai visto prima è venuto in vista.

Heisenberg doveva essere molto eccitato ma anche molto stanco quando, a tarda notte, ha finalmente fatto la sua scoperta e ha iniziato a dimostrare a se stesso che avrebbe funzionato. Quasi subito notò qualcosa di strano, qualcosa che pensava fosse un piccolo problema fastidioso da far sparire in qualche modo. Ma si è scoperto che questo piccolo fastidio era una grande scoperta.

Heisenberg aveva lavorato per moltiplicare le ampiezze per le ampiezze, e ora Heisenberg aveva un buon modo per esprimere l'ampiezza usando la sua nuova equazione. Naturalmente stava pensando alla moltiplicazione, e a come avrebbe moltiplicato le cose che gli venivano date in termini di equazioni complicate.

Heisenberg si rese conto che, oltre all'ampiezza di quadratura, alla fine avrebbe voluto moltiplicare la posizione per lo slancio, o moltiplicare l'energia per il tempo, e sembrava che avrebbe fatto la differenza se avesse invertito l'ordine in questi nuovi casi. Heisenberg non pensava che dovesse importare se una posizione si moltiplicava per lo slancio o se si moltiplicava lo slancio per la posizione. Se fossero stati solo numeri semplici non ci sarebbe stato alcun problema. Ma erano entrambe equazioni complicate, e il modo in cui si sono ottenuti i numeri da inserire nelle equazioni si è rivelato diverso a seconda del modo in cui si è iniziato. In natura si doveva misurare la posizione e poi misurare la quantità di moto, oppure si doveva misurare la quantità di moto e poi misurare la posizione, e in matematica prevaleva la stessa situazione generale. (Vedi l'articolo di Wikipedia inglese di Heisenberg sulla meccanica delle matrici se vuoi imparare i dettagli pignoli!) Le minuscole ma fastidiose differenze tra i risultati sarebbero rimaste, non importa quanto Heisenberg desiderasse che andassero via.

All'epoca Heisenberg non riusciva a liberarsi di quel piccolo problema, ma era esausto, così consegnò il suo lavoro al suo diretto superiore, Max Born, e andò in vacanza.

Max Born era un notevole matematico che ben presto vide che l'equazione che Heisenberg gli aveva dato era una sorta di ricetta per scrivere una matrice. Il dottor Born era una delle poche persone a quel tempo interessate a questo strano tipo di matematica che la maggior parte della gente pensava non fosse molto utile. Sapeva che le matrici potevano essere moltiplicate, così facendo tutti i calcoli per la contabilità di un problema di fisica potevano essere gestiti moltiplicando una matrice per un'altra. Il solo fatto di poter mettere una procedura complicata in una forma standard e accettabile renderebbe più facile il lavoro. Potrebbe anche rendere più facile l'accettazione da parte di altre persone.

Nato era un matematico talmente bravo che si rese conto quasi subito che cambiando l'ordine di moltiplicazione delle due matrici avrebbe prodotto un risultato diverso, e i risultati sarebbero stati diversi di poco. Tale quantità sarebbe stata h/2πi. Nella vita di tutti i giorni, quella differenza sarebbe stata così piccola che non l'avremmo nemmeno vista.

Quando alcune molecole sono eccitate emettono un colore caratteristico.


Spettro dell'idrogeno


Spettro al neon


Spettro visivo completo del sole. Non ci sono lacune. Questo grafico mostra le intensità alle varie frequenze.


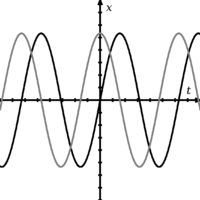
Due onde che sono fuori fase tra loro

Verso una teoria formale dell'incertezza

Ci sono voluti un paio d'anni, ma Heisenberg è riuscito a dimostrare il Principio di Incertezza, che dice che Δx × Δp = h/2, che è il numero che esce dalle equazioni originali ma lascia fuori il π e l'i che hanno a che fare con i cambiamenti di fase. Heisenberg ha spiegato di aver derivato il suo principio di incertezza da questo risultato precedente quando nel 1927 scrisse un articolo che introduceva questa teoria.

La costante scritta h, chiamata costante di Planck, è un numero misterioso che si verifica spesso, quindi dobbiamo capire cos'è questo piccolo numero. Numericamente, di solito è dato come 6,62607×10^-34 J s (joule secondi). Quindi è una quantità che coinvolge energia e tempo.

È stato scoperto quando Planck si è reso conto che l'energia di un radiatore perfetto (chiamato radiatore a corpo nero) viene emessa in unità di dimensioni definite chiamate "quanti" (il singolare di questa parola è "quantum"). L'energia irradiata viene emessa sotto forma di fotoni, e la frequenza di un fotone è proporzionale al "pugno" che emette. Sperimentiamo diverse frequenze della luce visibile come colori diversi. All'estremità violetta dello spettro, ogni fotone ha una quantità relativamente grande di energia; all'estremità rossa dello spettro ogni fotone ha una quantità relativamente piccola di energia. Il modo di calcolare la quantità di energia di un fotone è dato dall'equazione E = hν (l'energia è uguale alla costante di Planck per "nu" o frequenza).

Il principio di indeterminazione di Heisenberg Δx × Δp ≥ h ci dice che ogni volta che cerchiamo di individuare determinate coppie di numeri possiamo avvicinarci solo fino a un certo punto, e che se cerchiamo di essere più chiari su una di esse, cioè se cerchiamo di rendere Δx più piccolo in modo da avere un'idea migliore della posizione di qualcosa, allora dovremo farci restituire un numero più grande per l'altro numero della coppia, e che la quantità di cui i due sono fuori è strettamente correlata ad h.

Un'altra coppia di grandezze fisiche va secondo la relazione di incertezza: ΔE × Δt ≥ h, e questa coppia indica, tra le altre cose, che se guardiamo nello spazio interstellare, un posto dove non ci aspetteremmo di trovare nulla, e riduciamo Δt sempre più vicino a 0, allora per mantenere l'equilibrio mostrato nell'equazione ΔE deve diventare sempre più grande - e improvvisamente qualcosa con slancio può nascere solo per quel breve periodo di tempo.

Come si spiega questa indeterminatezza (mancanza di certezza)? Cosa succede nell'Universo? Si dice spesso che una nuova teoria che ha successo può fornire nuove informazioni sui fenomeni in esame. Heisenberg ha creato un modello matematico che prevedeva le intensità corrette per lo spettro luminoso dell'idrogeno, ma senza volerlo ha scoperto che alcune coppie di grandezze fisiche rivelano un'incertezza inaspettata. Fino a quel momento nessuno aveva la minima idea che le misure non potessero essere sempre più precise e accurate. Il fatto che non si potessero rendere più certe, più definite, è stata una nuova sorprendente scoperta. Molte persone non erano disposte ad accettarla.

Bohr e i suoi colleghi hanno sostenuto che fotoni, elettroni, ecc. non hanno né posizione né slancio finché non vengono misurati. Questa posizione teorica è nata dalla scoperta dell'incertezza, e non era solo una preferenza personale su cosa credere. Bohr ha detto che non sappiamo nulla di qualcosa come un fotone o un elettrone finché non lo osserviamo. Per osservare una cosa così piccola dobbiamo interagire con essa in qualche modo. Nella vita di tutti i giorni è possibile fare qualcosa come camminare accanto a un'automobile mentre si segnano i tempi in cui essa attraversa i punti su una griglia disegnata sul marciapiede. Forse il peso dell'automobile stessa deprimerà delle piccole leve nel marciapiede che spengono gli orologi attaccati a ciascuno di essi e registrano il peso dell'automobile. Alla fine avremmo una chiara registrazione di dove si trovava l'auto in vari momenti, e potremmo anche calcolare la sua direzione di avanzamento e il suo peso. Potremmo quindi conoscere, in qualsiasi momento dell'orologio, sia la sua posizione che la sua quantità di moto (la sua velocità moltiplicata per la sua massa). Non immagineremmo nemmeno che la forza necessaria per muovere le piccole leve avesse una qualche influenza sul progresso dell'automobile. Non immagineremmo nemmeno che l'automobile non abbia una posizione o una traiettoria tra i punti del marciapiede dove ci sono le leve, o che l'automobile esista in una sorta di sfocatura tridimensionale in quei momenti e si assesti solo mentre sta premendo una leva. Il mondo che conosciamo non rivela questo strano tipo di interazioni.

Per localizzare una nave in mare durante la notte più buia potremmo usare un riflettore, e quella luce non disturberebbe la posizione o la direzione di marcia della nave, ma per localizzare un elettrone con la luce sarebbe necessario colpirlo con uno o più fotoni che abbiano ciascuno uno slancio sufficiente a disturbare la posizione e la traiettoria dell'elettrone. Localizzare l'elettrone con altri mezzi significherebbe trattenerlo in una sorta di vincolo fisico che ne interromperebbe anche il movimento in avanti.

Per localizzare un fotone, il meglio che si può fare senza interrompere il suo movimento in avanti è farlo passare attraverso un foro circolare in una barriera. Se si conosce l'ora in cui il fotone è stato emesso (per esempio da un laser) e l'ora in cui il fotone arriva ad uno schermo di rilevamento come una macchina fotografica digitale, allora è possibile calcolare il tempo necessario per percorrere quella distanza e il tempo in cui il fotone è passato attraverso il foro. Tuttavia, per consentire il passaggio del fotone, il foro circolare deve avere un diametro superiore alle dimensioni del fotone. Più piccolo è il foro circolare, più ci si avvicina a conoscere l'esatta posizione del fotone mentre lo attraversa. Tuttavia, non possiamo mai sapere se il fotone è fuori centro in quel momento. Se il foro è esattamente della stessa dimensione del fotone non passerà attraverso. Man mano che il diametro del foro diminuisce, la quantità di moto o la direzione del fotone in uscita dal foro è sempre più cambiata.

Niels Bohr e i suoi colleghi sostenevano che ci si mette nei guai se si suppone che siano vere le cose troppo piccole per essere viste anche con un microscopio qualsiasi cosa di cui si abbia la prova solo sulla scala della vita quotidiana. Nella vita di tutti i giorni le cose hanno sempre una posizione precisa. Sulla scala atomica non abbiamo prove a sostegno di questa conclusione. Nella vita di tutti i giorni, le cose hanno un momento preciso in cui si verificano. Sulla scala atomica, non abbiamo prove a sostegno di questa conclusione. Nella vita di tutti i giorni, se si osserva una fabbrica dal turno di notte del primo giorno al turno di giorno del secondo e si vede un'automobile finita srotolata al molo di spedizione, non avrebbe senso dire che è impossibile dire se è stata consegnata durante il turno di notte o durante il turno di giorno. Ma sulla scala atomica possiamo mostrare casi in cui dobbiamo contare un singolo fotone come se fosse stato prodotto in due tempi. (Se questo non è abbastanza grave, possiamo anche mostrare casi in cui un singolo fotone è stato prodotto da due laser adiacenti).

Parte della difficoltà di scoprire cosa sta succedendo sulla scala atomica è che vorremmo sapere sia dove si trova qualcosa sia quale sia la sua traiettoria, e conoscere entrambe le cose per lo stesso tempo, ma non possiamo misurare sia la posizione che la traiettoria allo stesso tempo. O misuriamo la quantità di moto di un fotone o di un elettrone in una sola volta e poi, senza più ritardo del necessario, ne misuriamo la posizione, oppure cambiamo le cose e misuriamo la posizione prima e la quantità di moto seconda. Il problema è che facendo assumere al primo una forma piuttosto definita (schiacciandolo in qualche modo) aumentiamo l'incertezza della misura successiva. Se le nostre misurazioni iniziali fossero così grezze da introdurre molti errori in ciascuna di esse, allora potremmo migliorare le cose usando un tocco più leggero per ciascuna di esse, ma non riusciremmo mai ad andare oltre un certo limite di precisione.

Sappiamo dalla vita di tutti i giorni che cercare di pesare qualcosa su una bilancia da bagno posta su una lavatrice in centrifuga produce risultati imprecisi perché l'ago della bilancia si muove male. Possiamo spegnere la lavatrice. Ma per misurazioni molto accurate troviamo che i camion che passano nel quartiere fanno tremare l'ago, così possiamo mettere la bilancia su un qualcosa per isolarla dai disturbi esterni. Crediamo di poter eliminare le vibrazioni in modo da ottenere risultati accurati quanto vogliamo. Non consideriamo mai che la cosa sulla bilancia sia di per sé vibrante o che abbia uno slancio indefinito.

Parlando all'indietro rispetto al Principio di Incertezza, sembra che in realtà non ci sia una posizione e uno slancio precisi per qualsiasi cosa su scala atomica, e che gli sperimentatori possono solo forzare le cose a definirsi entro il limite stabilito dal Principio di Incertezza. Bohr e i suoi colleghi hanno solo sostenuto che non possiamo sapere nulla senza fare delle misurazioni, e quando le misurazioni sono state fatte possiamo spingere le cose nella direzione di una posizione più definita o di uno slancio più definito, ma che non possiamo ottenere l'assoluta definitezza o la certezza che vorremmo. Ma altri hanno preso sul serio questa possibilità, e hanno sostenuto che se la matematica è giusta allora non ci può essere la definizione o la certezza nel mondo dell'ultra piccolo. La natura della scienza è che la matematica è solo un modello della realtà, e non c'è garanzia che sia un modello corretto.

La matematica e le conseguenze pratiche delle cose che la matematica prevede sono così affidabili che è molto difficile non essere d'accordo, ma ciò che la matematica dice sul mondo reale ha prodotto diverse idee diverse. Tra gli scienziati che hanno lavorato con Niels Bohr a Copenhagen, il principio dell'incertezza è stato preso per significare che a livello elementare l'universo fisico non esiste in forma deterministica. Si tratta piuttosto di un insieme di probabilità o potenzialità.

In contrasto con la storia tessuta intorno alla matematica dal gruppo di Copenhagen, ci sono altre storie come "l'interpretazione dei multipli universi" che dice che ogni volta che ci sono multipli risultati possibili secondo la teoria quantistica, ogni risultato si verifica nel suo nuovo universo. Einstein sosteneva che non ci sono molteplici esiti possibili, quindi c'è un solo universo ed è determinato, o, come diceva lui, "Dio non gioca a dadi".

Se h fosse la più piccola quantità di energia possibile, allora l'equazione di base che mostra l'energia contenuta nei fotoni di varia frequenza non si equilibrerebbe. Sarebbe sbagliata.

Obiezioni contro il principio di incertezza

Albert Einstein vide che la nuova meccanica quantistica implicava una mancanza di posizione e di slancio nel tempo prima di effettuare le misure, e si oppose fermamente. Egli credeva fermamente che le cose avessero posizioni e slanci definiti prima di essere misurate, e che il fatto che misurare una di un paio di cose e disturbare la possibilità di misurare accuratamente l'altra non giustifica la mancanza di una delle due prima. Lui e due suoi colleghi hanno scritto quello che è diventato il "documento EPR". Quel documento sostiene che ci devono essere caratteristiche che determinano la posizione e lo slancio, e che se potessimo vederle, o se potessimo ottenere informazioni su di esse, allora potremmo conoscere e prevedere matematicamente la posizione e lo slancio. Per molto tempo la gente ha pensato che non ci fosse modo di provare o confutare ciò che per Einstein era un articolo di fede. L'argomento è stato molto produttivo perché ha portato a tutti gli sviluppi moderni dell'intreccio.

Matematicamente, Einstein si è dimostrato sbagliato. Nel 1964 John Stewart Bell ha sviluppato un metodo matematico per distinguere tra il comportamento di due particelle che hanno stati determinati che sono semplicemente sconosciuti ai due individui che li indagano, e due particelle che hanno stati aggrovigliati che sono indeterminati o incerti fino a quando non vengono misurati. Il suo metodo mostra che le probabilità di ottenere determinati risultati sono diverse sotto le due diverse ipotesi. Il suo lavoro si chiama teorema di Bell o disuguaglianza di Bell. Gli esperimenti hanno dimostrato che la natura si comporta come la descrive Bell.

Un'altra via verso l'incertezza

Le discussioni iniziali sul principio di indeterminazione di Heisenberg dipendevano da un modello che non considerava che le particelle di materia come gli elettroni, i protoni, ecc. hanno una lunghezza d'onda. Nel 1926 Louis de Broglie dimostrò che tutte le cose, non solo i fotoni, hanno una loro frequenza. Le cose hanno una natura ondulatoria e una natura particellare, proprio come i fotoni. Se cerchiamo di rendere l'onda di una cosa come un protone più stretta e più alta, questo renderebbe la sua posizione più chiara, ma poi lo slancio diventerebbe meno definito. Se cerchiamo di rendere più chiara la quantità di moto di un'onda, cioè di farla rimanere entro un intervallo di valori più ristretto, allora il picco dell'onda si diffonde e la sua posizione diventa meno definita.

L'onda che fa parte della descrizione di un fotone non è, in meccanica quantistica, la stessa cosa di un'onda sulla superficie dell'oceano o delle regioni di aria compressa e rarefatta che compongono le onde sonore. Queste onde hanno invece picchi o regioni ad alta ampiezza che hanno a che fare con la probabilità di trovare qualcosa in quel punto nello spazio e nel tempo. Più precisamente, è il quadrato dell'ampiezza che dà la probabilità che qualche fenomeno si manifesti.

L'onda che si applica a un fotone potrebbe essere una sinusoide pura. In tal caso, il quadrato del valore di ogni picco darebbe la probabilità di osservare il fotone in quel punto. Poiché le ampiezze delle sinusoidi sono ovunque le stesse, la probabilità di trovare il fotone in ciascuna di esse sarebbe la stessa. Quindi, in pratica, conoscere l'onda di uno di questi fotoni non darebbe un indizio su dove cercarlo. D'altra parte, lo slancio di un fotone è matematicamente correlato all'ampiezza della sua onda. Poiché in questo caso abbiamo un'onda sinusoidale pura, l'ampiezza di ogni ciclo dell'onda è la stessa e quindi c'è un solo valore di quantità di moto associato a questa onda. Non sapremmo dove il fotone colpirebbe, ma sapremmo esattamente con quanta forza colpirebbe.

Nei fasci di luce che si concentrano su un punto di uno schermo di rilevamento, le onde associate ai fotoni non sono onde sinusoidali pure. Sono invece onde con ampiezza elevata in un punto e ampiezza molto più bassa su entrambi i lati di quel picco più alto. Matematicamente è possibile analizzare una tale onda in un certo numero di onde sinusoidali diverse di diverse lunghezze d'onda. È un po' più facile visualizzare l'inverso di questo processo guardando una sinusoide iniziale di una frequenza a cui si aggiunge una seconda sinusoide di diversa lunghezza d'onda, poi una terza, poi una quarta e così via. Il risultato sarà un'onda complessa che mostra un picco alto e che contiene un gran numero di onde di diversa lunghezza d'onda e quindi di diversi momenti. In questo caso, la probabilità che il fotone appaia ad un certo punto è estremamente alta, ma la quantità di moto che esso fornisce può risultare correlata alla lunghezza d'onda di una qualsiasi delle onde componenti. In altre parole, il valore di p = ħ/λ non è più un valore unico, perché tutte le lunghezze d'onda delle "onde di diversa lunghezza d'onda" assemblate devono essere prese in considerazione.

La simulazione mostra come modellare matematicamente l'affilatura della posizione di una particella: Sovrapponete molte forme d'onda diverse sull'onda sinusoidale originale. Il centro formerà un picco sempre più alto, e il resto dei picchi sarà aumentato in numero ma diminuito in altezza perché interferiranno l'uno con l'altro. Quindi alla fine ci sono molte onde diverse nella sovrapposizione, ognuna con una diversa lunghezza d'onda e (di p = ħ/λ) una diversa quantità di moto, ma solo un picco molto alto, uno che cresce sempre più alto e più stretto e ci dà qualcosa di sempre più vicino ad una determinata posizione.

Per rendere lo slancio sempre più definito, avremmo dovuto togliere sempre di più le sinusoidi sovrapposte fino a quando non ci restava che una semplice sinusoide. In questo modo ridurremmo progressivamente l'altezza del picco centrale e aumenteremmo progressivamente le altezze dei luoghi concorrenti dove si potrebbe trovare la particella.

Quindi, quando iniziamo con un'immagine d'onda di particelle subatomiche, in genere ci occupiamo sempre di casi con picchi centrali relativamente alti e lunghezze d'onda relativamente numerose delle componenti. Non ci sarà mai una posizione esatta o una quantità di moto esatta prevista in queste circostanze. Se il modello matematico è una rappresentazione accurata del mondo reale, allora nessun fotone o altra particella subatomica ha una posizione esatta o una quantità di moto precisa. Quando misuriamo una tale particella possiamo scegliere un metodo che comprime ulteriormente il picco e lo rende più stretto, oppure possiamo scegliere un metodo che abbassa il picco e pareggia le lunghezze d'onda dei componenti. A seconda di ciò che misuriamo e di come lo misuriamo, possiamo rendere la nostra posizione più definita o possiamo restringere il nostro campo di quantità di moto. Possiamo fare attenzione nel progettare l'esperimento per evitare vari modi di far oscillare l'apparato, ma non possiamo sbarazzarci del fatto che non c'era nulla di completamente definito all'inizio.

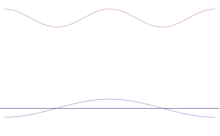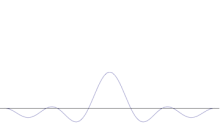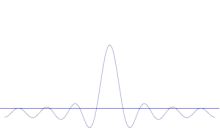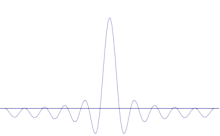
La sovrapposizione di diverse onde piane. Il pacchetto d'onda diventa sempre più localizzato con l'aggiunta di molte onde. La trasformata di Fourier è un'operazione matematica che separa un pacchetto d'onda nelle sue singole onde piane. Si noti che le onde qui mostrate sono reali solo a scopo illustrativo, mentre nella meccanica quantistica la funzione d'onda è generalmente complessa.

Influenze culturali

L'influenza più importante del Principio di indeterminazione di Heisenberg è stata sulle argomentazioni sulla libertà della volontà. Secondo le teorie della fisica classica è possibile sostenere che le leggi di causa ed effetto sono inesorabili e che una volta che l'universo è iniziato in un certo modo le interazioni di tutta la materia e l'energia che si verificheranno in futuro potrebbero essere calcolate a partire da quello stato iniziale. Poiché tutto è assolutamente il risultato di ciò che è venuto prima, hanno sostenuto, ogni decisione che un essere umano prende e ogni situazione in cui quell'essere umano entra è stata predeterminata fin dall'inizio dei tempi. Allora non abbiamo scelta in quello che facciamo.

Le persone che credono nella libertà della volontà sostengono che le leggi della meccanica quantistica non prevedono ciò che accadrà, ma solo ciò che è più e ciò che è meno probabile che accada. Pertanto ogni azione è il risultato di una serie di "lanci di monete" casuali e nessuna decisione può essere ricondotta ad un insieme di prerequisiti necessari.

Le espressioni "salto quantico" e "salto quantico" sono diventate modi ordinari di parlare delle cose. Di solito le persone intendono descrivere qualcosa come un enorme cambiamento che si verifica in un breve periodo di tempo. Il termine si applica in realtà al modo in cui un elettrone si comporta in un atomo sia quando assorbe un fotone che entra dall'esterno e quindi salta da un'orbita attorno al nucleo dell'atomo ad un'orbita più alta, sia quando emette un fotone e quindi cade da un'orbita più alta ad un'orbita più bassa. L'idea di Neils Bohr e dei suoi colleghi era che l'elettrone non si muove tra le orbite ma scompare da un'orbita e appare istantaneamente in un'altra orbita. Quindi un salto quantistico non è in realtà un qualche sconvolgente cambiamento della terra, ma un piccolo cambiamento improvviso da un dominio all'altro.

Quando gli esseri umani misurano qualche processo sulla scala subatomica e si manifesta il principio di incertezza, allora si può dire che l'azione umana ha influenzato la cosa che si stava misurando. Effettuare una misurazione destinata ad ottenere un'indicazione precisa della posizione di una particella influenzerà inevitabilmente la sua quantità di moto e qualsiasi cosa si faccia per misurare quella quantità di moto il più presto possibile dopo aver misurato la sua posizione, le probabilità di quale quantità di moto sarà scoperta non possono non essere cambiate. Quindi il principio di incertezza può spiegare alcuni tipi di interferenze prodotte dagli investigatori che influenzano i risultati di un esperimento o di un'osservazione. Tuttavia, non tutti gli effetti dell'osservatore sono dovuti agli effetti quantistici o al principio di incertezza. Il resto sono "effetti dell'osservatore" ma non effetti di incertezza quantistica.

Gli effetti dell'osservatore comprendono tutti i tipi di cose che operano alla nostra scala umana ordinaria degli eventi. Se un antropologo cerca di farsi un'idea chiara della vita in una società primitiva ma la sua presenza sconvolge la comunità che sta visitando, allora le osservazioni fatte possono essere molto fuorvianti. Tuttavia, nessuna delle interazioni rilevanti si verifica al livello descritto dalla meccanica quantistica o dal principio di incertezza.

A volte la parola "quantum" sarà usata a scopo pubblicitario per indicare qualcosa di nuovo e potente. Per esempio, il produttore di piccoli motori a benzina, Briggs e Stratton, ha una linea di motori a quattro cilindri a bassa potenza per tosaerba a benzina e simili attrezzi da giardino che chiama "Quantum".

Altre letture

• Introduzione alla teoria quantistica, pag. 115 e pag. 158

J.P. McEvoy e Oscar Zarate