Meccanica quantistica
La Meccanica Quantistica o MQ, descrive come funziona l'Universo al livello più piccolo degli atomi. È anche chiamata "fisica quantistica" o "teoria quantistica". Quantum è la parola latina per "quanto", e la meccanica è l'area della scienza che si occupa del movimento. Un quantum di energia è una quantità specifica di energia, e la Meccanica Quantistica descrive come questa energia si muove e interagisce a livello sub-atomico.
Gli atomi erano considerati i più piccoli elementi costitutivi della materia, ma la scienza moderna ha dimostrato che esistono particelle ancora più piccole, come protoni, neutroni ed elettroni. La MQ è la parte della fisica che descrive il funzionamento delle particelle che compongono gli atomi.
La MQ ci dice anche come funzionano le onde elettromagnetiche (come la luce). Gran parte della fisica e della chimica moderne possono essere descritte e comprese usando le regole matematiche della meccanica quantistica.
La matematica utilizzata per studiare le particelle subatomiche e le onde elettromagnetiche è molto complessa perché agiscono in modi molto strani.
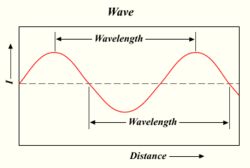
La lunghezza d'onda di un'onda di luce
Onde e fotoni
I fotoni sono particelle molto più piccole degli atomi e dei protoni ed elettroni; infatti, non hanno alcuna massa. I fotoni sono come "pacchetti" o pacchetti di energia. Le fonti di luce come le candele o i laser sparano fuori (o "emettono") luce in pezzi chiamati fotoni.
Più fotoni spara una lampada, più luminosa è la luce. La luce è una forma di energia che si comporta come le onde nell'acqua o le onde radio. La distanza tra la cima di un'onda e la cima dell'onda successiva è chiamata "lunghezza d'onda". Ogni fotone trasporta una certa quantità, o "quantum", di energia a seconda della sua lunghezza d'onda.
Il colore di una luce dipende dalla sua lunghezza d'onda. Il colore viola (il colore più basso o più interno dell'arcobaleno) ha una lunghezza d'onda di circa 400 nm ("nanometri") che è 0,00004 centimetri o 0,000016 pollici. I fotoni con lunghezza d'onda di 10-400 nm sono chiamati luce ultravioletta (o UV). Tale luce non può essere vista dall'occhio umano. All'altra estremità dello spettro, la luce rossa è di circa 700 nm. La luce infrarossa è di circa 700 nm a 300.000 nm. Gli occhi umani non sono sensibili neanche alla luce infrarossa.
Le lunghezze d'onda non sono sempre così piccole. Le onde radio hanno lunghezze d'onda più lunghe. Le lunghezze d'onda per una radio FM possono essere di diversi metri di lunghezza (per esempio, le stazioni che trasmettono su 99.5 FM stanno emettendo energia radio con una lunghezza d'onda di circa 3 metri, che è circa 10 piedi). Ogni fotone ha una certa quantità di energia legata alla sua lunghezza d'onda. Più corta è la lunghezza d'onda di un fotone, maggiore è la sua energia. Per esempio, un fotone ultravioletto ha più energia di un fotone infrarosso.
La lunghezza d'onda e la frequenza (il numero di volte che l'onda cresce al secondo) sono inversamente proporzionali, il che significa che una lunghezza d'onda più lunga avrà una frequenza più bassa, e viceversa. Se il colore della luce è l'infrarosso (frequenza più bassa della luce rossa), ogni fotone può riscaldare ciò che colpisce. Quindi, se una forte lampada a infrarossi (una lampada di calore) è puntata su una persona, questa si sentirà calda, o addirittura bollente, a causa dell'energia immagazzinata nei molti fotoni. La superficie della lampada a infrarossi può anche diventare abbastanza calda da bruciare qualcuno che può toccarla. Gli esseri umani non possono vedere la luce infrarossa, ma possiamo sentire la radiazione sotto forma di calore. Per esempio, una persona che cammina vicino a un edificio di mattoni che è stato riscaldato dal sole sentirà il calore dell'edificio senza doverlo toccare.
Le formulazioni matematiche della meccanica quantistica sono astratte. Una funzione matematica, chiamata funzione d'onda, fornisce informazioni sull'ampiezza di probabilità (il quadrato dell'ampiezza di probabilità è la probabilità) di posizione, quantità di moto e altre proprietà fisiche di una particella. Molti dei risultati della meccanica quantistica non sono facilmente visualizzabili in termini di meccanica classica.
La luce ultravioletta ha una frequenza superiore a quella della luce violetta, tanto che non è nemmeno nella gamma della luce visibile. Ogni fotone nella gamma ultravioletta ha molta energia, abbastanza per ferire le cellule della pelle e causare una scottatura. Infatti, la maggior parte delle forme di scottatura non sono causate dal calore; sono causate dall'alta energia dei raggi UV del sole che danneggiano le cellule della pelle. Anche frequenze più alte di luce (o radiazioni elettromagnetiche) possono penetrare più in profondità nel corpo e causare ancora più danni. I raggi X hanno così tanta energia che possono andare in profondità nel corpo umano e uccidere le cellule. Gli esseri umani non possono vedere o sentire la luce ultravioletta o i raggi X. Possono sapere di essere stati sotto una luce ad alta frequenza solo quando hanno un'ustione da radiazioni. Le aree in cui è importante uccidere i germi spesso usano lampade ultraviolette per distruggere batteri, funghi, ecc. I raggi X sono talvolta usati per uccidere le cellule cancerogene.
La meccanica quantistica è iniziata quando si è scoperto che una certa frequenza significa una certa quantità di energia. L'energia è proporzionale alla frequenza (E ∝ f). Più alta è la frequenza, più energia ha un fotone e più danni può fare. La meccanica quantistica è cresciuta in seguito per spiegare la struttura interna degli atomi. La meccanica quantistica spiega anche il modo in cui un fotone può interferire con se stesso, e molte altre cose mai immaginate nella fisica classica.

Il nero a sinistra è l'ultravioletto (alta frequenza); il nero a destra è l'infrarosso (bassa frequenza).
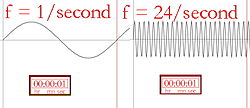
Descrizione pittorica della frequenza
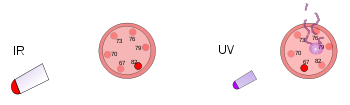
A sinistra, un termometro di plastica è sotto una lampada di calore luminoso. Questa radiazione infrarossa riscalda ma non danneggia il termometro. A destra, un altro termometro di plastica viene colpito da una luce ultravioletta a bassa intensità. Questa radiazione danneggia ma non riscalda il termometro.
Quantizzazione
Max Planck scoprì la relazione tra frequenza ed energia. Nessuno prima di lui aveva mai intuito che la frequenza è direttamente proporzionale all'energia (ciò significa che se una delle due raddoppia, lo fa anche l'altra). Sotto quelle che sono chiamate unità naturali, allora il numero che rappresenta la frequenza di un fotone rappresenterebbe anche la sua energia. L'equazione sarebbe quindi:
E = f
il che significa che l'energia è uguale alla frequenza.
Ma per come era cresciuta la fisica, non c'era una connessione naturale tra le unità usate per misurare l'energia e le unità comunemente usate per misurare il tempo (e quindi la frequenza). Così la formula che Planck elaborò per far uscire i numeri giusti fu:
E = h × f
o, l'energia è uguale a h per la frequenza. Questa h è un numero chiamato costante di Planck dal nome del suo scopritore.
La meccanica quantistica si basa sulla conoscenza che un fotone di una certa frequenza significa un fotone di una certa quantità di energia. Oltre a questa relazione, un tipo specifico di atomo può emettere solo certe frequenze di radiazione, quindi può anche emettere solo fotoni che hanno certe quantità di energia.
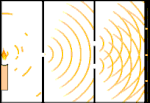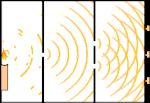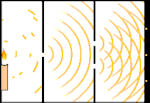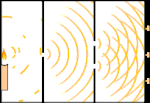
Esperimento della doppia fenditura: la luce va dalla sorgente luminosa a sinistra alle frange (segnate nel bordo nero) a destra.
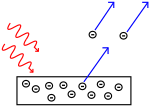
Effetto fotoelettrico: i fotoni colpiscono il metallo e gli elettroni vengono spinti via.
Storia
Isaac Newton pensava che la luce fosse fatta di cose molto piccole che oggi chiameremmo particelle (le chiamava "corpuscoli"). Christiaan Huygens pensava che la luce fosse fatta di onde. Gli scienziati pensavano che una cosa non può essere una particella e un'onda allo stesso tempo.
Gli scienziati fecero degli esperimenti per scoprire se la luce fosse fatta di particelle o di onde. Scoprirono che entrambe le idee erano giuste - la luce era in qualche modo sia onde che particelle. L'esperimento della doppia fenditura eseguito da Thomas Young dimostrò che la luce doveva agire come un'onda. L'effetto fotoelettrico scoperto da Albert Einstein dimostrò che la luce doveva agire come particelle che portavano specifiche quantità di energia, e che le energie erano legate alle loro frequenze. Questo risultato sperimentale è chiamato "dualità onda-particella" nella meccanica quantistica. Più tardi, i fisici scoprirono che tutto si comporta sia come un'onda che come una particella, non solo la luce. Tuttavia, questo effetto è molto più piccolo negli oggetti grandi.
Ecco alcune delle persone che hanno scoperto le parti fondamentali della meccanica quantistica: Max Planck, Albert Einstein, Satyendra Nath Bose, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, John von Neumann e Richard Feynman. Hanno svolto il loro lavoro nella prima metà del XX secolo.

Da sinistra a destra: Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, Richard Feynman.
Oltre Planck
Le formule e le idee della meccanica quantistica furono fatte per spiegare la luce che proviene dall'idrogeno incandescente. La teoria quantistica dell'atomo doveva anche spiegare perché l'elettrone rimane nella sua orbita, cosa che altre idee non erano in grado di spiegare. In base alle idee più vecchie, l'elettrone avrebbe dovuto cadere verso il centro dell'atomo perché all'inizio era tenuto in orbita dalla sua stessa energia, ma avrebbe perso rapidamente la sua energia mentre girava nella sua orbita. (Questo perché si sapeva che gli elettroni e altre particelle cariche emettono luce e perdono energia quando cambiano velocità o girano).
Le lampade a idrogeno funzionano come le luci al neon, ma le luci al neon hanno il loro gruppo unico di colori (e frequenze) di luce. Gli scienziati hanno imparato che potevano identificare tutti gli elementi dai colori della luce che producono. Solo che non riuscivano a capire come venivano determinate le frequenze.
Poi, un matematico svizzero di nome Johann Balmer scoprì un'equazione che diceva quale sarebbe stato λ (lambda, per la lunghezza d'onda):
λ = B ( n 2 n 2 - 4 ) n = 3 , 4 , 5 , 6 {\displaystyle \lambda =B\left({\frac {n^{2}}{n^{2}-4}}} destra)\qquad \qquad n=3,4,5,6}
dove B è un numero che Balmer ha determinato essere uguale a 364,56 nm.
Questa equazione funzionava solo per la luce visibile di una lampada a idrogeno. Ma più tardi, l'equazione fu resa più generale:
1 λ = R ( 1 m 2 - 1 n 2 ) , {displaystyle {{frac {1}{lambda }}=R\sinistra({frac {1}{m^{2}}}-{frac {1}{n^{2}}} destra),}
dove R è la costante di Rydberg, pari a 0,0110 nm-1, e n deve essere maggiore di m.
Mettendo diversi numeri per m e n, è facile prevedere le frequenze per molti tipi di luce (ultravioletta, visibile e infrarossa). Per vedere come funziona, vai su Hyperphysics e vai giù oltre il centro della pagina. (Usa H = 1 per l'idrogeno).
Nel 1908, Walter Ritz realizzò il principio di combinazione di Ritz che mostra come certi intervalli tra le frequenze continuano a ripetersi. Questo si rivelò importante per Werner Heisenberg diversi anni dopo.
Nel 1905, Albert Einstein utilizzò l'idea di Planck per dimostrare che un raggio di luce è composto da un flusso di particelle chiamate fotoni. L'energia di ogni fotone dipende dalla sua frequenza. L'idea di Einstein è l'inizio dell'idea della meccanica quantistica che tutte le particelle subatomiche come elettroni, protoni, neutroni e altri sono onde e particelle allo stesso tempo. (Vedi l'immagine dell'atomo con l'elettrone come onda nell'atomo). Questo ha portato a una teoria sulle particelle subatomiche e le onde elettromagnetiche chiamata dualità onda-particella. Questo è dove le particelle e le onde non erano né l'una né l'altra, ma avevano certe proprietà di entrambe.
Nel 1913, Niels Bohr ebbe l'idea che gli elettroni potessero occupare solo certe orbite intorno al nucleo di un atomo. Secondo la teoria di Bohr, i numeri chiamati m e n nell'equazione sopra potrebbero rappresentare delle orbite. La teoria di Bohr diceva che gli elettroni potevano iniziare in una certa orbita m e finire in una certa orbita n, o un elettrone poteva iniziare in una certa orbita n e finire in una certa orbita m, quindi se un fotone colpisce un elettrone, la sua energia sarà assorbita e l'elettrone si sposterà in un'orbita superiore a causa di quell'energia extra. Secondo la teoria di Bohr, se un elettrone cade da un'orbita superiore a un'orbita inferiore, allora dovrà cedere energia sotto forma di un fotone. L'energia del fotone sarà uguale alla differenza di energia tra le due orbite, e l'energia di un fotone gli fa avere una certa frequenza e colore. La teoria di Bohr forniva una buona spiegazione di molti aspetti dei fenomeni subatomici, ma non riusciva a rispondere al perché ciascuno dei colori della luce prodotta dall'idrogeno incandescente (e dal neon incandescente o da qualsiasi altro elemento) ha una luminosità propria, e le differenze di luminosità sono sempre le stesse per ogni elemento.
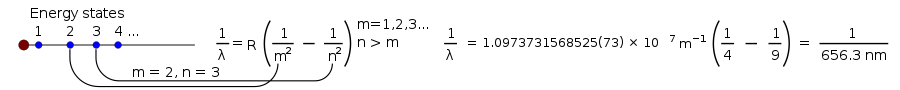
Quando Niels Bohr presentò la sua teoria, la maggior parte delle cose sulla luce prodotta da una lampada a idrogeno erano note, ma gli scienziati non riuscivano ancora a spiegare la luminosità di ciascuna delle linee prodotte dall'idrogeno incandescente.
Werner Heisenberg si incaricò di spiegare la luminosità o "intensità" di ogni linea. Non poteva usare nessuna regola semplice come quella di Balmer. Dovette usare la matematica molto difficile della fisica classica che calcola tutto in termini di cose come la massa (peso) di un elettrone, la carica (forza elettrica statica) di un elettrone e altre piccole quantità. La fisica classica aveva già delle risposte per la luminosità delle bande di colore che una lampada a idrogeno produce, ma la teoria classica diceva che ci doveva essere un arcobaleno continuo, e non quattro bande di colore separate. La spiegazione di Heisenberg è:
C'è una legge che dice quali frequenze di luce l'idrogeno incandescente produrrà. Deve prevedere frequenze distanziate quando gli elettroni coinvolti si muovono tra orbite vicine al nucleo (centro) dell'atomo, ma deve anche prevedere che le frequenze si avvicineranno sempre di più man mano che osserviamo ciò che l'elettrone fa nel muoversi tra orbite sempre più lontane. Prevede anche che le differenze di intensità tra le frequenze si avvicinano sempre di più man mano che ci allontaniamo. Dove la fisica classica dà già le risposte giuste con una serie di equazioni, la nuova fisica deve dare le stesse risposte ma con equazioni diverse.
La fisica classica usa i metodi del matematico francese Fourier per fare un'immagine matematica del mondo fisico, e usa collezioni di curve lisce che vanno insieme per fare una curva liscia che dà, in questo caso, intensità per la luce di tutte le frequenze da una certa luce. Ma non è giusto perché quella curva liscia appare solo a frequenze più alte. Alle frequenze più basse, ci sono sempre punti isolati e niente collega i punti. Così, per fare una mappa del mondo reale, Heisenberg ha dovuto fare un grande cambiamento. Doveva fare qualcosa per scegliere solo i numeri che corrispondessero a ciò che si vedeva in natura. A volte la gente dice che ha "indovinato" queste equazioni, ma non stava facendo congetture alla cieca. Ha trovato ciò che gli serviva. I numeri che calcolava mettevano dei punti su un grafico, ma non c'era nessuna linea tracciata tra i punti. E fare un "grafico" solo di punti per ogni serie di calcoli avrebbe sprecato molta carta e non avrebbe ottenuto nulla. Heisenberg ha trovato un modo per prevedere in modo efficiente le intensità per diverse frequenze e per organizzare queste informazioni in modo utile.
Solo usando la regola empirica data sopra, quella che Balmer ha iniziato e Rydberg ha migliorato, possiamo vedere come ottenere una serie di numeri che aiuterebbero Heisenberg a ottenere il tipo di immagine che voleva:
La regola dice che quando l'elettrone si sposta da un'orbita all'altra, guadagna o perde energia, a seconda che si stia allontanando dal centro o avvicinando ad esso. Così possiamo mettere queste orbite o livelli di energia come titoli lungo la parte superiore e laterale di una griglia. Per ragioni storiche l'orbita più bassa si chiama n, e l'orbita successiva si chiama n - a, poi viene n - b, e così via. È confuso il fatto che abbiano usato numeri negativi quando gli elettroni stavano effettivamente guadagnando energia, ma questo è solo il modo in cui è.
Poiché la regola di Rydberg ci dà delle frequenze, possiamo usare questa regola per mettere dei numeri a seconda di dove va l'elettrone. Se l'elettrone parte da n e finisce a n, allora non è andato da nessuna parte, quindi non ha guadagnato e non ha perso energia. Quindi la frequenza è 0. Se l'elettrone parte da n-a e finisce a n, allora è caduto da un'orbita superiore a un'orbita inferiore. Se lo fa, allora perde energia, e l'energia che perde si presenta come un fotone. Il fotone ha una certa quantità di energia, e, che è legata a una certa frequenza f dall'equazione e = h f. Quindi sappiamo che un certo cambiamento di orbita produrrà una certa frequenza della luce, f. Se l'elettrone parte da n e finisce a n - a, significa che è passato da un'orbita inferiore a un'orbita superiore. Questo accade solo quando un fotone di una certa frequenza ed energia arriva dall'esterno, viene assorbito dall'elettrone e gli dà la sua energia, e questo è ciò che fa uscire l'elettrone verso un'orbita superiore. Quindi, per dare un senso a tutto, scriviamo quella frequenza come un numero negativo. C'era un fotone con una certa frequenza e ora è stato portato via.
Quindi possiamo fare una griglia come questa, dove f(a←b) indica la frequenza coinvolta quando un elettrone passa dallo stato energetico (orbita) b allo stato energetico a (di nuovo, le sequenze sembrano al contrario, ma questo è il modo in cui sono state scritte originariamente):
Griglia di f
| Stati dell'elettrone | n | n-a | n-b | n-c | .... | |
| n | f(n←n) | f(n←n-a) | f(n←n-b) | f(n←n-c) | ..... | |
| n-a | f(n-a←n) | f(n-a←n-a) | f(n-a←n-b) | f(n-a←n-c) | ..... | |
| n-b | f(n-b←n) | f(n-b←n-a) | f(n-b←n-b) | f(n-b←n-c) | ..... | |
| transizione .... | ..... | ..... | ..... | ..... |
Heisenberg non ha fatto le griglie in questo modo. Ha solo fatto i calcoli che gli avrebbero permesso di ottenere le intensità che stava cercando. Ma per farlo doveva moltiplicare due ampiezze (quanto alta misura un'onda) per calcolare l'intensità. (Nella fisica classica, l'intensità è uguale all'ampiezza al quadrato). Fece una strana equazione per gestire questo problema, scrisse il resto del suo documento, lo consegnò al suo capo e andò in vacanza. Il dottor Born guardò la sua strana equazione e gli sembrò un po' folle. Deve essersi chiesto: "Perché Heisenberg mi ha dato questa cosa strana? Perché deve fare così?". Poi si rese conto che stava guardando un progetto di qualcosa che conosceva già molto bene. Era abituato a chiamare matrice la griglia o la tabella che potevamo scrivere facendo, per esempio, tutta la matematica delle frequenze. E la strana equazione di Heisenberg era una regola per moltiplicarne due insieme. Max Born era un matematico molto, molto bravo. Sapeva che poiché le due matrici (griglie) che venivano moltiplicate rappresentavano cose diverse (come la posizione (x,y,z) e la quantità di moto (mv), per esempio), allora quando si moltiplica la prima matrice per la seconda si ottiene una risposta e quando si moltiplica la seconda matrice per la prima matrice si ottiene un'altra risposta. Anche se non conosceva la matematica delle matrici, Heisenberg aveva già visto questo problema delle "risposte diverse" e lo aveva infastidito. Ma il dottor Born era un matematico così bravo che vide che la differenza tra la prima moltiplicazione della matrice e la seconda moltiplicazione della matrice coinvolgeva sempre la costante di Planck, h, moltiplicata per la radice quadrata di uno negativo, i. Così in pochi giorni dalla scoperta di Heisenberg avevano già la matematica di base per quello che Heisenberg amava chiamare il "principio di indeterminazione". Con "indeterminato" Heisenberg intendeva che qualcosa come un elettrone non è semplicemente inchiodato finché non viene inchiodato. È un po' come una medusa che è sempre in giro e non può stare "in un posto" a meno che non la si uccida. Più tardi, la gente ha preso l'abitudine di chiamarlo "principio di indeterminazione di Heisenberg", che ha fatto commettere a molte persone l'errore di pensare che gli elettroni e cose del genere siano davvero "da qualche parte" ma che siamo solo incerti nella nostra mente. Questa idea è sbagliata. Non è quello di cui parlava Heisenberg. Avere problemi a misurare qualcosa è un problema, ma non è il problema di cui parlava Heisenberg.
L'idea di Heisenberg è molto difficile da afferrare, ma possiamo renderla più chiara con un esempio. Per prima cosa, inizieremo a chiamare queste griglie "matrici", perché presto avremo bisogno di parlare di moltiplicazione di matrici.
Supponiamo di iniziare con due tipi di misure, posizione (q) e quantità di moto (p). Nel 1925, Heisenberg scrisse un'equazione come questa:
Y ( n , n - b ) = ∑ a p ( n , n - a ) q ( n - a , n - b ) {\displaystyle Y(n,n-b)=\sum _{a}^{\},p(n,n-a)q(n-a,n-b)} 
Lui non lo sapeva, ma questa equazione fornisce un modello per scrivere due matrici (griglie) e per moltiplicarle. Le regole per moltiplicare una matrice per un'altra sono un po' confuse, ma ecco le due matrici secondo lo schema, e poi il loro prodotto:
Matrice di p
| Stati dell'elettrone | n-a | n-b | n-c | .... | |
| n | p(n←n-a) | p(n←n-b) | p(n←n-c) | ..... | |
| n-a | p(n-a←n-a) | p(n-a←n-b) | p(n-a←n-c) | ..... | |
| n-b | p(n-b←n-a) | p(n-b←n-b) | p(n-b←n-c) | ..... | |
| transizione .... | ..... | ..... | ..... | ..... |
Matrice di q
| Stati dell'elettrone | n-b | n-c | n-d | .... | |
| n-a | q(n-a←n-b) | q(n-a←n-c) | q(n-a←n-d) | ..... | |
| n-b | q(n-b←n-b) | q(n-b←n-c) | q(n-b←n-d) | ..... | |
| n-c | q(n-c←n-b) | q(n-c←n-c) | q(n-c←n-d) | ..... | |
| transizione .... | ..... | ..... | ..... | ..... |
La matrice per il prodotto delle due matrici di cui sopra, come specificato dalla relativa equazione nel documento di Heisenberg del 1925, è:
| Stati dell'elettrone | n-b | n-c | n-d | ..... |
| n | A | ..... | ..... | ..... |
| n-a | ..... | B | ..... | ..... |
| n-b | ..... | ..... | C | ..... |
Dove:
A=p(n←n-a)*q(n-a←n-b)+p(n←n-b)*q(n-b←n-b)+p(n←n-c)*q(n-c←n-b)+ .....
B=p(n-a←n-a)*q(n-a←n-c)+p(n-a←n-b)*q(n-b←n-c)+p(n-a←n-c)*q(n-c←n-c)+ .....
C=p(n-b←n-a)*q(n-a←n-d)+p(n-b←n-b)*q(n-b←n-d)+p(n-b←n-c)*q(n-d←n-d)+ .....
e così via.
Se le matrici fossero invertite, si otterrebbero i seguenti valori:
A=q(n←n-a)*p(n-a←n-b)+q(n←n-b)*p(n-b←n-b)+q(n←n-c)*p(n-c←n-b)+.....
B=q(n-a←n-a)*p(n-a←n-c)+q(n-a←n-b)*p(n-b←n-c)+q(n-a←n-c)*p(n-c←n-c)+.....
C=q(n-b←n-a)*p(n-a←n-d)+q(n-b←n-b)*p(n-b←n-d)+q(n-b←n-c)*p(n-d←n-d)+ .....
e così via.
Nota come cambiare l'ordine di moltiplicazione cambia i numeri, passo dopo passo, che vengono effettivamente moltiplicati.

Luce visibile emessa dall'idrogeno incandescente. (Lunghezze d'onda in nanometri).
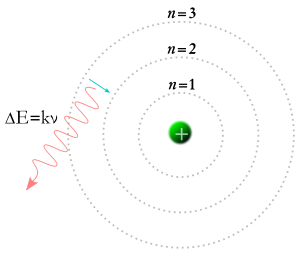
Un elettrone cade nell'orbita inferiore e viene creato un fotone.
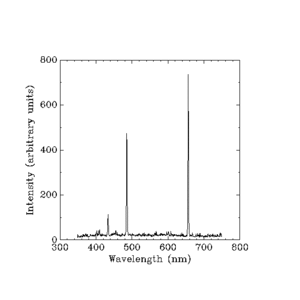
Intensità distanziate in unità arbitrarie
Oltre Heisenberg
Il lavoro di Werner Heisenberg sembrava rompere un ingorgo. Molto presto, molti altri modi diversi di spiegare le cose vennero da persone come Louis de Broglie, Max Born, Paul Dirac, Wolfgang Pauli ed Erwin Schrödinger. Il lavoro di ognuno di questi fisici è una storia a sé. La matematica usata da Heisenberg e dalle persone precedenti non è molto difficile da capire, ma le equazioni sono diventate rapidamente molto complicate quando i fisici hanno guardato più profondamente nel mondo atomico.
Altri misteri
All'inizio della meccanica quantistica, Albert Einstein suggerì che se fosse stata giusta, la meccanica quantistica avrebbe significato che ci sarebbe stata una "azione spettrale a distanza". Si scoprì che la meccanica quantistica aveva ragione, e che ciò che Einstein aveva usato come motivo per rifiutare la meccanica quantistica si verificava realmente. Questo tipo di "connessione spettrale" tra certi eventi quantistici è ora chiamato "entanglement quantistico".
Quando un esperimento mette insieme due cose (fotoni, elettroni, ecc.), devono poi condividere una descrizione comune in meccanica quantistica. Quando sono poi separati, mantengono la stessa descrizione meccanica quantistica o "stato". Nel diagramma, una caratteristica (per esempio, lo spin "su") è disegnata in rosso, e il suo compagno (per esempio, lo spin "giù") è disegnato in blu. La banda viola significa che quando, per esempio, due elettroni sono messi insieme la coppia condivide entrambe le caratteristiche. Quindi entrambi gli elettroni potrebbero mostrare sia spin verso l'alto che verso il basso. Quando poi vengono separati, uno rimanendo sulla Terra e uno andando su qualche pianeta della stella Alpha Centauri, hanno ancora entrambi gli spin. In altre parole, ognuno di loro può "decidere" di mostrarsi come un elettrone con spin-up o un elettrone con spin-down. Ma se più tardi qualcuno misura l'altro, questo deve "decidere" di mostrarsi come avente lo spin opposto.
Einstein sostenne che su una distanza così grande era folle pensare che forzare un elettrone a mostrare il suo spin avrebbe poi in qualche modo fatto mostrare all'altro elettrone una caratteristica opposta. Disse che i due elettroni dovevano essere spin-up o spin-down da sempre, ma che la meccanica quantistica non poteva prevedere quale caratteristica avesse ciascun elettrone. Non essere in grado di prevedere, essendo solo in grado di guardare uno dei due con l'esperimento giusto, significava che la meccanica quantistica non poteva rendere conto di qualcosa di importante. Pertanto, disse Einstein, la meccanica quantistica aveva un grande buco. La meccanica quantistica era incompleta.
Più tardi, si scoprì che gli esperimenti dimostravano che era Einstein ad avere torto.
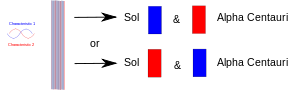
Due particelle entangled sono separate: una sulla Terra e una portata su qualche pianeta lontano. Misurare una di esse la costringe a "decidere" quale ruolo assumere, e l'altra deve poi assumere l'altro ruolo ogni volta che (dopo) viene misurata.
Principio di indeterminazione di Heisenberg
Nel 1925, Werner Heisenberg descrisse il principio di indeterminazione, che dice che più sappiamo su dove si trova una particella, meno possiamo sapere su quanto velocemente sta andando e in quale direzione. In altre parole, più sappiamo della velocità e della direzione di qualcosa di piccolo, meno possiamo sapere della sua posizione. I fisici di solito parlano della quantità di moto in queste discussioni invece di parlare di velocità. La quantità di moto è solo la velocità di qualcosa in una certa direzione per la sua massa.
Il principio di indeterminazione di Heisenberg dice che non possiamo mai conoscere sia la posizione che la quantità di moto di una particella. Poiché la luce è una particella abbondante, viene usata per misurare altre particelle. L'unico modo per misurarla è far rimbalzare l'onda luminosa sulla particella e registrare i risultati. Se si usa un fascio di luce ad alta energia, o ad alta frequenza, possiamo dire con precisione dove si trova, ma non possiamo dire quanto velocemente stava andando. Questo perché il fotone ad alta energia trasferisce energia alla particella e ne cambia la velocità. Se usiamo un fotone a bassa energia, possiamo dire a che velocità sta andando, ma non dove si trova. Questo perché stiamo usando la luce con una lunghezza d'onda più lunga. La lunghezza d'onda più lunga significa che la particella potrebbe essere ovunque lungo il tratto dell'onda.
Il principio dice anche che ci sono molte coppie di misure per le quali non possiamo conoscerle entrambe su nessuna particella (una cosa molto piccola), per quanto ci proviamo. Più impariamo su una di queste coppie, meno possiamo sapere sull'altra.
Persino Albert Einstein aveva problemi ad accettare un concetto così bizzarro, e in un noto dibattito disse: "Dio non gioca a dadi". A questo, il fisico danese Niels Bohr rispose notoriamente: "Einstein, non dire a Dio cosa fare".
Usi della MQ
Gli elettroni circondano il nucleo di ogni atomo. I legami chimici collegano gli atomi per formare le molecole. Un legame chimico collega due atomi quando gli elettroni sono condivisi tra questi atomi. Quindi la MQ è la fisica del legame chimico e della chimica. La MQ ci aiuta a capire come sono fatte le molecole e quali sono le loro proprietà.
La MQ può anche aiutarci a capire cose grandi, come le stelle e persino l'intero universo. La MQ è una parte molto importante della teoria su come l'universo è iniziato, chiamata Big Bang.
Tutto ciò che è fatto di materia è attratto da altra materia a causa di una forza fondamentale chiamata gravità. La teoria di Einstein che spiega la gravità è chiamata teoria della relatività generale. Un problema della fisica moderna è che alcune conclusioni della MQ non sembrano concordare con la teoria della relatività generale.
La MQ è la parte della fisica che può spiegare perché tutta la tecnologia elettronica funziona come funziona. Così la MQ spiega come funzionano i computer, perché i computer sono macchine elettroniche. Ma i progettisti del primo hardware dei computer intorno al 1950 o 1960 non avevano bisogno di pensare alla MQ. Anche i progettisti di radio e televisori dell'epoca non pensavano alla MQ. Tuttavia, la progettazione dei circuiti integrati più potenti e delle tecnologie di memoria dei computer degli ultimi anni richiede la MQ.
La MQ ha anche reso possibili tecnologie come:
Perché la MQ è difficile da imparare
La MQ è un argomento impegnativo per diverse ragioni:
- La MQ spiega le cose in modo molto diverso da quello che impariamo sul mondo quando siamo bambini.
- La comprensione della MQ richiede più matematica dell'algebra e del semplice calcolo. Richiede anche l'algebra delle matrici, i numeri complessi, la teoria della probabilità e le equazioni differenziali parziali.
- I fisici non sono sicuri di cosa ci dicano alcune delle equazioni della MQ sul mondo reale.
- La MQ suggerisce che gli atomi e le particelle subatomiche si comportano in modi strani, completamente diversi da qualsiasi cosa che vediamo nella nostra vita quotidiana.
- La MQ descrive cose che sono estremamente piccole, quindi non possiamo vederne alcune senza un'attrezzatura speciale, e non possiamo vederne affatto molte.
La MQ descrive la natura in un modo che è diverso da come pensiamo di solito alla scienza. Ci dice quanto è probabile che alcune cose accadano, piuttosto che dirci che certamente accadranno.
Un esempio è l'esperimento della doppia fenditura di Young. Se spariamo singoli fotoni (singole unità di luce) da un laser su un foglio di pellicola fotografica, vedremo una singola macchia di luce sulla pellicola sviluppata. Se mettiamo un foglio di metallo in mezzo, e facciamo due fessure molto strette nel foglio, quando spariamo molti fotoni sul foglio di metallo, e questi devono passare attraverso le fessure, allora vedremo qualcosa di notevole. Lungo tutto il foglio di pellicola sviluppata vedremo una serie di bande luminose e scure. Possiamo usare la matematica per dire esattamente dove saranno le bande luminose e quanto era luminosa la luce che le ha generate, cioè possiamo dire in anticipo quanti fotoni cadranno su ogni banda. Ma se rallentiamo il processo e vediamo dove atterra ogni fotone sullo schermo, non possiamo mai dire in anticipo dove apparirà il prossimo. Possiamo sapere con certezza che è molto probabile che un fotone colpisca la banda luminosa centrale, e che diventa sempre meno probabile che un fotone si presenti su bande sempre più lontane dal centro. Quindi sappiamo per certo che le bande saranno più luminose al centro e diventeranno sempre più fioche lontano. Ma non sappiamo mai con certezza quale fotone andrà in quale banda.
Una delle strane conclusioni della teoria QM è l'effetto "gatto di Schrödinger". Certe proprietà di una particella, come la sua posizione, la velocità di movimento, la direzione del movimento e lo "spin", non possono essere parlate finché qualcosa non le misura (un fotone che rimbalza su un elettrone conterebbe come una misura della sua posizione, per esempio). Prima della misurazione, la particella si trova in una "sovrapposizione di stati", in cui le sue proprietà hanno molti valori allo stesso tempo. Schrödinger disse che la meccanica quantistica sembrava dire che se qualcosa (come la vita o la morte di un gatto) fosse determinato da un evento quantistico, allora il suo stato sarebbe determinato dallo stato che risulta dall'evento quantistico, ma solo nel momento in cui qualcuno guarda lo stato dell'evento quantistico. Nel tempo prima che lo stato dell'evento quantistico venga guardato, forse "il gatto vivo e il gatto morto (perdonate l'espressione) [sono] mescolati o spalmati in parti uguali".
Costante di Planck ridotta
La gente spesso usa il simbolo ℏ {displaystyle \hbar } 

Esempio
La particella in un pozzo 1-dimensionale è l'esempio più semplice che mostra che l'energia di una particella può avere solo valori specifici. Si dice che l'energia è "quantizzata". Il pozzo ha energia potenziale zero all'interno di un intervallo e ha energia potenziale infinita ovunque fuori da quell'intervallo. Per il caso 1-dimensionale nella 
- ℏ 2 2 m d 2 ψ d x 2 = E ψ . E ψ = E ψ. }
Usando le equazioni differenziali, possiamo vedere che ψ {displaystyle \psi } 
ψ = A e i k x + B e - i k x E = ℏ 2 k 2 2 m {\displaystyle \psi =Ae^{ikx}+Be^{-ikx}};\frac {\frac {\frac {\frac}k^{2}}{2m}}
o
ψ = C sin k x + D cos k x {displaystyle \psi =C\sin kx+D\cos kx\; } 
Le pareti della scatola significano che la funzione d'onda deve avere una forma speciale. La funzione d'onda della particella deve essere zero ogni volta che le pareti sono infinitamente alte. Ad ogni parete:
ψ = 0 a t x = 0 , x = L {\displaystyle \psi =0\;\mathrm {at} \;\mathrm;x=0,\;x=L}
Considerare x = 0
- sin 0 = 0, cos 0 = 1. Per soddisfare ψ = 0 {displaystyle \scriptstyle \psi =0\; }
il termine cos deve essere rimosso. Quindi D = 0
Ora considera: ψ = C sin k x {\displaystyle \scriptstyle \psi =C\sin kx\; }
- a x = L, ψ = C sin k L = 0 {\displaystyle \scriptstyle \psi =C\sin kL=0\; }
- Se C = 0 allora ψ = 0 {displaystyle \scriptstyle \psi =0\; }
per tutti gli x. Questa soluzione non è utile.
- quindi sin kL = 0 deve essere vero, dandoci
k L = n π n = 1 , 2 , 3 , 4 , 5 , . . . {\displaystyle kL=n\pi \\i};\i};\i};n=1,2,3,4,5,...\i};}
Possiamo vedere che n {displaystyle n}
Pagine correlate
- Onda elettromagnetica
- Elettrone
- Fotone
- Entanglement quantistico
- Equazione di Schrödinger
Domande e risposte
D: Che cos'è la meccanica quantistica?
R: La meccanica quantistica è una branca della fisica che spiega come funziona l'universo su una scala più piccola degli atomi. È anche conosciuta come fisica quantistica o teoria quantistica.
D: Che cosa significa il termine "quantum"?
R: Il termine "quantum" deriva dal latino e significa "quanto". Un quanto di energia è la minima quantità possibile (o la minima quantità extra), e la meccanica quantistica descrive come questa energia si muove o interagisce.
D: Cosa sono le particelle subatomiche?
R: Le particelle subatomiche sono particelle che compongono gli atomi, come protoni, neutroni ed elettroni. Sono ancora più piccole degli atomi.
D: Come la meccanica quantistica descrive il funzionamento di queste particelle?
R: La meccanica quantistica fornisce regole matematiche per studiare le particelle subatomiche e le onde elettromagnetiche, al fine di comprendere il loro comportamento e le interazioni reciproche.
D: Cos'è la dualità onda-particella?
R: La dualità onda-particella si riferisce al fatto che sia le particelle che le onde possono comportarsi l'una come l'altra - non sono due entità distinte, ma piuttosto qualcosa di simile a entrambe combinate in un unico fenomeno.
D: Come si può descrivere la fisica moderna utilizzando la meccanica quantistica?
R: La fisica e la chimica moderne possono essere spiegate applicando loro le regole matematiche della meccanica quantistica.
Cerca nell'enciclopedia







