Il principio di indeterminazione di Heisenberg

Confusione con effetto osservatore

Storicamente, il principio di incertezza è stato confuso con un effetto in qualche modo simile in fisica, chiamato effetto osservatore. Questo dice che le misurazioni di alcuni sistemi non possono essere effettuate senza influenzare i sistemi. Heisenberg ha offerto un tale effetto di osservazione a livello quantistico come "spiegazione" fisica dell'incertezza quantistica.

Tuttavia, è ormai chiaro che il principio dell'incertezza è una proprietà di tutti i sistemi simili alle onde. Esso sorge nella meccanica quantistica semplicemente a causa della natura ondulatoria della materia di tutti gli oggetti quantici. Quindi, il principio di incertezza afferma in realtà una proprietà fondamentale dei sistemi quantistici, e non è un'affermazione sul successo osservazionale della tecnologia attuale. "Misurazione" non significa solo un processo al quale partecipa un fisico osservatore, ma piuttosto qualsiasi interazione tra gli oggetti classici e gli oggetti quantistici indipendentemente da qualsiasi osservatore.

L'idea di indeterminazione

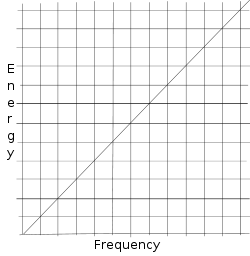
Il principio dell'incertezza derivava dalla meccanica della matrice di Werner Heisenberg. Max Planck sapeva già che l'energia di un'unità di luce è proporzionale alla frequenza di quell'unità di luce ( E ∝ ν {\an8}, e che la sua quantità di energia può essere espressa in termini familiari come il joule utilizzando una costante di proporzionalità. La costante che ha dato al mondo si chiama ora costante di Planck ed è rappresentata dalla lettera h. Quando si usano le matrici per esprimere la meccanica quantistica, spesso è necessario moltiplicare due matrici per ottenere una terza matrice che dia la risposta che il fisico sta cercando di trovare. Ma moltiplicando una matrice come P (per la quantità di moto) per una matrice come X (per la posizione) si ottiene una matrice di risposta diversa da quella che si ottiene moltiplicando X per P. Il risultato della moltiplicazione di P per X e X per P e poi confrontando le due matrici si ottiene sempre la costante di Planck come fattore. Il numero usato per scrivere la costante di Planck dipenderà sempre dal sistema di misura in uso. (Con un certo sistema di misura, il suo valore numerico è uno.) La pendenza della linea nel diagramma a destra che mostra il rapporto frequenza/energia dipenderà anche dal sistema di misura scelto.

I seguenti diagrammi mostrano cosa succede quando si cerca di misurare sia la posizione che lo slancio.

Il risultato pratico di questa scoperta matematica è che quando un fisico rende la posizione più chiara, lo slancio diventa meno chiaro, e che quando il fisico rende lo slancio più chiaro, la posizione diventa meno chiara. Heisenberg diceva che le cose sono "indeterminate", e ad altre persone piaceva dire che erano "incerte". Ma la matematica dimostra che sono le cose del mondo ad essere indeterminate o "sfocate", e non che gli esseri umani sono incerti su ciò che sta succedendo.

Foro largo, messa a fuoco nitida


Restringendo il divario si aumenta la certezza di dove si trova il fotone nel mezzo, ma poi la sua direzione da lì alla schermata di rilevamento sulla destra diventa corrispondentemente più incerta.


Foro stretto, fuoco diffuso


Sospendendo lo spazio al centro con le molle si può misurare la quantità di moto, ma si sposta in modo imprevedibile e si perde l'informazione sulla posizione del fotone nel mezzo.


Il foro montato a molla misura la quantità di moto

Mettere l'indeterminazione in forma matematica

Qui mostreremo la prima equazione che ha dato l'idea di base dimostrata in seguito nel principio di indeterminazione di Heisenberg.

La carta rivoluzionaria di Heisenberg del 1925 non utilizza e non menziona nemmeno le matrici. Il grande successo di Heisenberg fu lo "schema che era in grado, in linea di principio, di determinare in modo univoco le qualità fisiche rilevanti (frequenze di transizione e ampiezze)" della radiazione dell'idrogeno.

Dopo che Heisenberg scrisse il suo saggio, lo diede a uno dei suoi insegnanti per sistemarlo e andò in vacanza. Max Born rimase perplesso dalle equazioni e dalle equazioni di non pendolarismo che anche Heisenberg pensava fossero un problema. Dopo alcuni giorni Born si rese conto che queste equazioni erano indicazioni per scrivere le matrici. Le matrici erano nuove e strane, anche per i matematici dell'epoca, ma come fare matematica con esse era già chiaramente noto. Lui e pochi altri lavorarono a tutto in forma di matrice prima che Heisenberg tornasse dal suo tempo libero, e nel giro di pochi mesi la nuova meccanica quantistica in forma di matrice diede loro la base per un altro lavoro.

Max Born ha visto che quando le matrici che rappresentano pq e qp sono state calcolate non sarebbero state uguali. Heisenberg aveva già visto la stessa cosa in termini del suo modo originale di scrivere le cose, e Heisenberg potrebbe aver indovinato ciò che era quasi immediatamente ovvio per Born - che la differenza tra le matrici di risposta per pq e per qp avrebbe sempre comportato due fattori che venivano dalla matematica originale di Heisenberg: La costante h e i di Planck, che è la radice quadrata di quella negativa. Così l'idea stessa di quello che Heisenberg preferiva chiamare il "principio di indeterminazione" (solitamente noto come principio di incertezza) si nascondeva nelle equazioni originali di Heisenberg.

Heisenberg aveva osservato i cambiamenti che avvengono in un atomo quando un elettrone cambia il suo livello di energia e quindi si avvicina al centro del suo atomo o si allontana dal suo centro, e, soprattutto, le situazioni in cui un elettrone cade in uno stato di energia inferiore in due fasi. Max Born ha spiegato come ha preso la strana "ricetta" di Heisenberg per trovare il prodotto, C, di un qualche cambiamento in un atomo dal livello di energia n al livello di energia n-b, che consisteva nel prendere la somma di moltiplicare un cambiamento in qualcosa chiamato A (che potrebbe essere, per esempio, la frequenza di qualche fotone) prodotto da un cambiamento di energia di un elettrone nell'atomo tra lo stato di energia n e lo stato di energia n-a) per un cambiamento successivo in qualcosa chiamato B (che potrebbe essere, per esempio, l'ampiezza di un cambiamento) prodotto da un altro cambiamento nello stato di energia da n-a a n-b):

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) ( n - a , n - b ) {\an8}(n,n-b)={a}^sum _{a}^, A(n,n-a)B(n-a,n-b)}(n-a,n-b)}(n-a,n-b)

e ha scoperto qualcosa di rivoluzionario:

Considerando ...esempi...[Heisenberg] trovò questa regola.... Questo nell'estate del 1925. Heisenberg... si congedò... e mi consegnò il suo giornale per la pubblicazione ....

La regola della moltiplicazione di Heisenberg non mi ha lasciato pace, e dopo una settimana di intenso pensiero e di prove, mi sono improvvisamente ricordato di una teoria algebrica ....Tali matrici quadratiche sono abbastanza familiari ai matematici e sono chiamate matrici, in associazione con una precisa regola di moltiplicazione. Applicai questa regola alla condizione quantistica di Heisenberg e scoprii che era d'accordo per gli elementi diagonali. Era facile indovinare quali dovevano essere gli elementi rimanenti, cioè, nulli; e subito mi si presentò davanti la strana formula

Q P - P Q = i h 2 π {\ih}{QP-PQ={\frac {ih}{2\pi }}}}
Il simbolo Q è la matrice per lo spostamento, P è la matrice per la quantità di moto, i sta per la radice quadrata di quella negativa, e h è la costante di Planck.

Più tardi, Heisenberg mise la sua scoperta in un'altra forma matematica:

Δ x Δ p ≥ ℏ 2 ^displaystyle ^Delta x^,^Delta p^geq ^frac ^^hbar ^2 ^^

(Il simbolo specialeℏ ℏ, che si chiama "h-bar", o 'costante di Planks ridotta', è uguale a h 2 π, h 2 π, frac. .)

La matematica è un modo di descrivere le cose che accadono nel mondo reale. Si potrebbe immaginare che sarebbe facile ottenere sia la posizione esatta di qualcosa che la sua massa esatta, il percorso e la velocità allo stesso tempo. Tuttavia, in realtà bisogna fare due cose per ottenere la risposta. Se si misura la posizione e lo slancio di un proiettile che è bloccato in una scogliera di una grande montagna da qualche parte, è una cosa semplice. La montagna non sembra andare da nessuna parte, e nemmeno il proiettile. Quindi la sua posizione è nota e la sua velocità è 0, quindi anche la sua quantità di moto è 0. Ma se il proiettile si trova da qualche parte tra una pistola e un bersaglio, sarà difficile ottenere la sua posizione in un dato momento. Il meglio che possiamo fare è fotografarlo con una macchina fotografica con un otturatore molto veloce. Ma una sola pressione dell'otturatore darebbe solo una cosa, la posizione del proiettile al momento t. Per ottenere lo slancio potremmo mettere un blocco di paraffina sulla traiettoria del proiettile e misurare come il blocco di paraffina si è mosso quando ha fermato il proiettile. Oppure, se conosciamo la massa del proiettile, potremmo fare una sequenza di due immagini, calcolare la velocità conoscendo la differenza tra le due posizioni del proiettile e il tempo tra le sue due apparizioni. In ogni caso, dobbiamo misurare la massa e la posizione e il tempo tra le due apparenze. Si finisce per fare almeno due misure per arrivare a x e p. In questo caso dobbiamo scegliere quale misura fare per prima e quale per seconda. Sembra che non faccia alcuna differenza in quale ordine vengono effettuate le nostre misurazioni. Misurare la massa del proiettile e poi misurare due volte la sua posizione, o misurare due volte la posizione del proiettile e poi recuperare il proiettile e misurare la sua massa non farebbe alcuna differenza, vero? Dopotutto, non abbiamo fatto nulla al proiettile quando lo pesiamo o quando ne facciamo delle fotografie.

Su scala molto piccola quando misuriamo qualcosa come un elettrone, tuttavia, ogni misurazione fa qualcosa. Se prima misuriamo la posizione, poi cambiamo il suo momemtum nel processo. Se misuriamo prima lo slancio dell'elettrone, poi cambiamo la sua posizione nel processo. La nostra speranza sarebbe quella di misurare uno di essi e poi misurare l'altro prima che qualcosa cambi, ma la nostra stessa misurazione fa un cambiamento, e il meglio che possiamo sperare di fare è ridurre al minimo l'energia che contribuiamo all'elettrone misurandolo. Quella quantità minima di energia ha la costante di Planck come uno dei suoi fattori.

L'incertezza va oltre la matematica della matrice

Il principio di incertezza di Heisenberg è stato trovato nelle prime equazioni della "nuova" fisica quantistica, e la teoria è stata data usando la matematica della matrice. Tuttavia, il principio di incertezza è un dato di fatto della natura, e si manifesta in altri modi di parlare di fisica quantistica, come le equazioni di Erwin Schrödinger.

L'indeterminazione in natura, non l'incertezza dell'uomo

Ci sono stati due modi molto diversi di guardare a ciò che Heisenberg ha scoperto: Alcuni pensano che le cose che accadono in natura siano "determinate", cioè che le cose accadano secondo una regola precisa e se potessimo sapere tutto quello che dobbiamo sapere potremmo sempre dire cosa accadrà dopo. Altri pensano che le cose che accadono in natura sono guidate solo dalla probabilità, e possiamo sapere solo come si comporteranno le cose in media, ma lo sappiamo con molta precisione.

Il fisico John Stewart Bell ha scoperto un modo per dimostrare che il primo modo non può essere corretto. Il suo lavoro si chiama teorema di Bell o disuguaglianza di Bell.

Cultura popolare

L'espressione "salto quantico" o "salto quantico" è stata presa per indicare un grande e trasformativo cambiamento, ed è spesso usata in espressioni iperboliche dai politici e dalle campagne di vendita dei mass media. In meccanica quantistica è usata per descrivere il passaggio di un elettrone da un'orbita attorno al nucleo di un atomo a qualsiasi altra orbita, superiore o inferiore.

A volte la parola "quantum" è usata nei nomi dei prodotti commerciali e delle imprese. Per esempio, Briggs e Stratton produce molti tipi di piccoli motori a benzina per tosaerba, frese rotative e altre macchine così piccole. Uno dei loro nomi di modelli è "Quantum".

Poiché il principio di incertezza ci dice che certe misurazioni a livello atomico non possono essere effettuate senza disturbare altre misurazioni, alcuni individui usano questa idea per descrivere casi nel mondo umano in cui l'attività di un osservatore cambia la cosa che viene osservata. Un antropologo può andare in qualche luogo lontano per imparare come vivono le persone, ma il fatto che una strana persona del mondo esterno sia lì ad osservarli può cambiare il modo in cui queste persone agiscono.

Le cose che le persone fanno osservando le cose che cambiano ciò che si osserva sono casi di effetto Osservatore. Alcune cose che le persone fanno causano cambiamenti a livello di atomi molto piccoli e sono casi di incertezza o indeterminatezza come descritto da Heisenberg. Il principio dell'incertezza mostra che c'è sempre un limite a quanto piccolo possiamo fare certe coppie di misure come la posizione e la velocità o la traiettoria e la quantità di moto. L'effetto osservatore dice che a volte ciò che le persone fanno nell'osservare le cose, ad esempio, imparare a conoscere una colonia di formiche scavando con gli attrezzi da giardino, può avere grandi effetti che cambiano ciò che cercavano di imparare.