Teorema dei quattro colori

Formulazione esatta del problema

Intuitivamente, il teorema dei quattro colori può essere dichiarato come "data una qualsiasi separazione di un piano in regioni contigue, chiamata mappa, le regioni possono essere colorate usando al massimo quattro colori in modo che non ci siano due regioni adiacenti che abbiano lo stesso colore". Per poter risolvere correttamente il problema, è necessario chiarire alcuni aspetti: In primo luogo, tutti i punti che appartengono a tre o più paesi devono essere ignorati. In secondo luogo, mappe bizzarre con regioni di area finita e perimetro infinito possono richiedere più di quattro colori.

Ai fini del teorema ogni "paese" deve essere una regione semplicemente connessa, o contigua. Nel mondo reale, questo non è vero: L'Alaska come parte degli Stati Uniti, Nakhchivan come parte dell'Azerbaigian e Kaliningrad come parte della Russia non sono contigue. Poiché il territorio di un determinato paese deve essere dello stesso colore, quattro colori potrebbero non essere sufficienti. Per esempio, si consideri una mappa semplificata, come quella mostrata a sinistra: In questa mappa, le due regioni contrassegnate con la lettera A appartengono allo stesso paese e devono essere dello stesso colore. Questa mappa richiede quindi cinque colori, poiché le due regioni A insieme sono contigue ad altre quattro regioni, ognuna delle quali è contigua a tutte le altre. Se A avesse solo tre regioni, potrebbero essere necessari sei o più colori. In questo modo, è possibile realizzare mappe che necessitano di un numero arbitrariamente elevato di colori. Una costruzione simile vale anche se si usa un solo colore per tutti i corpi d'acqua, come è usuale sulle mappe reali.

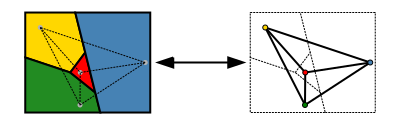
Una versione più facile da dichiarare del teorema utilizza la teoria dei grafici. L'insieme delle regioni di una mappa può essere rappresentato in modo più astratto come un grafico non orientato che ha un vertice per ogni regione e un bordo per ogni coppia di regioni che condividono un segmento di confine. Questo grafico è planare: può essere disegnato nel piano senza attraversamenti ponendo ogni vertice in un punto scelto arbitrariamente all'interno della regione a cui corrisponde, e disegnando i bordi come curve che conducono senza attraversamenti all'interno di ogni regione dalla posizione del vertice ad ogni punto di confine condiviso della regione. Al contrario, qualsiasi grafico planare può essere formato da una mappa in questo modo. Nella terminologia grafico-teorica, il teorema dei quattro colori afferma che i vertici di ogni grafico planare possono essere colorati al massimo con quattro colori, in modo che non ci siano due vertici adiacenti che abbiano lo stesso colore, o per abbreviare, "ogni grafico planare è quadricromiabile" (Thomas 1998, p. 849; Wilson 2002).

Esempio di mappa dell'Azerbaigian con regioni non contigue


Questa mappa non può essere colorata con quattro colori

Storia

Il primo a nominare il problema fu Francis Guthrie, nel 1852. All'epoca era uno studente di legge in Inghilterra. Scoprì che gli servivano almeno quattro colori per colorare una mappa delle contee d'Inghilterra. Augustus de Morgan parlò per la prima volta del problema, in una lettera che scrisse a Rowan Hamliton nell'agosto del 1852. Nella lettera, de Morgan chiede se quattro colori sono davvero sufficienti per colorare una mappa, in modo tale che i paesi che si trovano uno accanto all'altro ottengano colori diversi.

Il matematico inglese Arthur Cayley presentò il problema alla società matematica a Londra nel 1878. Nel giro di un anno, Alfred Kempe trovò quella che sembrava una prova del problema. Undici anni dopo, nel 1890, Percy Heawood dimostrò che la prova di Alfred era sbagliata. Peter Guthrie Tait presentò un altro tentativo di prova nel 1880. Ci vollero undici anni per dimostrare che anche la prova di Tait non funzionava. Nel 1891, Julius Petersen riuscì a dimostrarlo. Quando falsificò la prova di Cayley, Kempe mostrò anche una prova per un problema che chiamò teorema dei cinque colori. Il teorema dice che qualsiasi mappa di questo tipo può essere colorata con non più di cinque colori. Ci sono due restrizioni: Primo, ogni paese è contiguo, non ci sono esclamazioni. La seconda restrizione è che i paesi devono avere un confine comune; se toccano solo in un punto, possono essere colorati con lo stesso colore. Anche se la prova di Kempe era sbagliata, ha usato alcune delle idee che in seguito avrebbero permesso una prova corretta.

Negli anni Sessanta e Settanta, Heinrich Heesch ha sviluppato un primo schizzo di una prova al computer. Kenneth Appel e Wolfgang Haken hanno migliorato questo schizzo nel 1976 (Robertson et al. 1996). Essi sono stati in grado di ridurre il numero di casi che avrebbero dovuto essere testati al 1936; una versione successiva è stata fatta in una versione successiva che si basava sul test di soli 1476 casi. Ogni caso doveva essere testato da un computer (Appel & Haken 1977).

Nel 1996, Neil Robertson, Daniel Sanders, Paul Seymour e Robin Thomas migliorarono il metodo e ridussero il numero di casi da testare a 663. Anche in questo caso, ogni caso doveva essere testato al computer.

Nel 2005, Georges Gonthier e Benjamin Werner hanno sviluppato una prova formale. Si trattava di un miglioramento, perché permetteva di utilizzare per la prima volta un software a prova di teorema. Il software utilizzato si chiama Coq.

Il teorema dei quattro colori è il primo grande problema matematico che è stato dimostrato con l'aiuto di un computer. Poiché la prova non può essere fatta da un essere umano, alcuni matematici non l'hanno riconosciuto come corretto. Per verificare la prova, è necessario affidarsi ad un software e ad un hardware che funzioni correttamente per convalidare la prova. Poiché la prova è stata fatta da un computer, non è nemmeno molto elegante.

Tentativi che si sono rivelati sbagliati

Il teorema dei quattro colori è stato famoso per aver attirato un gran numero di prove false e confutazioni nella sua lunga storia. All'inizio, il New York Times si è rifiutato di riferire sulle prove di Appel-Haken. Il giornale lo fece per motivi di politica; temeva che la prova sarebbe stata mostrata falsa come quelle precedenti (Wilson 2002, p. 209). Alcune prove hanno richiesto molto tempo, prima di poter essere falsificate: Per le prove di Kempe e Tait falsificarle ci volle più di un decennio.

I controcampioni più semplici cercano generalmente di creare una regione che tocca tutte le altre. Questo costringe le regioni rimanenti ad essere colorate con solo tre colori. Poiché il teorema dei quattro colori è vero, questo è sempre possibile; tuttavia, poiché la persona che disegna la mappa è concentrata su una sola grande regione, non si accorge che le regioni rimanenti possono essere colorate con tre colori.

Questo trucco può essere generalizzato: Se i colori di alcune regioni di una mappa vengono scelti in anticipo, diventa impossibile colorare le regioni rimanenti in modo tale che in totale vengano utilizzati solo quattro colori. Qualcuno che verifica il controesempio potrebbe non pensare che sia necessario cambiare il colore di queste regioni. Questo farà sembrare valido il controesempio, anche se non lo è.

Forse un effetto alla base di questo comune malinteso è il fatto che la restrizione del colore non è transitiva: una regione deve solo essere colorata in modo diverso dalle regioni che tocca direttamente, non le regioni che toccano le regioni che tocca. Se questa fosse la restrizione, i grafici planari richiederebbero un numero arbitrariamente elevato di colori.

Altre false confutazioni violano i presupposti del teorema in modi inaspettati, come l'utilizzo di una regione che ha più parti scollegate, o il fatto di non permettere alle regioni dello stesso colore di toccare un punto.

Colorare le mappe politiche

Nella vita reale, molti paesi hanno delle exclavi o delle colonie. Poiché appartengono al paese, devono essere colorate con lo stesso colore della nazione madre. Ciò significa che di solito sono necessari più di quattro colori per colorare una mappa di questo tipo. Quando i matematici parlano del grafico associato al problema, dicono che non è planare. Anche se è facile controllare se un grafico è planare, trovare il minor numero di colori necessari per colorarlo è molto difficile. È NP-completo, che è uno dei problemi più difficili che esistono. Il minor numero di colori necessari per colorare un grafico è noto come il suo numero cromatico. Molti dei problemi che si presentano quando si cerca di risolvere il teorema dei quattro colori sono legati alla matematica discreta. Per questo motivo, spesso si usano metodi della topologia algebrica.

Estensione alle mappe "non piatte

Il teorema dei quattro colori richiede che la "mappa" si trovi su una superficie piana, quello che i matematici chiamano un piano. Nel 1890, Percy John Heawood creò quella che oggi viene chiamata congettura di Heawood: Si pone la stessa domanda del teorema dei quattro colori, ma per qualsiasi oggetto topologico. Per esempio, un toro può essere colorato con un massimo di sette colori. La congettura di Heawood dà una formula che funziona per tutti questi oggetti, tranne che per la bottiglia di Klein.