Tensione superficiale
La tensione superficiale è un effetto in cui la superficie di un liquido è forte. La superficie può sostenere un peso, e la superficie di una goccia d'acqua tiene insieme la goccia, a forma di palla. Alcune piccole cose possono galleggiare su una superficie a causa della tensione superficiale, anche se normalmente non potrebbero galleggiare. Alcuni insetti (per esempio i cavalieri d'acqua) possono correre sulla superficie dell'acqua per questo motivo. Questa proprietà è causata dalle molecole del liquido che sono attratte l'una dall'altra (coesione), ed è responsabile di molti dei comportamenti dei liquidi.
La tensione superficiale ha la dimensione della forza per unità di lunghezza, o dell'energia per unità di superficie. Le due cose sono equivalenti, ma quando ci si riferisce all'energia per unità di superficie, si usa il termine energia superficiale, che è un termine più generale nel senso che si applica anche ai solidi e non solo ai liquidi.
Nella scienza dei materiali, la tensione superficiale è usata sia per lo stress superficiale che per l'energia libera superficiale.
Causa
Le forze coesive tra le molecole del liquido causano la tensione superficiale. Nella massa del liquido, ogni molecola è tirata ugualmente in ogni direzione dalle molecole di liquido vicine, risultando in una forza netta di zero. Le molecole in superficie non hanno altre molecole su tutti i lati e quindi sono tirate verso l'interno. Questo crea una certa pressione interna e costringe le superfici del liquido a contrarsi alla superficie minima.
La tensione superficiale è responsabile della forma delle gocce liquide. Anche se facilmente deformabili, le gocce d'acqua tendono ad essere tirate in una forma sferica dalle forze coesive dello strato superficiale. In assenza di altre forze, compresa la gravità, le gocce di quasi tutti i liquidi sarebbero perfettamente sferiche. La forma sferica minimizza la necessaria "tensione di parete" dello strato superficiale secondo la legge di Laplace.
Un altro modo di vederla è in termini di energia. Una molecola in contatto con un vicino è in uno stato di energia più basso che se fosse sola (non in contatto con un vicino). Le molecole interne hanno tutti i vicini che possono avere, ma alle molecole di confine mancano i vicini (rispetto alle molecole interne). Quindi, le molecole di confine hanno un'energia più alta. Affinché il liquido minimizzi il suo stato energetico, il numero di molecole di confine a più alta energia deve essere minimizzato. La quantità minimizzata di molecole di confine si traduce in un'area superficiale minimizzata.
Come risultato della minimizzazione dell'area superficiale, una superficie assumerà la forma più liscia possibile. Qualsiasi curvatura nella forma della superficie si traduce in un'area maggiore e in una maggiore energia. Quindi, la superficie spingerà indietro contro qualsiasi curvatura più o meno nello stesso modo in cui una palla spinta in salita spingerà indietro per minimizzare la sua energia potenziale gravitazionale.
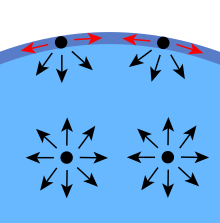
Diagramma delle forze sulle molecole in un liquido
La tensione superficiale impedisce alla graffetta di immergersi.
Effetti nella vita quotidiana
Acqua
Lo studio dell'acqua mostra diversi effetti della tensione superficiale:
A. L'acqua piovana forma delle perle sulla superficie di una superficie cerosa, come una foglia. L'acqua aderisce debolmente alla cera e fortemente a se stessa, così l'acqua si raggruppa in gocce. La tensione superficiale dà loro la forma quasi sferica, perché una sfera ha il più piccolo rapporto possibile tra superficie e volume.
B. La formazione di gocce avviene quando una massa di liquido viene allungata. L'animazione mostra l'acqua che aderisce al rubinetto guadagnando massa fino a quando viene allungata fino a un punto in cui la tensione superficiale non può più legarla al rubinetto. Quindi si separa e la tensione superficiale forma la goccia in una sfera. Se un flusso d'acqua scorresse dal rubinetto, il flusso si romperebbe in gocce durante la sua caduta. La gravità allunga il flusso, poi la tensione superficiale lo stringe in sfere.
C. Gli oggetti più densi dell'acqua continuano a galleggiare quando l'oggetto non è bagnabile e il suo peso è abbastanza piccolo da essere sostenuto dalle forze derivanti dalla tensione superficiale. Per esempio, i cavalieri d'acqua usano la tensione superficiale per camminare sulla superficie di uno stagno. La superficie dell'acqua si comporta come una pellicola elastica: le zampe dell'insetto causano rientranze nella superficie dell'acqua, aumentandone la superficie.
D. La separazione di olio e acqua (in questo caso, acqua e cera liquida) è causata da una tensione superficiale tra liquidi dissimili. Questo tipo di tensione superficiale è chiamato "tensione di interfaccia", ma la sua fisica è la stessa.
E. Le lacrime di vino sono la formazione di gocce e rivoli sul lato di un bicchiere contenente una bevanda alcolica. La sua causa è una complessa interazione tra le diverse tensioni superficiali di acqua ed etanolo. È indotta da una combinazione di modifica della tensione superficiale dell'acqua da parte dell'etanolo insieme all'etanolo che evapora più velocemente dell'acqua.
· 
A. Perline d'acqua su una foglia
· 
B. Acqua che gocciola da un rubinetto
· 
C. I corridori d'acqua rimangono in cima al liquido a causa della tensione superficiale
· 
D. Lampada a lava con interazione tra liquidi dissimili; acqua e cera liquida
· 
E. Foto che mostra il fenomeno delle "lacrime di vino".
Tensioattivi
La tensione superficiale è visibile in altri fenomeni comuni, specialmente quando si usano tensioattivi per diminuirla:
- Le bolle di sapone hanno superfici molto grandi con pochissima massa. Le bolle in acqua pura sono instabili. L'aggiunta di tensioattivi, tuttavia, può avere un effetto stabilizzante sulle bolle (vedi effetto Marangoni). Si noti che i tensioattivi riducono effettivamente la tensione superficiale dell'acqua di un fattore tre o più.
- Le emulsioni sono un tipo di soluzione in cui la tensione superficiale gioca un ruolo. Minuscoli frammenti di olio sospesi in acqua pura si assemblano spontaneamente in masse molto più grandi. Ma la presenza di un tensioattivo fornisce una diminuzione della tensione superficiale, che permette la stabilità di minuscole goccioline di olio nella massa d'acqua (o viceversa).
Fisica di base
Due definizioni
La tensione superficiale, rappresentata dal simbolo γ è definita come la forza lungo una linea di lunghezza unitaria, dove la forza è parallela alla superficie ma perpendicolare alla linea. Un modo per immaginare questo è quello di immaginare una pellicola di sapone piatta delimitata su un lato da un filo teso di lunghezza L. Il filo sarà tirato verso l'interno della pellicola da una forza pari a 2 γ {displaystyle \scriptstyle \gamma } 
L (il fattore 2 è perché la pellicola di sapone ha due lati, quindi due superfici). La tensione superficiale si misura quindi in forze per unità di lunghezza. La sua unità SI è newton per metro, ma si usa anche l'unità cgs di dyne per cm. Un dyn/cm corrisponde a 0,001 N/m.
Una definizione equivalente, utile in termodinamica, è il lavoro fatto per unità di superficie. Come tale, per aumentare la superficie di una massa di liquido di una quantità, δA, una quantità di lavoro, γ {displaystyle \scriptstyle \gamma } δA, è necessaria. Questo lavoro è immagazzinato come energia potenziale. Di conseguenza la tensione superficiale può essere misurata anche nel sistema SI come joule per metro quadrato e nel sistema cgs come ergs per cm2. Poiché i sistemi meccanici cercano di trovare uno stato di minima energia potenziale, una goccia libera di liquido assume naturalmente una forma sferica, che ha la minima area superficiale per un dato volume.
L'equivalenza della misura dell'energia per unità di superficie con la forza per unità di lunghezza può essere dimostrata dall'analisi dimensionale.
Curvatura della superficie e pressione
Se nessuna forza agisce normalmente a una superficie in tensione, la superficie deve rimanere piatta. Ma se la pressione su un lato della superficie differisce dalla pressione sull'altro lato, la differenza di pressione per l'area della superficie risulta in una forza normale. Affinché le forze di tensione superficiale annullino la forza dovuta alla pressione, la superficie deve essere curva. Il diagramma mostra come la curvatura di una piccola zona di superficie porta ad una componente netta delle forze di tensione superficiale che agiscono normalmente al centro della zona. Quando tutte le forze sono bilanciate, l'equazione risultante è nota come equazione di Young-Laplace:
Δ p = γ ( 1 R x + 1 R y ) {displaystyle \Delta p\ = \gamma \sinistra({frac {1}{R_{x}}+{frac {1}{R_{y}}} destra)} 
dove:
· Δp è la differenza di pressione.
· γ {displaystyle \scriptstyle \gamma } è la tensione superficiale.
· Rx e Ry sono i raggi di curvatura in ciascuno degli assi paralleli alla superficie.
La quantità tra parentesi sul lato destro è infatti (due volte) la curvatura media della superficie (a seconda della normalizzazione).
Le soluzioni di questa equazione determinano la forma delle gocce d'acqua, delle pozzanghere, dei menischi, delle bolle di sapone e di tutte le altre forme determinate dalla tensione superficiale. (Un altro esempio è la forma delle impronte che i piedi di uno strider d'acqua fanno sulla superficie di uno stagno).
La tabella qui sotto mostra come la pressione interna di una goccia d'acqua aumenta con il diminuire del raggio. Per gocce non molto piccole l'effetto è sottile, ma la differenza di pressione diventa enorme quando le dimensioni della goccia si avvicinano alla dimensione molecolare. (Nel limite di una singola molecola il concetto diventa privo di significato).
| Δp per gocce d'acqua di diverso raggio a STP | ||||
| Raggio della goccia | 1 mm | 0,1 mm | 1 μm | 10 nm |
| Δp (atm) | 0.0014 | 0.0144 | 1.436 | 143.6 |
Superficie liquida
È difficile trovare la forma della superficie minima delimitata da una cornice di forma arbitraria usando solo la matematica. Eppure, costruendo il telaio con del filo di ferro e immergendolo nella soluzione di sapone, una superficie localmente minima apparirà nella pellicola di sapone risultante in pochi secondi.
La ragione di ciò è che la differenza di pressione attraverso un'interfaccia fluida è proporzionale alla curvatura media, come visto nell'equazione di Young-Laplace. Per un film di sapone aperto, la differenza di pressione è zero, quindi la curvatura media è zero, e le superfici minime hanno la proprietà della curvatura media zero.
Angoli di contatto
La superficie di qualsiasi liquido è un'interfaccia tra quel liquido e qualche altro mezzo. La superficie superiore di uno stagno, per esempio, è un'interfaccia tra l'acqua dello stagno e l'aria. La tensione superficiale, quindi, non è una proprietà del solo liquido, ma una proprietà dell'interfaccia del liquido con un altro mezzo. Se un liquido è in un contenitore, oltre all'interfaccia liquido/aria sulla sua superficie superiore, c'è anche un'interfaccia tra il liquido e le pareti del contenitore. La tensione superficiale tra il liquido e l'aria è solitamente diversa (maggiore) della sua tensione superficiale con le pareti di un contenitore. Dove le due superfici si incontrano, la geometria bilancerà tutte le forze.
Dove le due superfici si incontrano, formano un angolo di contatto, θ {displaystyle \scriptstyle \theta } 
che è l'angolo che la tangente alla superficie fa con la superficie solida. Il diagramma a destra mostra due esempi. Le forze di tensione sono mostrate per l'interfaccia liquido-aria, l'interfaccia liquido-solido e l'interfaccia solido-aria. L'esempio a sinistra è dove la differenza tra la tensione superficiale liquido-solido e solido-aria, γ l s - γ s a {displaystyle \scriptstyle \gamma _{mathrm {ls} \gamma _\mathrm {\mathrm {sa} }} 
è minore della tensione superficiale liquido-aria, γ l a {displaystyle \scriptstyle \gamma _{mathrm {la} }} 
ma è ancora positiva, cioè
γ l a > γ l s - γ s a > 0 {displaystyle \gamma _{mathrm {la} \gamma _\mathrm {\mathrm {ls} \gamma _\mathrm {\mathrm}- \mathrm {sa} }\ >\ 0} 
Nel diagramma, sia la forza verticale che quella orizzontale devono annullarsi esattamente nel punto di contatto, noto come equilibrio. La componente orizzontale di f l a {displaystyle \scriptstyle f_{mathrm {la} 
è annullata dalla forza adesiva, f A {displaystyle \scriptstyle f_{mathrm {A} }} 
.
f A = f l a sin θ {displaystyle f_{mathrm {A} == f_{mathrm {la} sin \theta } 
L'equilibrio di forze più importante, però, è nella direzione verticale. La componente verticale di f l a {displaystyle \scriptstyle f_{mathrm {la} deve esattamente annullare la forza, f l s {displaystyle \scriptstyle f_{mathrm {ls} }} 
.
f l s - f s a = - f l a cos θ {displaystyle f_{mathrm {ls} f_{mathrm {sa} == -f_{mathrm {la} {\an8}Cos'è il cos'è il cos'è il cos'è il cos'è il cos'è il cos'è} 
| Liquido | Solido | Angolo di contatto | |||
| 0° | ||||
| etere dietilico | |||||
| tetracloruro di carbonio | |||||
| glicerolo | |||||
| acido acetico | |||||
| cera di paraffina | 107° | ||||
| argento | 90° | ||||
| ioduro di metile | vetro soda-lime | 29° | |||
| vetro al piombo | 30° | ||||
| quarzo fuso | 33° | ||||
| vetro soda-lime | 140° | ||||
| Alcuni angoli di contatto liquido-solido | |||||
Poiché le forze sono direttamente proporzionali alle rispettive tensioni superficiali, abbiamo anche:
γ l s - γ s a = - γ l a cos θ {displaystyle \gamma _{mathrm {ls} \gamma _\mathrm {\mathrm}- \gamma {\mathrm {\mathrm {\mathrm} == -\gamma _{mathrm {\mathrm {la} \cos \theta } 
dove
· γ l s {displaystyle \scriptstyle \gamma _{mathrm {ls} 
è la tensione superficiale liquido-solido,
· γ l a {displaystyle \scriptstyle \gamma _{mathrm {la} è la tensione superficiale liquido-aria,
· γ s a {displaystyle \scriptstyle \gamma _{mathrm {sa} 
è la tensione superficiale solido-aria,
· θ {displaystyle \scriptstyle \theta } è l'angolo di contatto, dove un menisco concavo ha un angolo di contatto inferiore a 90° e un menisco convesso ha un angolo di contatto superiore a 90°.
Questo significa che anche se la differenza tra la tensione superficiale liquido-solido e solido-aria, γ l s - γ s a {displaystyle \scriptstyle \gamma _{mathrm {ls} \gamma _\mathrm {\mathrm {sa} }} è difficile da misurare direttamente, può essere dedotta dalla tensione superficiale liquido-aria, γ l a {displaystyle \scriptstyle \gamma _{mathrm {la} }} , e l'angolo di contatto di equilibrio, θ {displaystyle \scriptstyle \theta } che è una funzione degli angoli di contatto che avanzano e si allontanano, facilmente misurabili (vedi articolo principale angolo di contatto).
Questa stessa relazione esiste nel diagramma a destra. Ma in questo caso vediamo che poiché l'angolo di contatto è inferiore a 90°, la differenza di tensione superficiale liquido-solido/solido-aria deve essere negativa:
γ l a > 0 > γ l s - γ s a {displaystyle \gamma _{mathrm {la} 0 > 0 > \gamma _\mathrm {\mathrm {\mathrm {ls} \gamma _\mathrm {\mathrm {sa} }} 
Angoli di contatto speciali
Si osservi che nel caso speciale di un'interfaccia acqua-argento dove l'angolo di contatto è uguale a 90°, la differenza di tensione superficiale liquido-solido/solido-aria è esattamente zero.
Un altro caso speciale è quello in cui l'angolo di contatto è esattamente 180°. L'acqua con Teflon appositamente preparato si avvicina a questo valore. L'angolo di contatto di 180° si verifica quando la tensione superficiale liquido-solido è esattamente uguale alla tensione superficiale liquido-aria.
γ l a = γ l s - γ s a > 0 θ = 180 ∘ {displaystyle \gamma _{mathrm {la} = \gamma _{mathrm {s} \gamma _\mathrm {\mathrm {sa} 0\qquadro \theta \= 180^{\circuito} 
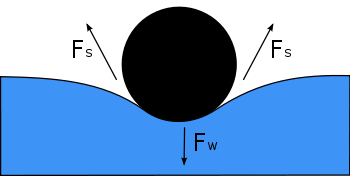
Il diagramma mostra, in sezione trasversale, un ago che galleggia sulla superficie dell'acqua. Il suo peso, Fw, deprime la superficie ed è bilanciato dalle forze di tensione superficiale su entrambi i lati, Fs, che sono ciascuna parallela alla superficie dell'acqua nei punti di contatto con l'ago. Notate che le componenti orizzontali delle due frecce Fs puntano in direzioni opposte, quindi si annullano a vicenda, ma le componenti verticali puntano nella stessa direzione e quindi si sommano per bilanciare Fw.
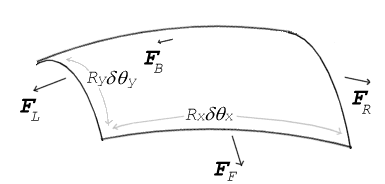
Forze di tensione superficiale che agiscono su una piccola chiazza (differenziale) di superficie. δθx e δθy indicano l'entità della flessione sulle dimensioni della chiazza. Bilanciare le forze di tensione con la pressione porta all'equazione di Young-Laplace
Superficie minima
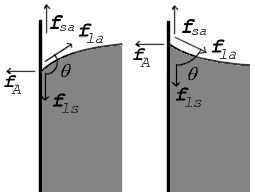
Forze sul punto di contatto mostrate per un angolo di contatto maggiore di 90° (sinistra) e minore di 90° (destra)
Metodi di misurazione
Poiché la tensione superficiale si manifesta in vari effetti, offre un certo numero di percorsi per la sua misurazione. Il metodo ottimale dipende dalla natura del liquido da misurare, dalle condizioni in cui la sua tensione deve essere misurata e dalla stabilità della sua superficie quando viene deformata.
- Metodo Du Noüy Ring: Il metodo tradizionale usato per misurare la tensione superficiale o interfacciale. Le proprietà di bagnatura della superficie o dell'interfaccia hanno poca influenza su questa tecnica di misurazione. Si misura la forza massima esercitata sull'anello dalla superficie.
- Metodo Du Noüy-Padday: Una versione minimizzata del metodo Du Noüy utilizza un ago metallico di piccolo diametro al posto di un anello, in combinazione con una microbilancia ad alta sensibilità per registrare la massima forza di trazione. Il vantaggio di questo metodo è che volumi di campione molto piccoli (fino a poche decine di microlitri) possono essere misurati con una precisione molto alta, senza la necessità di correggere la galleggiabilità (per un ago o piuttosto un'asta, con una geometria adeguata). Inoltre, la misurazione può essere eseguita molto rapidamente, minimamente in circa 20 secondi. I primi tensiometri commerciali multicanale [CMCeeker] sono stati recentemente costruiti sulla base di questo principio.
- Metodo della piastra di Wilhelmy: Un metodo universale particolarmente adatto per controllare la tensione superficiale su lunghi intervalli di tempo. Un piatto verticale di perimetro noto è attaccato a una bilancia, e la forza dovuta alla bagnatura viene misurata.
- Metodo della goccia rotante: Questa tecnica è ideale per misurare basse tensioni interfacciali. Il diametro di una goccia all'interno di una fase pesante viene misurato mentre entrambe vengono ruotate.
- Metodo della goccia pendente: La tensione superficiale e interfacciale può essere misurata con questa tecnica, anche a temperature e pressioni elevate. La geometria di una goccia viene analizzata otticamente. Per i dettagli, vedi Goccia.
- Metodo della pressione delle bolle (metodo di Jaeger): Una tecnica di misurazione per determinare la tensione superficiale a brevi intervalli di tempo. Si misura la pressione massima di ogni bolla.
- Metodo del volume delle gocce: Un metodo per determinare la tensione interfacciale in funzione dell'età dell'interfaccia. Un liquido di una densità viene pompato in un secondo liquido di densità diversa e si misura il tempo tra le gocce prodotte.
- Metodo di risalita capillare: L'estremità di un capillare è immersa nella soluzione. L'altezza a cui la soluzione arriva all'interno del capillare è legata alla tensione superficiale dall'equazione discussa qui sotto.
- Metodo stalagmometrico: Un metodo per pesare e leggere una goccia di liquido.
- Metodo della goccia sessile: Un metodo per determinare la tensione superficiale e la densità mettendo una goccia su un substrato e misurando l'angolo di contatto (vedi tecnica della goccia sessile).
- Frequenza vibrazionale di gocce levitate: La tensione superficiale del superfluido 4He è stata misurata studiando la frequenza naturale delle oscillazioni vibrazionali delle gocce tenute in aria dalla magnetica. Questo valore è stimato essere 0,375 dyn/cm a T = 0° K.
La tensione superficiale può essere misurata con il metodo della goccia pendente su un goniometro.
Effetti
Liquido in un tubo verticale
Un barometro a mercurio vecchio stile consiste in un tubo di vetro verticale di circa 1 cm di diametro parzialmente riempito di mercurio, e con un vuoto (chiamato vuoto di Torricelli) nel volume non riempito (vedi schema a destra). Si noti che il livello di mercurio al centro del tubo è più alto che ai bordi, rendendo la superficie superiore del mercurio a forma di cupola. Il centro di massa dell'intera colonna di mercurio sarebbe leggermente più basso se la superficie superiore del mercurio fosse piatta su tutta la sezione del tubo. Ma la parte superiore a forma di cupola dà una superficie leggermente inferiore all'intera massa di mercurio. Ancora una volta i due effetti si combinano per minimizzare l'energia potenziale totale. Una tale forma di superficie è nota come menisco convesso.
Consideriamo la superficie dell'intera massa di mercurio, compresa la parte della superficie che è in contatto con il vetro, perché il mercurio non aderisce affatto al vetro. Quindi la tensione superficiale del mercurio agisce su tutta la sua superficie, compresa la parte in contatto con il vetro. Se invece del vetro, il tubo fosse fatto di rame, la situazione sarebbe molto diversa. Il mercurio aderisce aggressivamente al rame. Quindi, in un tubo di rame, il livello di mercurio al centro del tubo sarà più basso che ai bordi (cioè, sarebbe un menisco concavo). In una situazione in cui il liquido aderisce alle pareti del suo contenitore, consideriamo che la parte della superficie del fluido che è in contatto con il contenitore ha una tensione superficiale negativa. Il fluido lavora quindi per massimizzare l'area della superficie di contatto. Quindi in questo caso, aumentando l'area a contatto con il contenitore, l'energia potenziale diminuisce invece di aumentare. Questa diminuzione è sufficiente a compensare l'aumento dell'energia potenziale associata al sollevamento del fluido vicino alle pareti del contenitore.
Se un tubo è sufficientemente stretto e l'adesione del liquido alle sue pareti è sufficientemente forte, la tensione superficiale può attirare il liquido su per il tubo in un fenomeno noto come azione capillare. L'altezza a cui la colonna viene sollevata è data da:
h = 2 γ l a cos θ ρ g r {displaystyle h\ = {\frac {2\gamma _{mathrm {la} {\code(0144)\cos \theta {\code(0144)\rho gr}} 
dove
· h {displaystyle \scriptstyle h}
è l'altezza con cui il liquido viene sollevato,
· γ l a {displaystyle \scriptstyle \gamma _{mathrm {la} è la tensione superficiale liquido-aria,
· ρ {displaystyle \scriptstyle \rho }
è la densità del liquido,
· r {displaystyle \scriptstyle r}
è il raggio del capillare,
· g {displaystyle \scriptstyle g}
è l'accelerazione dovuta alla gravità,
· θ {displaystyle \scriptstyle \theta } è l'angolo di contatto descritto sopra. Se θ {displaystyle \scriptstyle \theta } è maggiore di 90°, come con il mercurio in un contenitore di vetro, il liquido sarà depresso piuttosto che sollevato.
Pozzanghere su una superficie
Versando il mercurio su una lastra di vetro piatta orizzontale si ottiene una pozza che ha uno spessore percepibile. La pozza si diffonderà solo fino al punto in cui è un po' meno di mezzo centimetro di spessore, e non più sottile. Anche questo è dovuto all'azione della forte tensione superficiale del mercurio. La massa liquida si appiattisce perché questo porta la maggior parte del mercurio al livello più basso possibile, ma la tensione superficiale, allo stesso tempo, agisce per ridurre la superficie totale. Il risultato è il compromesso di una pozza di uno spessore quasi fisso.
La stessa dimostrazione della tensione superficiale può essere fatta con acqua, acqua di calce o anche salina, ma solo se il liquido non aderisce al materiale della superficie piatta. La cera è una tale sostanza. L'acqua versata su una superficie di cera liscia, piatta e orizzontale, diciamo un foglio di vetro cerato, si comporterà in modo simile al mercurio versato sul vetro.
Lo spessore di una pozza di liquido su una superficie il cui angolo di contatto è 180° è dato da:
h = 2 γ g ρ {displaystyle h\ = 2{sqrt {frac {gamma }grho }}}} 
dove
| h {\displaystyle \scriptstyle h} |
| γ {displaystyle \scriptstyle \gamma } |
| g {displaystyle \scriptstyle g} |
| ρ {displaystyle \scriptstyle \rho } |
In realtà, lo spessore delle pozzanghere sarà leggermente inferiore a quello previsto dalla formula di cui sopra perché pochissime superfici hanno un angolo di contatto di 180° con qualsiasi liquido. Quando l'angolo di contatto è inferiore a 180°, lo spessore è dato da:
h = 2 γ l a ( 1 - cos θ ) g ρ . h\sqrt {2\frac {2\gamma _{mathrm {la} a sinistra (1-cos \theta \destra){g\rho}. } 
Per il mercurio su vetro, γHg = 487 dyn/cm, ρHg = 13,5 g/cm3 e θ = 140°, che dà hHg = 0,36 cm. Per l'acqua su paraffina a 25 °C, γ = 72 dyn/cm, ρ = 1,0 g/cm3, e θ = 107° che dà hH2O = 0,44 cm.
La formula prevede anche che quando l'angolo di contatto è di 0°, il liquido si diffonderà in uno strato micro-sottile sulla superficie. Una tale superficie è detta completamente bagnabile dal liquido.
La rottura dei flussi in gocce
Nella vita quotidiana tutti noi osserviamo che un getto d'acqua che esce da un rubinetto si romperà in goccioline, non importa quanto dolcemente il flusso venga emesso dal rubinetto. Questo è dovuto a un fenomeno chiamato instabilità di Plateau-Rayleigh, che è interamente una conseguenza degli effetti della tensione superficiale.
La spiegazione di questa instabilità inizia con l'esistenza di piccole perturbazioni nel flusso. Queste sono sempre presenti, non importa quanto sia liscio il flusso. Se le perturbazioni sono risolte in componenti sinusoidali, troviamo che alcune componenti crescono con il tempo mentre altre decadono con il tempo. Tra quelle che crescono con il tempo, alcune crescono più velocemente di altre. Se una componente decade o cresce, e quanto velocemente cresce è interamente una funzione del suo numero d'onda (una misura di quanti picchi e depressioni per centimetro) e dei raggi del flusso cilindrico originale.
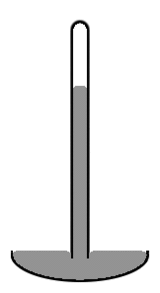
Diagramma di un barometro a mercurio
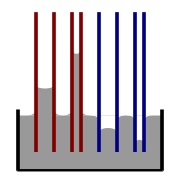
Illustrazione della salita e della discesa capillare. Rosso=angolo di contatto inferiore a 90°; blu=angolo di contatto superiore a 90
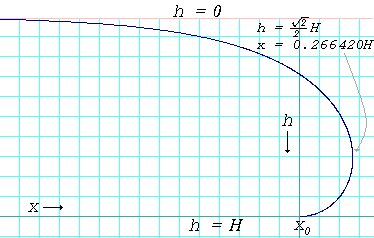
Curva di profilo del bordo di una pozzanghera dove l'angolo di contatto è di 180°. La curva è data dalla formula x - x 0 = 1 2 H cosh - 1 ( H h ) - H 1 - h 2 H 2 {\displaystyle \scriptstyle x-x_{0}\ = {\frac {1}{2}}H\cosh ^{-1}} a sinistra({\frac {H}{h}} a destra)-H{sqrt {1-{frac {h^{2}}{H^{2}}}}}} 
dove H = 2 γ g ρ {\displaystyle \scriptstyle H\= 2{sqrt {frac {gamma }{g\rho }}}} 
Piccole pozze d'acqua su una superficie liscia e pulita hanno uno spessore percepibile.
Illustrazione di come un angolo di contatto più basso porta alla riduzione della profondità della pozzanghera
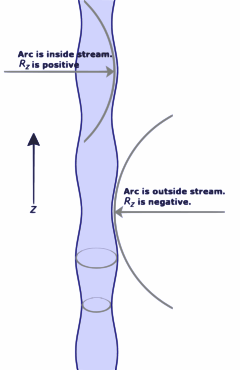
Fase intermedia di un getto che si rompe in gocce. Sono mostrati i raggi di curvatura nella direzione assiale. L'equazione per il raggio della corrente è R ( z ) = R 0 + A k cos ( k z ) {displaystyle \scriptstyle R\left(z\right)=R_{0}+A_{k}cos \left(kz\right)} 
dove R 0 {displaystyle \scriptstyle R_{0}}
è il raggio della corrente imperturbata, A k {displaystyle \scriptstyle A_{k}}
è l'ampiezza della perturbazione, z {displaystyle \scriptstyle z}
è la distanza lungo l'asse della corrente, e k {displaystyle \scriptstyle k}
è il numero di onda
Tabella dei dati
| Tensione superficiale di vari liquidi in dyn/cm contro l'ariaLe | ||
| Liquido | Temperatura °C | Tensione superficiale, γ |
| Acido acetico | 20 | 27.6 |
| Acido acetico (40,1%) + Acqua | 30 | 40.68 |
| Acido acetico (10,0%) + Acqua | 30 | 54.56 |
| Acetone | 20 | 23.7 |
| Etere dietilico | 20 | 17.0 |
| Etanolo | 20 | 22.27 |
| Etanolo (40%) + Acqua | 25 | 29.63 |
| Etanolo (11,1%) + Acqua | 25 | 46.03 |
| Glicerolo | 20 | 63 |
| n-Esano | 20 | 18.4 |
| Acido cloridrico 17,7M soluzione acquosa | 20 | 65.95 |
| Isopropanolo | 20 | 21.7 |
| Azoto liquido | -196 | 8.85 |
| 15 | 487 | |
| Metanolo | 20 | 22.6 |
| n-Octane | 20 | 21.8 |
| Soluzione acquosa di cloruro di sodio 6.0M | 20 | 82.55 |
| Saccarosio (55%) + acqua | 20 | 76.45 |
| Acqua | 0 | 75.64 |
| Acqua | 25 | 71.97 |
| Acqua | 50 | 67.91 |
| Acqua | 100 | 58.85 |
Galleria di effetti
· 
Rottura di uno strato d'acqua in movimento che rimbalza su un cucchiaio.
· 
Foto di acqua corrente che aderisce a una mano. La tensione superficiale crea il foglio d'acqua tra il flusso e la mano.
· 
Una bolla di sapone bilancia le forze di tensione superficiale contro la pressione pneumatica interna.
· 
La tensione superficiale impedisce a una moneta di affondare: la moneta è indiscutibilmente più densa dell'acqua, quindi deve spostare un volume maggiore del suo perché la galleggiabilità bilanci la massa.
· 
Una margherita. La totalità del fiore si trova sotto il livello della superficie libera (indisturbata). L'acqua sale dolcemente intorno al suo bordo. La tensione superficiale impedisce all'acqua di riempire l'aria tra i petali ed eventualmente sommergere il fiore.
· 
Una graffetta di metallo galleggia sull'acqua. Di solito può essere aggiunta con cura senza che l'acqua trabocchi.
· .jpg)
Una moneta di alluminio galleggia sulla superficie dell'acqua a 10 °C. Qualsiasi peso extra farebbe cadere la moneta sul fondo.
Domande e risposte
D: Che cos'è la tensione superficiale?
R: La tensione superficiale è un effetto per cui la superficie di un liquido è forte e può sostenere un peso. Fa sì che alcuni piccoli oggetti possano galleggiare sulla superficie, anche se normalmente non potrebbero farlo, e permette ad alcuni insetti (ad esempio gli strigoni d'acqua) di correre sulla superficie dell'acqua.
D: Cosa provoca la tensione superficiale?
R: La tensione superficiale è causata dalle molecole del liquido che sono attratte l'una dall'altra (coesione).
D: Quali sono le dimensioni della tensione superficiale?
R: La tensione superficiale ha la dimensione di forza per unità di lunghezza, o di energia per unità di superficie. Le due dimensioni sono equivalenti, ma quando ci si riferisce all'energia per unità di superficie, si usa il termine energia superficiale, che è un termine più generale nel senso che si applica anche ai solidi e non solo ai liquidi.
D: In che modo la tensione superficiale influisce sulla scienza dei materiali?
R: Nella scienza dei materiali, la tensione superficiale viene utilizzata sia per lo stress superficiale che per l'energia libera superficiale.
D: In che modo la coesione contribuisce alla tensione superficiale?
R: La coesione contribuisce alla tensione superficiale facendo sì che le molecole di un liquido siano attratte l'una dall'altra, il che crea un forte legame sulla sua superficie che può sostenere il peso e permettere a certi oggetti o creature (ad esempio, gli strigoni d'acqua) di interagire con esso in modo diverso da come potrebbero fare altrimenti.
D: In che modo questa proprietà differisce da altre proprietà dei liquidi?
R: Questa proprietà differisce dalle altre proprietà dei liquidi perché influisce sul modo in cui gli oggetti interagiscono con essi sulla loro superficie, piuttosto che al loro interno o attraverso il loro comportamento complessivo.
