Prodotto scalare

In matematica, il prodotto di punti è un'operazione che prende due vettori come input e che restituisce un numero scalare come output. Il numero restituito dipende dalla lunghezza di entrambi i vettori e dall'angolo tra di essi. Il nome deriva dal punto centrato "-" che è spesso usato per designare questa operazione; il nome alternativo prodotto scalare sottolinea la natura scalare (piuttosto che vettoriale) del risultato.

Il prodotto di punti si contrappone (nello spazio tridimensionale) al prodotto incrociato, che produce un vettore come risultato.

Definizione

Il prodotto di punti di due vettori a = [a1, a2, ..., an] e b = [b1, b2, ..., bn] è definito come:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n} {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}

dove Σ denota la notazione di somma (la somma di tutti i termini) e n è la dimensione dello spazio vettoriale.

In una dimensione 2, il prodotto di punto dei vettori [a,b] e [c,d] è ac + bd. Allo stesso modo, in una dimensione 3, il prodotto di punti dei vettori [a,b,c] e [d,e,f] è ad + be + cf. Per esempio, il prodotto di punti di due vettori tridimensionali [1, 3, -5] e [4, -2, -1] è

[ 1 , 3 , − 5 ] ⋅ [ 4 , − 2 , − 1 ] = ( 1 × 4 ) + ( 3 × ( − 2 ) ) + ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1 volta 4)+(3 volte (-2))+((-5)\tempo (-1))=(4)-(6)+(5)=3.} {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.}

Interpretazione geometrica

Nella geometria euclidea, il prodotto del punto, la lunghezza e l'angolo sono correlati. Per un vettore a, il prodotto di punto a - a è il quadrato della lunghezza di a, o

a ⋅ a = ‖ a ‖ 2 {displaystyle {mathbf {a} \cdot \mathbf {a} a destra, a sinistra, a destra, a destra... {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}}

dove ||a|| denota la lunghezza (magnitudine) di a. Più in generale, se b è un altro vettore

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {displaystyle ‖mathbf {a} ‗cdot ‖mathbf {b} = ‗sinistra‖mathbf {a} ‗destra‖,‗sinistra‖mathbf {b} \destra \cos \theta \, \sinistra \mathbf \mathbf \mathbf \mathbf} {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,}

dove ||a|| e ||b|| indicano la lunghezza di a e b e θ è l'angolo tra loro.

Questa formula può essere riorganizzata per determinare la grandezza dell'angolo tra due vettori non nulli:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {displaystyle ‖theta = arccos ‖ a sinistra(‗frac ‗a ‗cdot ‗mathbf ‖ b ‖) ‗a sinistra ‗a destra ‗destra') {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)}

Si può anche convertire prima i vettori in vettori unitari dividendo per la loro magnitudine:

a ^ = a ‖ a ‖ {displaystyle {boldsymbol {hat {a}}={frac {mathbf {a}} a sinistra {mathbf {a} a destra}}} {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}}

allora l'angolo θ è dato da

θ = arccos ( a ^ ⋅ b ^ ) {displaystyle \theta = arccos(a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})}

Poiché il coseno di 90° è zero, il prodotto del punto di due vettori ortogonali (perpendicolari) è sempre zero. Inoltre, due vettori possono essere considerati ortogonali se e solo se il loro prodotto di punto è zero, ed entrambi hanno una lunghezza non nulla. Questa proprietà fornisce un metodo semplice per verificare la condizione di ortogonalità.

A volte queste proprietà sono usate anche per definire il prodotto di punti, specialmente in 2 e 3 dimensioni; questa definizione è equivalente a quella precedente. Per dimensioni superiori la formula può essere usata per definire il concetto di angolo.

Le proprietà geometriche si basano sul fatto che la base sia ortonormale, cioè composta da vettori perpendicolari a coppie di lunghezza unitaria.

Proiezione scalare

Se sia a che b hanno lunghezza uno (cioè, sono vettori unitari), il loro prodotto di punto dà semplicemente il coseno dell'angolo tra loro.

Se solo b è un vettore unitario, allora il prodotto di punto a - b dà |a| cos(θ), cioè la grandezza della proiezione di a nella direzione di b, con un segno meno se la direzione è opposta. Questa è chiamata la proiezione scalare di a su b, o componente scalare di a nella direzione di b (vedi figura). Questa proprietà del prodotto di punti ha diverse applicazioni utili (per esempio, vedi la prossima sezione).

Se né a né b sono vettori unitari, allora la grandezza della proiezione di a nella direzione di b, per esempio, sarebbe a - (b / |b|) poiché il vettore unitario nella direzione di b è b / |b|.

Rotazione

Una rotazione della base ortonormale in termini di cui è rappresentato il vettore a si ottiene con una moltiplicazione di a per una matrice di rotazione R. Questa moltiplicazione di matrice è solo una rappresentazione compatta di una sequenza di prodotti punto.

Per esempio, lasciamo che

  • B1 = {x, y, z} e B2 = {u, v, w} sono due diverse basi ortonormali dello stesso spazio R3, con B2 ottenuta dalla semplice rotazione di B1,
  • a1 = (ax, ay, az) rappresenta il vettore a in termini di B1,
  • a2 = (au, av, aw) rappresentano lo stesso vettore in termini di base ruotata B2,
  • u1, v1, w1 essere i vettori base ruotati u, v, w rappresentati in termini di B1.

Poi la rotazione da B1 a B2 viene eseguita come segue:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}{1}{1}cdot {mathbf {a}{1}{1}{mathbf {w}{1}{mathbf {a}{1} fine{bmatrix}}={begin{bmatrix}a_{u}{a_{v}{a_{w} fine{bmatrix}}. } {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}.}

Si noti che la matrice di rotazione R è assemblata usando i vettori base ruotati u1, v1, w1 come righe, e questi vettori sono vettori unitari. Per definizione, Ra1 consiste in una sequenza di prodotti di punto tra ciascuna delle tre righe di R e il vettore a1. Ognuno di questi prodotti di punto determina una componente scalare di a nella direzione di un vettore base ruotato (vedi sezione precedente).

Se a1 è un vettore riga, piuttosto che un vettore colonna, allora R deve contenere i vettori base ruotati nelle sue colonne, e deve post-moltiplicare a1:

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {mathbf {a}}{2}={mathbf {a}}_{1}{mathbf {R}}={begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}{fine{bmatrix}}={begin{bmatrix}{mathbf {u}}_{1}{cdot {mathbf {a}}_{1}&{mathbf {v}_{1}{mathbf {a}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. } {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.}

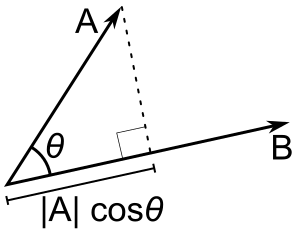
A - B = |A| |B| cos(θ). |A| cos(θ) è la proiezione scalare di A su B.Zoom
A - B = |A| |B| cos(θ). |A| cos(θ) è la proiezione scalare di A su B.

Fisica

In fisica, la grandezza è uno scalare in senso fisico, cioè una quantità fisica indipendente dal sistema di coordinate, espressa come il prodotto di un valore numerico e un'unità fisica, non solo un numero. Anche il prodotto di punti è uno scalare in questo senso, dato dalla formula, indipendente dal sistema di coordinate. Esempio:

Proprietà

Le seguenti proprietà valgono se a, b e c sono vettori reali e r è uno scalare.

Il prodotto di punti è commutativo:

a ⋅ b = b ⋅ a . \cdot \mathbf {a} . } {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} .}

Il prodotto di punti è distributivo sull'addizione vettoriale:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \mathbf {c} \mathbf {c} \mathbf \mathbf \mathbf \mathbf {c} . } {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .}

Il prodotto di punti è bilineare:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). } {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).}

Se moltiplicato per un valore scalare, il prodotto di punti soddisfa:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )} {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )}

(queste ultime due proprietà derivano dalle prime due).

Due vettori a e b non nulli sono perpendicolari se e solo se a - b = 0.

A differenza della moltiplicazione dei numeri ordinari, dove se ab = ac, allora b è sempre uguale a c a meno che a sia zero, il prodotto di punti non obbedisce alla legge di cancellazione:

Se a - b = a - c e a ≠ 0, allora possiamo scrivere: a - (b - c) = 0 per la legge distributiva; il risultato precedente dice che questo significa solo che a è perpendicolare a (b - c), il che permette ancora (b - c) ≠ 0, e quindi b ≠ c.

A condizione che la base sia ortonormale, il prodotto di punti è invariante sotto cambiamenti isometrici della base: rotazioni, riflessioni e combinazioni, mantenendo fissa l'origine. L'interpretazione geometrica di cui sopra si basa su questa proprietà. In altre parole, per uno spazio ortonormale con qualsiasi numero di dimensioni, il prodotto di punti è invariante sotto una trasformazione di coordinate basata su una matrice ortogonale. Questo corrisponde alle due condizioni seguenti:

  • La nuova base è di nuovo ortonormale (cioè, è ortonormale espressa in quella vecchia).
  • I nuovi vettori di base hanno la stessa lunghezza di quelli vecchi (cioè, lunghezza unitaria in termini della vecchia base).

Se a e b sono funzioni, allora la derivata di a - b è a' - b + a - b'

Tripla espansione del prodotto

Questa è un'identità molto utile (conosciuta anche come formula di Lagrange) che coinvolge i prodotti punto e croce. Si scrive come

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )-} {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )}

che è più facile da ricordare come "BAC meno CAB", tenendo presente quali vettori sono punteggiati insieme. Questa formula è comunemente usata per semplificare i calcoli vettoriali in fisica.

Prova dell'interpretazione geometrica

Consideriamo l'elemento di Rn

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . + v n e ^ n . =v_{1}{mathbf {v} =v_{1}{mathbf{hat {e}} {{1}+v_{2}mathbf {e} _{2}+...+v_{n}mathbf {e} _{n}.\,} {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,}

Applicando ripetutamente il teorema di Pitagora si ottiene per la sua lunghezza |v|

| v | 2 = v 1 2 + v 2 2 + . . . + v n 2 . {\displaystyle |mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,} {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

Ma questo è lo stesso che

v ⋅ v = v 1 2 + v 2 2 + . . . + v n 2 , {displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\cit} {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,}

quindi concludiamo che prendendo il prodotto del punto di un vettore v con se stesso si ottiene la lunghezza al quadrato del vettore.

Lemma 1

v ⋅ v = | v | 2 . {\an8}Mathbf {v} \cdot \mathbf {v} =|mathbf {v} |^{2}.\,} {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,}

Consideriamo ora due vettori a e b che si estendono dall'origine, separati da un angolo θ. Un terzo vettore c può essere definito come

c = d e f a - b . {\an8}Mathbf {c} \stackrel \mathrm {\mathrm {def} {\an8}(*). {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,}

creando un triangolo con i lati a, b e c. Secondo la legge dei coseni, abbiamo

| c | 2 = | a | 2 + | b | 2 - 2 | a | | b | cos θ . {\an8}(*Città del mondo.) 2 = a 2 + b 2 + a 2 cos θ. {\an8}+ {mathbf {mathbf {b} 2...2..2...2...2...2...2...2...2...2...2... \mathbf {mathbf {b} \cos \theta .\,} {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Sostituendo i prodotti di punti per le lunghezze quadrate secondo il Lemma 1, otteniamo

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | b | cos θ . {\mathbf {c} \cdot \mathbf {c} =mathbf {a} \cdot \mathbf {a} +mathbf {b} \cdot \mathbf {b} -2|mathbf {a} \mathbf {\mathbf {b} {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}(1)

Ma poiché c ≡ a - b, abbiamo anche

c ⋅ c = ( a - b ) ⋅ ( a - b ) {displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\cdot \{\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,},

che, secondo la legge distributiva, si espande a

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\mathbf {c} \cdot \mathbf {c} =mathbf {a} \cdot \mathbf {a} +mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,}(2)

Unendo le due equazioni c - c, (1) e (2), otteniamo

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | b | cos θ . \displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +mathbf {b} \cdot \mathbf {b} -2|mathbf {a} \mathbf {\mathbf {b} \cos \theta .\,} {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Sottraendo a - a + b - b da entrambi i lati e dividendo per -2 si ottiene

a ⋅ b = | a | b | cos θ . {\an8} \mathbf {a} \cdot \mathbf {b} =|mathbf {a}  \cos \theta .\,} {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Q.E.D.

Generalizzazione

Il prodotto interno generalizza il prodotto punto agli spazi vettoriali astratti ed è solitamente indicato da ⟨ a , b ⟩ {displaystyle ⟩ 【langolo 【mathbf {a},,【mathbf {b} ‗angolo'.} {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle }. Grazie all'interpretazione geometrica del prodotto di punti, la norma di un vettore a in un tale spazio del prodotto interno è definita come

‖ a ‖ = ⟨ a , a ⟩ {displaystyle ‖ = ⟩ ⟩ = ↪Psqrt ‗langolo ‗mathbf {a} ‖,,‗mathbf {a} ‗rangolo ‖} {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}}

tale da generalizzare la lunghezza, e l'angolo θ tra due vettori a e b da

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . {displaystyle \cos \theta }={frac {langolo \mathbf {a},,\mathbf {b} \mathbf \mathbf \mathbf \mathbf \mathbf \mathbf \mathbf \mathbf \mathbf \mathbf \mathbf \|}}. } {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}.}

In particolare, due vettori sono considerati ortogonali se il loro prodotto interno è zero

⟨ a , b ⟩ = 0. 【displaystyle 【langolo 【mathbf {a},,【mathbf {b} ‗angolo' =0.} {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle =0.}

Per i vettori con voci complesse, usare la definizione data del prodotto di punto porterebbe a proprietà geometriche molto diverse. Per esempio, il prodotto di punto di un vettore con se stesso può essere un numero complesso arbitrario, e può essere zero senza che il vettore sia il vettore zero; questo a sua volta avrebbe gravi conseguenze per nozioni come lunghezza e angolo. Molte proprietà geometriche possono essere salvate, al costo di rinunciare alle proprietà simmetriche e bilineari del prodotto scalare, definendo alternativamente

a ⋅ b = ∑ a i b i ¯ {displaystyle \mathbf {a} \cdot \mathbf {b} ==somma {a_{i}{overline {b_{i}}}}} {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}}

dove bi è il coniugato complesso di bi. Allora il prodotto scalare di qualsiasi vettore con se stesso è un numero reale non negativo, ed è non nullo tranne che per il vettore zero. Tuttavia questo prodotto scalare non è lineare in b (ma piuttosto lineare coniugato), e il prodotto scalare non è nemmeno simmetrico, poiché

a ⋅ b = b ⋅ a ¯ {displaystyle \mathbf {a} \cdot \mathbf {b} ={overline {mathbf {b} \cdot \mathbf {mathbf {a} }}} {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}}.

Questo tipo di prodotto scalare è comunque abbastanza utile, e porta alle nozioni di forma hermitiana e di spazi di prodotti interni generali.

Il prodotto interno di Frobenius generalizza il prodotto punto alle matrici. È definito come la somma dei prodotti delle componenti corrispondenti di due matrici che hanno la stessa dimensione.

Generalizzazione ai tensori

Il prodotto di punto tra un tensore di ordine n e un tensore di ordine m è un tensore di ordine n+m-2. Il prodotto di punti si ottiene moltiplicando e sommando un singolo indice in entrambi i tensori. Se A {displaystyle \mathbf {A} {\displaystyle \mathbf {A} }e B {displaystyle \mathbf {B} {\displaystyle \mathbf {B} }sono due tensori con rappresentazione degli elementi A i j ... k ℓ ... {displaystyle A_{ij\punti }^{k\ell \punti }} {\displaystyle A_{ij\dots }^{k\ell \dots }}e B m n ... p ... i {displaystyle B_mn\punti }^{p\punti }i}{\displaystyle B_{mn\dots }^{p{\dots }i}} gli elementi del prodotto di punti A ⋅ B {displaystyle \mathbf {A} \cdot \mathbf {B} {\displaystyle \mathbf {A} \cdot \mathbf {B} }sono dati da

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_ij\dots

Questa definizione si riduce naturalmente al prodotto di punto vettoriale standard quando è applicata ai vettori, e alla moltiplicazione matriciale quando è applicata alle matrici.

Occasionalmente, un doppio prodotto di punti è usato per rappresentare la moltiplicazione e la somma tra due indici. Il doppio prodotto di punti tra due tensori di 2° ordine è uno scalare.

Pagine correlate

 

Domande e risposte

D: Che cos'è il prodotto dei punti in matematica?


R: Il prodotto del punto è un'operazione che prende in ingresso due vettori e restituisce in uscita un numero scalare.

D: Da cosa dipende il prodotto del punto?


R: Il prodotto del punto dipende dalla lunghezza dei due vettori e dall'angolo che li separa.

D: Perché il nome del prodotto del punto deriva dal punto centrato "-"?


R: Il nome deriva dal punto centrato "-" che viene spesso utilizzato per indicare questa operazione.

D: Qual è il nome alternativo del prodotto dei punti?


R: Il nome alternativo è prodotto scalare, che sottolinea la natura scalare (anziché vettoriale) del risultato.

D: Qual è il contrasto tra il prodotto dei punti e il prodotto incrociato nello spazio tridimensionale?


R: Il prodotto dei punti produce un numero scalare come risultato, mentre il prodotto incrociato produce un vettore come risultato.

D: A cosa serve il prodotto dei punti in matematica?


R: Il prodotto dei punti può essere utilizzato per determinare se due vettori sono perpendicolari (hanno un angolo di 90 gradi) e per proiettare un vettore su un altro.

D: Il prodotto del punto può essere utilizzato in spazi di dimensioni superiori?


R: Sì, il prodotto del punto può essere esteso a spazi di dimensioni superiori generalizzando la definizione.

AlegsaOnline.com - 2020 / 2023 - License CC3