Integrale di superficie

In matematica, un integrale di superficie è un integrale definito preso su una superficie (che può essere una curva nello spazio). Proprio come un integrale di linea gestisce una dimensione o una variabile, un integrale di superficie può essere pensato come un doppio integrale lungo due dimensioni. Data una superficie, si può integrare sui suoi campi scalari (cioè le funzioni che restituiscono numeri come valori) e sui campi vettoriali (cioè le funzioni che restituiscono vettori come valori).

Gli integrali di superficie hanno applicazioni in fisica, in particolare nella teoria classica dell'elettromagnetismo.

La definizione di integrale di superficie si basa sulla divisione della superficie in piccoli elementi di superficie.

Un'illustrazione di un singolo elemento di superficie. Questi elementi sono resi infinitesimamente piccoli, dal processo di limitazione, in modo da approssimare la superficie.

Integrali di superficie di campi scalari

Consideriamo una superficie S su cui è definito un campo scalare f. Se si pensa a S come fatto di qualche materiale, e per ogni x in S il numero f(x) è la densità del materiale in x, allora l'integrale di superficie di f su S è la massa per unità di spessore di S. (Questo è vero solo se la superficie è un guscio infinitesimamente sottile.Un approccio al calcolo dell'integrale di superficie è quindi dividere la superficie in molti pezzi molto piccoli, assumere che su ogni pezzo la densità sia approssimativamente costante, trovare la massa per unità di spessore di ogni pezzo moltiplicando la densità del pezzo per la sua area, e poi sommare i numeri risultanti per trovare la massa totale per unità di spessore di S.

Per trovare una formula esplicita per l'integrale di superficie, i matematici parametrizzano S considerando su S un sistema di coordinate curvilinee, come la latitudine e la longitudine su una sfera. Sia tale parametrizzazione x(s, t), dove (s, t) varia in qualche regione T nel piano. Allora, l'integrale di superficie è dato da

∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | d s d t {displaystyle \int _{S}f\,dS= \iint _{T}f(\mathbf {x} (s,t))\sinistra|parziale di \mathbf {x} su \partial s\mathbf (s,t) su \parziale t}destra \ds,dt} $\int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right|ds\,dt$

dove l'espressione tra le barre sul lato destro è la grandezza del prodotto incrociato delle derivate parziali di x(s, t).

Per esempio, per trovare la superficie di una qualche forma funzionale generale, diciamo z = f ( x , y ) {\displaystyle z=f\,(x,y)} $z=f\,(x,y)$ , abbiamo

A = ∫ S d S = ∬ T ∂ r ∂ r ∂ x × ∂ r ∂ y ∂ d x d y {displaystyle A = ∫int _{S},dS= ∫iint _{T} ∂ a sinistra su \partial x}, volte \mathbf \mathbf \mathbf \mathbf \mathbf \mathbf \mathbf \mathbf su \pari a y}destra,dy} e su \dx,dy} $A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \over \partial x}\times {\partial \mathbf {r} \over \partial y}\right\|dx\,dy$

dove r = ( x , y , z ) = ( x , y , f ( x , y ) ) {\displaystyle \mathbf {r} =(x,y,z)=(x,y,f(x,y))} $\mathbf {r} =(x,y,z)=(x,y,f(x,y))$ . Così che ∂ r ∂ x = ( 1 , 0 , f x ( x , y ) ) {displaystyle {parziale \mathbf {r} su \parziale x}=(1,0,f_{x}(x,y))} ${\partial \mathbf {r} \over \partial x}=(1,0,f_{x}(x,y))$ , e ∂ r ∂ y = ( 0 , 1 , f y ( x , y ) ) , e ∂ r ∂ y = ( 0 , 1 , f y ( x , y ) ) su \parziale y}=(0,1,f_{y}(x,y))} ${\partial \mathbf {r} \over \partial y}=(0,1,f_{y}(x,y))$ . Quindi,

A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\displaystyle {\begin{aligned}A&{ {}=iint _{T}{sinistra}{sinistra(1,0,{parziale f su \parziale x}destra)\tempi \sinistra(0,1,{parziale f su \parziale y}destra)\destra|dx\x,dy\x{ {\an8}Si prega di non utilizzare i tasti "destra" o "destra" per il calcolo del numero di cifre che si desidera ottenere.{}=iint _{T}{sqrt {sinistra(f parziale su x parziale) a destra)^{2}+sinistra(f parziale su y parziale) a destra)^{2}+1}},\x,dx,dy{aligned}}} ${\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\|\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\right\|dx\,dy\\&{}=\iint _{T}{\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}\,\,dx\,dy\end{aligned}}$

che è la formula usata per la superficie di una forma funzionale generale. Si può riconoscere il vettore nella seconda riga sopra come il vettore normale alla superficie.

Si noti che a causa della presenza del prodotto incrociato, le formule di cui sopra funzionano solo per le superfici incorporate nello spazio tridimensionale.

Integrali di superficie di campi vettoriali

Consideriamo un campo vettoriale v su S, cioè, per ogni x in S, v(x) è un vettore.

L'integrale di superficie può essere definito per componenti secondo la definizione dell'integrale di superficie di un campo scalare; il risultato è un vettore. Per esempio, questo si applica al campo elettrico in un punto fisso dovuto a una superficie elettricamente carica, o alla gravità in un punto fisso dovuto a un foglio di materiale. Può anche calcolare il flusso magnetico attraverso una superficie.

In alternativa, i matematici possono integrare la componente normale del campo vettoriale; il risultato è uno scalare. Un esempio è un fluido che scorre attraverso S, così che v(x) determina la velocità del fluido a x. Il flusso è definito come la quantità di fluido che scorre attraverso S in una quantità unitaria di tempo.

Questa illustrazione implica che se il campo vettoriale è tangente a S in ogni punto, allora il flusso è zero, perché il fluido scorre solo parallelamente a S, e né dentro né fuori. Questo implica anche che se v non scorre solo lungo S, cioè se v ha sia una componente tangenziale che una normale, allora solo la componente normale contribuisce al flusso. Sulla base di questo ragionamento, per trovare il flusso, dobbiamo prendere il prodotto di punto di v con l'unità di superficie normale a S in ogni punto, che ci darà un campo scalare, e integrare il campo ottenuto come sopra. Questo dà la formula

∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t . Se si tratta di un'azione che non ha nulla a che vedere con la realtà, il problema è che non si tratta di un'azione che non ha nulla a che vedere con la realtà, ma di un'azione che non ha nulla a che vedere con la realtà. \int _{S}({mathbf {v}}cdot {mathbf {n})\,dS=iint _{T}{mathbf {v}(\mathbf {v}(\mathbf {x} (s,t))\cdot \sinistra(\parziale \mathbf {x} su \partial s\mathbf\mathbf\mathbf\mathbf\mathbf\mathbf\mathbf\mathbf\mathbf\mathbf_italian su \parziale t}destra)ds,dt. } $\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right)ds\,dt.$

Il prodotto incrociato sul lato destro di questa espressione è una normale alla superficie determinata dalla parametrizzazione.

Questa formula definisce l'integrale a sinistra (notare il punto e la notazione vettoriale per l'elemento di superficie).

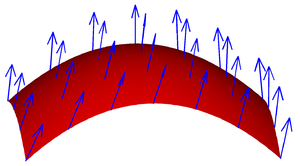
Un campo vettoriale su una superficie.

Teoremi sugli integrali di superficie

Vari risultati utili per gli integrali di superficie possono essere derivati usando la geometria differenziale e il calcolo vettoriale, come il teorema di divergenza e la sua generalizzazione, il teorema di Stokes.

Problemi avanzati

Modifica della parametrizzazione

La discussione precedente ha definito l'integrale di superficie usando una parametrizzazione della superficie S. Una data superficie potrebbe avere diverse parametrizzazioni. Per esempio, quando le posizioni del Polo Nord e del Polo Sud vengono spostate su una sfera, la latitudine e la longitudine cambiano per tutti i punti della sfera. Una domanda naturale è quindi se la definizione dell'integrale di superficie dipende dalla parametrizzazione scelta. Per gli integrali di campi scalari, la risposta a questa domanda è semplice, il valore dell'integrale di superficie sarà lo stesso indipendentemente dalla parametrizzazione che si usa.

Gli integrali di campi vettoriali sono più complicati, perché è coinvolta la normale alla superficie. I matematici hanno dimostrato che date due parametrizzazioni della stessa superficie, le cui normali di superficie puntano nella stessa direzione, entrambe le parametrizzazioni danno lo stesso valore per l'integrale di superficie. Se, invece, le normali di queste parametrizzazioni puntano in direzioni opposte, il valore dell'integrale di superficie ottenuto usando una parametrizzazione è il negativo di quello ottenuto tramite l'altra parametrizzazione. Ne consegue che, data una superficie, non è necessario attenersi a una parametrizzazione unica; ma, quando si integrano campi vettoriali, è necessario decidere in anticipo in quale direzione punterà la normale e quindi scegliere qualsiasi parametrizzazione coerente con quella direzione.

Le parametrizzazioni lavorano su parti della superficie

Un altro problema è che a volte le superfici non hanno parametrizzazioni che coprono l'intera superficie; questo è vero per esempio per la superficie di un cilindro (di altezza finita). La soluzione ovvia è allora dividere quella superficie in diversi pezzi, calcolare l'integrale di superficie su ogni pezzo e poi sommarli tutti. Questo è effettivamente il modo in cui funzionano le cose, ma quando si integrano campi vettoriali bisogna ancora una volta fare attenzione a come scegliere il vettore di puntamento normale per ogni pezzo della superficie, in modo che quando i pezzi vengono rimessi insieme, i risultati siano coerenti. Per il cilindro, questo significa che se decidiamo che per la regione laterale la normale punterà fuori dal corpo, allora anche per le parti circolari superiore e inferiore la normale deve puntare fuori dal corpo.

Normali di superficie incoerenti

Infine, ci sono superfici che non hanno una normale di superficie in ogni punto con risultati coerenti (per esempio, il nastro di Möbius). Se una tale superficie viene divisa in pezzi, su ogni pezzo viene scelta una parametrizzazione e la corrispondente normale alla superficie, e i pezzi vengono rimessi insieme, i vettori normali provenienti da pezzi diversi non possono essere conciliati. Questo significa che in qualche giunzione tra due pezzi avrà vettori normali che puntano in direzioni opposte. Una tale superficie è chiamata non orientabile. I campi vettoriali non possono essere integrati su superfici non orientabili.

Pagine correlate

Teorema della divergenza
Teorema di Stokes
Integrale di linea
Integrale del volume
Sistema di coordinate cartesiane
Elementi di volume e superficie in un sistema di coordinate sferiche
Elementi di volume e superficie in un sistema di coordinate cilindriche
Metodo Holstein-Herring