Serie armonica

In matematica, la serie armonica è la serie infinita divergente:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\a6}}}{\a6}{\a6}}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6} $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Divergente significa che, aggiungendo altri termini, la somma non smette mai di crescere. Non va verso un singolo valore finito.

Infinito significa che si può sempre aggiungere un altro termine. Non c'è un termine finale alla serie.

Il suo nome deriva dall'idea degli armonici nella musica: le lunghezze d'onda dei toni di una corda vibrante sono 1/2, 1/3, 1/4, ecc. della lunghezza d'onda fondamentale della corda. A parte il primo termine, ogni termine della serie è la media armonica dei termini da una parte e dall'altra. La media armonica della frase deriva anche dalla musica.

Storia

Il fatto che la serie armonica diverga è stato dimostrato per la prima volta nel XIV secolo da Nicole Oresme, ma è stato dimenticato. Le prove furono fornite nel XVII secolo da Pietro Mengoli, Johann Bernoulli e Jacob Bernoulli.

Le sequenze armoniche sono state utilizzate dagli architetti. Nel periodo barocco gli architetti le utilizzavano nelle proporzioni delle piante, nei prospetti e nelle relazioni tra i dettagli architettonici di chiese e palazzi.

Divergenza

Ci sono diverse prove ben note della divergenza delle serie armoniche. Alcune di esse sono riportate di seguito.

Test di confronto

Un modo per dimostrare la divergenza è quello di confrontare le serie armoniche con un'altra serie divergente, dove ogni denominatore viene sostituito con la potenza di due successivi:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\a6}&{}1+{{{{frac {1}{2}}+{{{frac {1}{3}}+{{{frac {1}{4}}+{{frac {1}{5}}+{{frac {1}{6}}+{{frac {1}{7}}+{{frac {1}{8}}+{{{frac {1}{9}+++cdots \fscx130\fscy130\frx40}&1+{\frac {\an8}{\an8}+{\an8}+frac {\an8}{\an8} # -frac # # - colore rosso # # -mathbf # # - colore rosso # # -mathbf # # colore rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso. # colore rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso, rosso. # -frac... # # -frac... # # -frac... # # -frac... # i punti si sono allineati. ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

Ogni termine della serie armonica è maggiore o uguale al termine corrispondente della seconda serie, e quindi la somma delle serie armoniche deve essere maggiore o uguale alla somma della seconda serie. Tuttavia, la somma della seconda serie è infinita:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\fscx130\fscy130\fscy130\frx40}&{\fscx130\fscy130\frx40}&{\fscy130\frx40}1+sinistra(frac {1}{2}{\fscx130\fscy130\frx40}}}Destra)+sinistra(frac {\fscx130\fscy130\frx40}{\fscy130\frx40}}{\fscy130\frx40}}Sinistra!+\Destra, sinistra, sinistra!+\Destra!Frac 1x16 + punti =&1++frac 1x2++frac 1x2++frac 1x2++frac 1x2++frac 1x2+frac 1x2++frac 1x2+frac 1x2++frac 1x2+frac 1x2+frac 1x2+frac 1x2+frac 2x2 ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

Ne consegue (dalla prova di confronto) che anche la somma delle serie armoniche deve essere infinita. Più precisamente, il confronto di cui sopra dimostra che

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\a6}}{n=1}^{2^{k}}{\a6}}}{1}{n}}}geq 1+{\a6}}frac {k}{2}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

per ogni numero intero positivo $k$ .

Questa prova, proposta da Nicole Oresme intorno al 1350, è considerata un punto culminante della matematica medievale. È ancora oggi una prova standard insegnata nelle classi di matematica.

Test integrale

È possibile dimostrare che la serie armonica diverge confrontando la sua somma con un integrale non corretto. Si consideri la disposizione dei rettangoli mostrata nella figura a destra. Ogni rettangolo è largo 1 unità e alto 1/n unità, quindi l'area totale del numero infinito di rettangoli è la somma delle serie armoniche:

area dei rettangoli = 1 + 1 2 + 1 3 + 1 3 + 1 4 + 1 5 + ⋯ ${\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

L'area totale sotto la curva $y =$ 1/x da 1 a infinito è data da un integrale improprio divergente:

area sotto la curva = ∫ 1 ∞ 1 x d x = ∞ . displaystyle inizia con l'area sotto la curva del testo sotto l'area sotto la curva del testo. } ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

Poiché quest'area è interamente contenuta all'interno dei rettangoli, anche l'area totale dei rettangoli deve essere infinita. Questo dimostra che

∑ n = 1 k 1 n > ∫ 1 k + 1 1 1 x d x = ln ( k + 1 ) . {\an8}{n=1}^{k}{{frac {1}{n}}>int _{1}^{k+1}{frac {1}{x}},dx=\an8}ln(k+1). } $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

La generalizzazione di questo argomento è nota come test integrale.

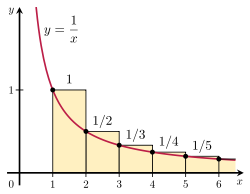
Illustrazione del test integrale.

Tasso di divergenza

La serie armonica diverge molto lentamente. Ad esempio, la somma dei primi ¹⁰⁴³ termini è inferiore a 100. Questo perché le somme parziali delle serie hanno una crescita logaritmica. In particolare,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\an8}{n=1}^{k}{\an8}}{\an8}frac {1}{n}=\an8}ln k+\an8}gamma +varepsilon _{k}leq (\ln k)+1} $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

dove γ è la costante di Eulero-Mascheroni e εk $~$ 1/2k che si avvicina a 0 come $k$ va all'infinito. Leonhard Euler ha dimostrato sia questo che che che la somma che include solo i reciproci dei primati diverge, cioè:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . . } $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

Somme parziali

I primi trenta numeri armonici
$n$	Somma parziale della serie armonica, $Hn$
$n$	espresso come frazione		decimale	dimensione relativa
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Le somme parziali finite delle serie armoniche divergenti,

H n = ∑ k = 1 n 1 k , {\a6}}}[H_{n}=sum _{k=1}^{n}{n}{frac {1}{k},} $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

sono chiamati numeri armonici.

La differenza tra $Hn$ e $ln n$ converge alla costante Euler-Mascheroni. La differenza tra due numeri armonici qualsiasi non è mai un numero intero. Nessun numero armonico è un numero intero, ad eccezione di $H1 = 1$ .

Serie correlate

Serie armoniche alternate

La serie

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\a6}{\a6}}{\a6}}{\a6}}}=1-{\a6}{\a6}+{\a6}}+{\a6}{\a6}}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6}{\a6} $\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots$

è nota come serie armonica alternata. Questa serie converge con la prova della serie alternata. In particolare, la somma è pari al logaritmo naturale di 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. 1-{\frac {1}{2}}+{\frac {1}{\an8}}+{\an8}frac {\an8}{\an8}frac {1}{\an8}+{\an8}frac {\an8}{\an8}frac {\an8}{\an8} $1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$

La serie armonica alternata, pur essendo condizionatamente convergente, non è assolutamente convergente: se i termini della serie vengono sistematicamente riarrangiati, in generale la somma diventa diversa e, a seconda del riarrangiamento, forse anche infinita.

La formula delle serie armoniche alternate è un caso particolare della serie Mercator, la serie Taylor per il logaritmo naturale.

Una serie correlata può essere derivata dalla serie di Taylor per l'arctangente:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\a6}}}{n=0}^{\a6}}{\a6}}{\a6}}{2n+1}}=1-{\a6}{\a6}+{\a6}}+{\a6}{5}}-{\a6}}{\a6}}++cdots ={\a6}{\a6}{\a6}}{\a6}{\a6}. } $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

Questa è conosciuta come la serie Leibniz.

Serie armoniche generali

La serie armonica generale è della forma

∑ n = 0 ∞ 1 a n + b , {\a6}}{n=0}^^infty \frac {1}{an+b},} $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

dove $a \neq 0$ e $b$ sono numeri reali, e b/a non è zero o un numero intero negativo.

Con la prova di confronto limite con le serie armoniche, anche tutte le serie armoniche generali divergono.

$serie p$

Una generalizzazione delle serie armoniche è la serie $p$ (o serie iperarmonica), definita come

∑ n = 1 ∞ 1 n n p {\a6}{n=1}^{\a6}{\a6}{\a6}{n^{p}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

per qualsiasi numero reale $p$ . Quando $p = 1$ , la $serie p$ è la serie armonica, che diverge. Sia la prova integrale che la prova di condensazione di Cauchy mostrano che la $serie p$ converge per tutte le $p > 1 ($ in questo caso si chiama serie sovraarmonica) e diverge per tutte le p ≤ $1.$ Se $p > 1$ allora la somma delle serie p è ζ( $p), cioè la$ funzione zeta di Riemann valutata a p.

Il problema di trovare la somma per $p = 2$ si chiama problema di Basilea; Leonhard Euler ha dimostrato che è π2/6. Il valore della somma per $p = 3$ è chiamato costante di Apéry, poiché Roger Apéry ha dimostrato che si tratta di un numero irrazionale.

In-serie

Relativa alla $serie p$ è la serie ln, definita come

∑ n = 2 ∞ 1 n ( ln n ) p {\a6}{n=2}^{\a6}{\a6}{\a6}{\a6}{\a6}{p}}}} $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

per qualsiasi numero reale positivo $p$ . Questo può essere mostrato dal test integrale per divergere per $p \leq 1$ ma convergere per tutti $p > 1.$

$φ-serie$

Per qualsiasi funzione convessa, con valore reale φ tale che

lim sup u → 0 + φ ( u 2) φ ( u ) φ ( u ) < 1 2 , \displaystyle \limsup _{u\frac {\fscx130\fscy130\frx40}{\fscy130\frx40}{\fscy130\frx40}{\fscy130\frx40}, \fscy130\frx40}{\fscy130\frx40}{\fscy130\frx40}{\fscy130\frx40}E' una cosa che non si può fare, ma che non si può fare. $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

la serie

∑ n = 1 ∞ φ ( 1 n ) {\a6}{n=1}^{\a6}{\a6}{\a6}{\a6}}varphi \a6}left(frac {\a6}{n}{n■destra)}{\a6}{\a6}{\a6} $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

è convergente. ^[]

Serie armonica casuale

La serie armonica casuale

∑ n = 1 ∞ s n n n , {\a6}{n=1}^infty ^frac {s_{n},} $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

dove gli $sn$ sono indipendenti, le variabili casuali distribuite in modo identico prendendo i valori +1 e -1 con uguale probabilità 1/2, è un esempio ben noto nella teoria delle probabilità per una serie di variabili casuali che convergono con la probabilità 1. Il fatto di questa convergenza è una facile conseguenza del teorema di Kolmogorov a tre serie o della disuguaglianza massima di Kolmogorov strettamente correlata. Byron Schmuland dell'Università di Alberta ha ulteriormente esaminato le proprietà delle serie armoniche casuali, e ha mostrato che la serie convergente è una variabile casuale con alcune proprietà interessanti. In particolare, la funzione di densità di probabilità di questa variabile casuale valutata a +2 o a -2 assume il valore 0,12499999999999999999999999999999999999999999999999764..., differendo da 1/8 per meno di 10-42. L'articolo di Schmuland spiega perché questa probabilità è così vicina, ma non esattamente, a 1/8. Il valore esatto di questa probabilità è dato dal prodotto infinito coseno integrale $C2$ diviso per π.

Serie armoniche esaurite

La serie armonica esaurita in cui sono stati eliminati tutti i termini in cui la cifra 9 appare in qualsiasi punto del denominatore può essere mostrata convergere e il suo valore è inferiore a 80. Infatti, quando tutti i termini contenenti una particolare stringa di cifre (in qualsiasi base) vengono rimossi, la serie converge.

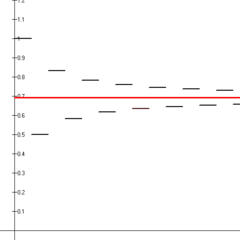
Le prime quattordici somme parziali delle serie armoniche alternate (segmenti di linea nera) mostrate convergono al logaritmo naturale di 2 (linea rossa).

Applicazioni

La serie armonica può essere controintuitiva. Questo perché si tratta di una serie divergente anche se i termini della serie diventano più piccoli e vanno verso lo zero. La divergenza delle serie armoniche è la fonte di alcuni paradossi.

Il "verme sull'elastico". Si supponga che un verme strisci lungo un elastico di un metro e mezzo di elastico all'infinito nello stesso momento in cui l'elastico viene allungato uniformemente. Se il verme viaggia di 1 centimetro al minuto e l'elastico si allunga di 1 metro al minuto, il verme raggiungerà mai la fine dell'elastico? La risposta, controintuitivamente, è "sì", perché dopo $n$ minuti, il rapporto tra la distanza percorsa dal verme e la lunghezza totale dell'elastico è

1 100 ∑ k = 1 n 1 k . Stile di visualizzazione {\an8}{100} {\an8} {\an8}{100}{k=1^{n}{frac {k}}. } ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Poiché la serie diventa arbitrariamente grande quando $n$ diventa più grande, alla fine questo rapporto deve superare 1, il che implica che il verme raggiunge la fine dell'elastico. Tuttavia, il valore di $n$ al quale ciò avviene deve essere estremamente grande: circa e100, un numero superiore a ¹⁰⁴³ minuti (¹⁰³⁷ anni). Anche se le serie armoniche divergono, lo fanno molto lentamente.

Il problema della Jeep chiede quanto carburante è necessario per un'auto con una limitata capacità di trasporto di carburante per attraversare un deserto lasciando cadere il carburante lungo il percorso. La distanza che l'auto può percorrere con una determinata quantità di carburante è legata alle somme parziali delle serie armoniche, che crescono logaritmicamente. E quindi il carburante richiesto aumenta in modo esponenziale con la distanza desiderata.

Il problema dell'impilamento a blocchi: data una collezione di tessere del domino identiche, è possibile impilarle sul bordo di un tavolo in modo che pendano dal bordo del tavolo senza cadere. Il risultato controintuitivo è che possono essere impilati in modo da rendere lo sbalzo grande quanto si vuole. Sempre che ci siano abbastanza tessere del domino.

Un nuotatore che va più veloce ogni volta che tocca la parete della piscina. Il nuotatore inizia ad attraversare una piscina di 10 metri ad una velocità di 2 m/s, e ad ogni attraversamento si aggiungono altri 2 m/s alla velocità. In teoria, la velocità del nuotatore è illimitata, ma il numero di attraversamenti della piscina necessari per raggiungere quella velocità diventa molto grande; ad esempio, per raggiungere la velocità della luce (ignorando la relatività speciale), il nuotatore deve attraversare la piscina 150 milioni di volte. Contrariamente a questo grande numero, il tempo necessario per raggiungere una data velocità dipende dalla somma delle serie a un dato numero di attraversamenti della piscina:

10 2 ∑ k = 1 n 1 k . {\an8}{2}}{2}{k=1^{n}{frac {1}{k}}. } ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Il calcolo della somma mostra che il tempo necessario per raggiungere la velocità della luce è di soli 97 secondi.

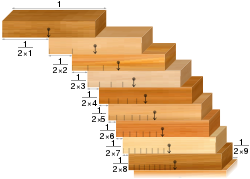
Il problema dell'accatastamento dei blocchi: blocchi allineati secondo la serie armonica di ponti di qualsiasi larghezza.

Pagine correlate

Progressione armonica
Elenco delle somme di reciproci

Domande e risposte

D: Cos'è la serie armonica?

R: La serie armonica è una serie divergente infinita in cui ogni termine è uguale a 1 diviso per la sua posizione nella sequenza.

D: Cosa significa che una serie è divergente?

R: Divergente significa che, aggiungendo altri termini, la somma non smette mai di aumentare e non si dirige verso un unico valore finito.

D: Cosa significa che una serie è infinita?

R: Infinita significa che si può sempre aggiungere un altro termine e che non c'è un termine finale alla serie.

D: Da dove deriva il nome di questa serie?

R: Il nome di questa serie deriva dall'idea delle armoniche nella musica, dove le lunghezze d'onda dei sovratoni sono 1/2, 1/3, 1/4, ecc. della lunghezza d'onda fondamentale della corda.

D: Che cos'è una media armonica?

R: Si parla di media armonica quando ogni termine di una sequenza è uguale alla media armonica dei termini vicini. Anche questa frase deriva dalla musica.

D: Come si calcola ogni termine di questa sequenza?

R: Ogni termine di questa sequenza può essere calcolato dividendo uno per la sua posizione nella sequenza (1/n).