Scala logaritmica
Una scala logaritmica è una scala utilizzata quando c'è una vasta gamma di quantità. Gli usi comuni includono la forza sismica, l'intensità del suono, l'intensità della luce e il pH delle soluzioni.
Si basa su ordini di grandezza, piuttosto che su una scala lineare standard. Il valore di ogni segno della scala è il valore del segno precedente moltiplicato per una costante.
Le scale logaritmiche sono anche utilizzate nei regoli calcolatori per moltiplicare o dividere i numeri aggiungendo o sottraendo lunghezze sulle scale.
La scala logaritmica può essere utile quando i dati coprono un ampio intervallo di valori - il logaritmo riduce questo ad un intervallo più gestibile.
Alcuni dei nostri sensi operano in modo logaritmico (moltiplicando l'effettiva potenza d'ingresso si aggiunge una costante alla potenza del segnale percepita, vedi: Legge di potenza di Stevens). Ciò rende le scale logaritmiche per queste quantità di ingresso particolarmente appropriate. In particolare, il nostro senso dell'udito percepisce multipli uguali di frequenze come differenze uguali di intonazione.
Nella maggior parte delle scale logaritmiche, piccoli multipli (o rapporti) della quantità sottostante corrispondono a piccoli valori (eventualmente negativi) della misura logaritmica.
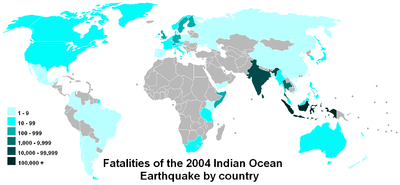
Una scala di log rende facile il confronto di valori che coprono un ampio intervallo, come in questa mappa
Le due scale logaritmiche di un regolo calcolatore
Esempi
Esempi ben noti di tali scale sono:
- Scala di magnitudo Richter e scala di magnitudo del momento (MMS) per la forza dei terremoti e il movimento della terra.
- bel e decibel e neper per la potenza acustica (loudness) e la potenza elettrica;
- conteggio degli f-stop per i rapporti di esposizione fotografica;
- valutare le basse probabilità in base al numero di 'nove' nell'espansione decimale della probabilità che non si verifichino: ad esempio, un sistema che si guasta con una probabilità di 10-5 è affidabile al 99,999%: "cinque nove".
- Entropia in termodinamica.
- Informazioni nella teoria dell'informazione.
- Curve di distribuzione granulometrica del terreno
Alcune scale logaritmiche sono state progettate in modo che grandi valori (o rapporti) della quantità sottostante corrispondano a piccoli valori della misura logaritmica. Esempi di tali scale sono:
- pH per l'acidità;
- scala di magnitudine stellare per la luminosità delle stelle;
Una scala logaritmica è anche una scala grafica su uno o entrambi i lati di un grafico dove un numero x è stampato ad una distanza c-log(x) dal punto segnato con il numero 1. Un regolo calcolatore ha scale logaritmiche, e i nomogrammi spesso utilizzano scale logaritmiche. Su una scala logaritmica una uguale differenza in ordine di grandezza è rappresentata da una uguale distanza. La media geometrica di due numeri è a metà strada tra i numeri.
La carta grafica logaritmica, prima dell'avvento della computer grafica, era uno strumento scientifico di base. I grafici su carta con una scala a log possono mostrare le leggi esponenziali, e su carta a log le leggi di potenza, come linee rette (vedi grafico a semilog, grafico a log).
Domande e risposte
D: Che cos'è una scala logaritmica?
R: La scala logaritmica è una scala utilizzata quando c'è un'ampia gamma di quantità.
D: Quali sono alcuni esempi di cose che possono essere misurate su una scala logaritmica?
R: La forza dei terremoti, il volume del suono, l'intensità della luce, il tasso di diffusione delle epidemie e il pH delle soluzioni possono essere misurati su una scala logaritmica.
D: In che modo una scala logaritmica è diversa da una scala lineare standard?
R: La scala logaritmica si basa sugli ordini di grandezza, piuttosto che sulla scala lineare standard. Il valore di ogni segno sulla scala è il valore del segno precedente moltiplicato per una costante.
D: Qual è il vantaggio di utilizzare una scala logaritmica?
R: La scala logaritmica può ridurre un'ampia gamma di valori a un intervallo più gestibile, il che può essere utile quando si tratta di dati che coprono un'ampia gamma di valori.
D: Cos'è la legge di potenza di Stevens e come si relaziona con le scale logaritmiche?
R: La legge di potenza di Stevens descrive come alcuni dei nostri sensi funzionino in modo logaritmico, dove la moltiplicazione dell'effettiva forza di ingresso aggiunge una costante alla forza del segnale percepito. Ciò rende le scale logaritmiche per queste quantità di input particolarmente appropriate.
D: Perché una scala logaritmica è particolarmente utile per misurare l'intensità del suono?
R: Il nostro senso dell'udito percepisce multipli uguali di frequenze come differenze uguali nell'altezza, quindi una scala logaritmica può rappresentare accuratamente questa relazione tra frequenza sonora e intensità percepita.
D: Qual è la relazione tra i piccoli multipli della quantità sottostante e la misura logaritmica sulla maggior parte delle scale logaritmiche?
R: Nella maggior parte delle scale logaritmiche, piccoli multipli (o rapporti) della quantità sottostante corrispondono a piccoli valori (eventualmente negativi) della misura logaritmica.
Cerca nell'enciclopedia