Regolo calcolatore

Concetti di base

Nella sua forma più elementare, il regolo calcolatore utilizza due scale logaritmiche per consentire una rapida moltiplicazione e divisione dei numeri. Queste operazioni comuni possono essere dispendiose in termini di tempo e soggette a errori se effettuate su carta. I regoli calcolatori più complessi consentono altri calcoli, come radici quadrate, esponenziali, logaritmi e funzioni trigonometriche.

I calcoli matematici vengono effettuati allineando un segno sulla striscia centrale scorrevole con uno su una delle strisce fisse. Si può quindi osservare la posizione relativa degli altri segni. I numeri allineati con i segni danno il valore approssimativo del prodotto, il quoziente, o altro risultato calcolato.

L'utente determina la posizione del punto decimale nel risultato, sulla base di una stima mentale. La notazione scientifica viene utilizzata per tracciare il punto decimale in calcoli più formali. Le fasi di addizione e sottrazione in un calcolo sono generalmente effettuate mentalmente o su carta, non sul regolo calcolatore.

La maggior parte dei regoli calcolatori ha tre strisce lineari della stessa lunghezza. Le strisce sono allineate in parallelo e interbloccate in modo che la striscia centrale possa essere spostata in senso longitudinale rispetto alle altre due. Le due strisce esterne sono fissate in modo che la loro posizione relativa non cambi.

Alcuni regoli calcolatori (modelli "duplex") hanno scale su entrambi i lati del regolo e della striscia di scorrimento, altri su un lato delle strisce esterne e su entrambi i lati della striscia di scorrimento, altri ancora su un solo lato (regole "simplex"). Un cursore a scorrimento con una linea di allineamento verticale viene utilizzato per trovare i punti corrispondenti su scale che non si trovano l'una accanto all'altra o, nei modelli duplex, sono sull'altro lato del regolo. Il cursore può anche registrare un risultato intermedio su una qualsiasi delle scale.

Cursore su regolo calcolatore

Utilizzo di un regolo calcolatore

Moltiplicazione

Un logaritmo trasforma le operazioni di moltiplicazione e divisione in addizione e sottrazione secondo le regole log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} e log ( x / y ) = log ( x ) - log ( y ) {\displaystyle \log(x/y)=\log(x)-\log(y)} . Spostare la scala in alto a destra di una distanza di log ( x ) {\displaystyle \log(x)}. facendo combaciare l'inizio della scala in alto con l'etichetta x {\displaystyle x} in basso, allinea ogni numero y {\displaystyle y} , al log di posizione ( y ) \displaystyle \log(y)} sulla scala superiore, con il numero al log di posizione ( x ) + log ( y ) \displaystyle \log(x)+ log(y)} sulla scala inferiore. Perché log ( x ) + log ( y ) = log ( x y ) {\postille \displaystyle \log(x)+\log(y)=\log(xy)}. questa posizione sulla scala inferiore dà x y {\i} il prodotto di x x e y.basso dove l'altro fattore è in alto.

Le operazioni possono andare "fuori scala"; ad esempio, il diagramma sopra mostra che il regolo calcolatore non ha posizionato il 7 sulla scala superiore al di sopra di qualsiasi numero sulla scala inferiore, quindi non dà alcuna risposta per 2×7. In questi casi, l'utente può far scorrere la scala superiore a sinistra fino a quando il suo indice destro non si allinea con il 2, moltiplicando di fatto per 0,2 invece che per 2, come nell'illustrazione sottostante:

Qui l'utente del regolo calcolatore deve ricordarsi di regolare il punto decimale in modo appropriato per correggere la risposta finale. Volevamo trovare 2×7, ma invece abbiamo calcolato 0,2×7=1,4. Quindi la risposta vera non è 1,4 ma 14. Il reset della diapositiva non è l'unico modo per gestire le moltiplicazioni che porterebbero a risultati fuori scala, come 2×7; alcuni altri metodi lo sono:

• (1) Utilizzare le scale a due decadi A e B.
• (2) Utilizzare la bilancia piegata. In questo esempio, impostare la sinistra 1 di C di fronte alla 2 di D. Spostare il cursore su 7 su CF, e leggere il risultato da DF.
• (3) Utilizzare la scala invertita CI. Posizionare il 7 sulla scala CI sopra il 2 sulla scala D, e poi leggere il risultato fuori dalla scala D, sotto il 1 sulla scala CI. Poiché 1 si verifica in due punti della scala CI, uno di essi sarà sempre in scala.
• (4) Utilizzare sia la scala CI invertita che la scala C. Allineare il 2 di CI con l'1 di D, e leggere il risultato da D, sotto il 7 della scala C.

Il metodo 1 è facile da capire, ma comporta una perdita di precisione. Il metodo 3 ha il vantaggio che comporta solo due scale.

Divisione

L'illustrazione sottostante mostra il calcolo di 5,5/2. Il 2 sulla scala superiore è posto sopra il 5,5 sulla scala inferiore. Il 1 sulla scala superiore si trova sopra il quoziente, 2,75. C'è più di un metodo per fare la divisione, ma il metodo qui presentato ha il vantaggio che il risultato finale non può essere fuori scala, perché si può scegliere di usare l'1 ad entrambe le estremità.

Altre operazioni

Oltre alle scale logaritmiche, alcuni regoli calcolatori hanno altre funzioni matematiche codificate su altre scale ausiliarie. Le più popolari erano le scale trigonometriche, di solito sinusoidali e tangenti, il logaritmo comune (log10) (per prendere il log di un valore su una scala moltiplicatrice), il logaritmo naturale (ln) e le scale esponenziali (^ex). Alcune regole includono una scala pitagorica, per figurare i lati dei triangoli, e una scala per figurare i cerchi. Altre sono dotate di scale per il calcolo delle funzioni iperboliche. Sulle regole lineari, le scale e la loro etichettatura sono altamente standardizzate, con variazioni che di solito si verificano solo in termini di quali scale sono incluse e in quale ordine:

A, B	scale logaritmiche a due decadi, utilizzate per trovare radici quadrate e quadrati di numeri
C, D	scale logaritmiche a un decennio
K	scala logaritmica a tre decadi, utilizzata per trovare radici a cubo e cubi di numeri
CF, DF	versioni "piegate" delle scale C e D che partono da π piuttosto che dall'unità; queste sono convenienti in due casi. In primo luogo, quando l'utente indovina che un prodotto sarà vicino a 10 ma non è sicuro se sarà leggermente inferiore o leggermente superiore a 10, le scale piegate evitano la possibilità di uscire dalla scala. In secondo luogo, facendo l'inizio π piuttosto che la radice quadrata di 10, si semplifica la moltiplicazione o la divisione per π (come è comune nelle formule scientifiche e ingegneristiche).
CI, DI, DIF	scale "invertite", da destra a sinistra, utilizzate per semplificare i passi 1/x
S	usato per trovare i seni e i coseni sulla scala D
T	utilizzato per trovare tangenti e cotangenti sulle scale D e DI
ST, SRT	utilizzato per i seni e le tangenti di piccoli angoli e per la conversione gradi-radiana
L	una scala lineare, utilizzata insieme alle scale C e D per trovare logaritmi di base 10 e potenze di 10
LLn	una serie di scale log-log, utilizzate per trovare logaritmi ed esponenziali dei numeri
Ln	una scala lineare, usata insieme alle scale C e D per trovare i logaritmi naturali (base e) e e x {\fscx130\fscy130\frx40}}e x

 

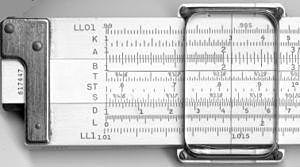
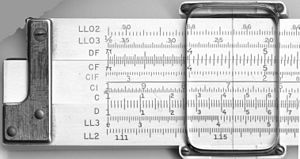
Le scale sul fronte e sul retro di un regolo calcolatore K&E 4081-3.

Il Binary Slide Rule prodotto da Gilson nel 1931 svolgeva una funzione di addizione e sottrazione limitata alle frazioni.

Radici e poteri

Ci sono scale a un decennio (C e D), a due decenni (A e B) e a tre decenni (K). Per calcolare x 2 {\i}{2}} ad esempio, individuare x sulla scala D e leggere il suo quadrato sulla scala A. Invertendo questo processo si possono trovare le radici quadrate, e in modo simile per le potenze 3, 1/3, 2/3 e 3/2. Bisogna fare attenzione quando la base, x, si trova in più di un punto della scala. Per esempio, ci sono due nove sulla scala A; per trovare la radice quadrata di nove, usare la prima; la seconda dà la radice quadrata di 90.

Per i problemi di x y, usare la scala LL. Quando sono presenti diverse scale LL, usare quella con x. Per prima cosa, allineare il più a sinistra di 1 sulla scala C con x sulla scala LL. Poi, trovare y sulla scala C e scendere alla scala LL con x su di essa. Questa scala indicherà la risposta. Se y è "fuori dalla scala", individuare x y / 2 {\i} e squadrarla usando le scale A e B come descritto sopra.

Trigonometria

Le scale S, T e ST sono utilizzate per funzioni trigonometriche e multipli di funzioni trigonometriche, per angoli in gradi. Molti regoli calcolatori hanno le loro scale S, T e ST contrassegnate con gradi e minuti. I cosiddetti modelli di decitrigo utilizzano invece frazioni decimali di gradi.

Logaritmi ed esponenziali

I logaritmi e gli esponenziali di base 10 si trovano utilizzando la scala L, che è lineare. Alcuni regoli calcolatori hanno una scala Ln, che è per la base e.

La scala Ln è stata inventata da uno studente dell'undicesimo anno, Stephen B. Cohen, nel 1958. L'intento originale era quello di permettere all'utente di selezionare un esponente x (nel range da 0 a 2.3) sulla scala Ln e di leggere ^{ex sulla} scala C (o D) e ^e-x sulla scala CI (o DI). Pickett, Inc. ha ottenuto l'esclusiva della scala. In seguito, l'inventore ha creato una serie di "marchi" sulla scala Ln per estendere il campo oltre il limite 2.3, ma Pickett non ha mai incorporato questi marchi su nessuno dei suoi regoli calcolatori. ^[]

Aggiunta e sottrazione

Le slide rules non sono tipicamente utilizzate per addizione e sottrazione, ma è comunque possibile farlo utilizzando due diverse tecniche.

Il primo metodo per eseguire addizione e sottrazione sulle scale C e D (o su qualsiasi scala comparabile) richiede la conversione del problema in una di divisione. Per l'addizione, il quoziente delle due variabili più una volta il divisore è uguale alla loro somma:

x + y = ( x y + 1 ) y {\displaystyle x+y=\frac {x}{y}}+1\destra)y

Per sottrazione, il quoziente delle due variabili meno una volta il divisore è uguale alla loro differenza:

x - y = ( x y - 1 ) y {\a6} y {\a6}}[x - y - 1 ) y {\a6}[x - y = ( x y - 1 )] y

Questo metodo è simile alla tecnica di addizione/sottrazione utilizzata per i circuiti elettronici ad alta velocità con il sistema di numeri logaritmici in applicazioni informatiche specializzate come il supercomputer Gravity Pipe (GRAPE) e i modelli Markov nascosti.

Il secondo metodo utilizza una scala lineare scorrevole a L disponibile su alcuni modelli. L'addizione e la sottrazione vengono eseguite facendo scorrere il cursore a sinistra (per la sottrazione) o a destra (per l'addizione) e poi riportando la diapositiva a 0 per leggere il risultato.

Progettazione fisica

Regole lineari standard

La lunghezza del regolo calcolatrice viene indicata in termini di lunghezza nominale delle scale. Le scale dei più comuni modelli da "10 pollici" sono in realtà lunghe 25 cm, in quanto sono state realizzate secondo gli standard metrici, anche se alcune regole offrono scale leggermente estese per semplificare la manipolazione quando un risultato trabocca. Le regole tascabili sono tipicamente di 5 pollici. I modelli lunghi un paio di metri sono stati venduti per essere appesi nelle aule per scopi didattici. [1]

Tipicamente le divisioni segnano una scala con una precisione di due cifre significative, e l'utente stima la terza cifra. Alcuni regoli calcolatori di fascia alta hanno cursori di ingrandimento che rendono le marcature più facili da vedere. Tali cursori possono effettivamente raddoppiare la precisione delle letture, permettendo ad un regolo calcolatore da 10 pollici di servire così come ad un regolo calcolatore da 20 pollici.

Sono state sviluppate diverse altre comodità. Le scale trigonometriche sono a volte a doppia etichettatura, in nero e rosso, con angoli complementari, il cosiddetto stile "Darmstadt". I regoli calcolatori duplex spesso duplicano alcune delle scale sul retro. Le scale sono spesso "divise" per ottenere una maggiore precisione.

Sono stati inventati regoli calcolatori specializzati per varie forme di ingegneria, affari e banche. Queste spesso avevano calcoli comuni direttamente espressi come scale speciali, per esempio calcoli di prestiti, quantità di acquisto ottimali o particolari equazioni ingegneristiche. Ad esempio, la società Fisher Controls ha distribuito un regolo calcolatore personalizzato adattato per risolvere le equazioni utilizzate per la selezione delle dimensioni corrette delle valvole di controllo del flusso industriale. ^[]

Regoli calcolatori circolari

I regoli calcolatori circolari sono disponibili in due tipi di base, uno con due cursori (a sinistra) e un altro con un disco mobile e un singolo cursore (a destra). Le versioni a doppio cursore eseguono la moltiplicazione e la divisione mantenendo un angolo fisso tra i cursori mentre vengono ruotati intorno al quadrante. La versione a cursore singolo funziona più come il regolo calcolatore standard attraverso l'allineamento appropriato delle scale.

Il vantaggio fondamentale di un regolo calcolatore circolare è che la dimensione più lunga dell'utensile è stata ridotta di un fattore di circa 3 (cioè di π). Ad esempio, la scala esterna di un regolo calcolatore circolare di 10 cm avrebbe una precisione massima pari a quella di un regolo calcolatore ordinario di 30 cm. I regoli calcolatori circolari eliminano anche i calcoli "fuori scala", perché le scale sono state progettate per "avvolgere"; non devono mai essere riorientate quando i risultati sono vicini a 1,0 - il regolo è sempre in scala. Tuttavia, per le scale non cicliche non a spirale come S, T e LL, la lunghezza della scala è ridotta per fare spazio ai margini finali.

I regoli calcolatori circolari sono meccanicamente più robusti e più scorrevoli, ma la loro precisione di allineamento della scala è sensibile al centraggio di un perno centrale; un minuto di 0,1 mm di distanza dal centro del perno può causare un errore di allineamento di 0,2 mm nel caso peggiore. Il perno, tuttavia, evita di graffiare il viso e i cursori. Le scale di massima precisione sono posizionate sugli anelli esterni. Piuttosto che su scale "split", le regole circolari di fascia alta utilizzano scale a spirale per operazioni più complesse come le scale log-of-log. Una regola circolare premium da otto pollici aveva una scala a spirale log-log da 50 pollici.

I principali svantaggi dei regoli calcolatori circolari sono la difficoltà di individuare le figure lungo un disco rotante e il numero limitato di scale. Un altro svantaggio dei regoli calcolatori circolari è che le scale meno importanti sono più vicine al centro e hanno precisioni inferiori. La maggior parte degli studenti ha imparato ad usare il regolo calcolatore sui regoli calcolatori lineari e non ha trovato motivo di cambiare.

Un regolo calcolatore rimasto in uso quotidiano in tutto il mondo è l'E6B. Si tratta di un regolo calcolatore circolare creato per la prima volta negli anni '30 per aiutare i piloti di aerei a fare i conti con la morte. Con l'aiuto di scale stampate sul telaio aiuta anche in compiti vari come la conversione di tempo, distanza, velocità e valori di temperatura, errori della bussola e il calcolo del consumo di carburante. La cosiddetta "ruota della preghiera" è ancora disponibile nei negozi di volo e rimane ampiamente utilizzata. Mentre il GPS ha ridotto l'uso del calcolo morto per la navigazione aerea, e le calcolatrici portatili hanno assunto molte delle sue funzioni, l'E6B rimane ampiamente utilizzato come dispositivo primario o di backup e la maggior parte delle scuole di volo richiede ai propri studenti un certo grado di padronanza.

Nel 1952 l'azienda orologiera svizzera Breitling ha introdotto un orologio da polso per piloti con regolo calcolatore circolare integrato specializzato nel calcolo del volo: il Breitling Navitimer. Il regolo circolare Navitimer, definito da Breitling "computer di navigazione", presentava funzioni di velocità dell'aria, velocità/tempo di salita/discesa, tempo di volo, distanza e consumo di carburante, nonché funzioni di conversione della quantità di carburante in chilometri e litri di carburante.

Materiali

Tradizionalmente i regoli calcolatori erano fatti di legno duro come il mogano o il bosso con cursori di vetro e metallo. Almeno uno strumento di alta precisione era fatto di acciaio.

Nel 1895, una ditta giapponese, la Hemmi, iniziò a produrre regoli calcolatori in bambù, che avevano il vantaggio di essere dimensionalmente stabili, forti e naturalmente autolubrificanti. Questi regoli calcolatori di bambù furono introdotti in Svezia nel settembre del 1933 [2], e probabilmente solo poco prima in Germania. Le scale erano fatte di celluloide o di plastica. Più tardi i regoli calcolatori furono fatti di plastica, o di alluminio verniciato con la plastica. I cursori successivi erano in acrilico o policarbonato che scorrevano su cuscinetti in teflon.

Tutti i regoli calcolatori premium avevano numeri e scale incisi e poi riempiti con vernice o altra resina. I regoli calcolatori verniciati o stampati erano considerati inferiori perché le marcature potevano svanire. Tuttavia, Pickett, probabilmente l'azienda americana di maggior successo nel settore dei regoli calcolatori, ha realizzato tutti i regoli calcolatori stampati. Tra i regoli calcolatori di qualità superiore vi erano anche grimaldelli intelligenti, in modo che il regolo non cadesse a pezzi per caso, e paraurti per proteggere le bilance e il cursore dallo sfregamento sui piani dei tavoli. Il metodo di pulizia consigliato per le marcature incise è quello di strofinare leggermente con lana d'acciaio. Per i regoli calcolatori verniciati, e per i deboli di cuore, utilizzare un liquido detergente per vetri commerciale diluito e un panno morbido.

Regolo calcolatore circolare Pickett con due cursori. (diametro 4,25 in./10,9 cm) Reverse ha una scala supplementare e un cursore.


Un semplice regolo calcolatore circolare, realizzato dalla Concise Co., Ltd., Tokyo, Giappone, con sole scale inverse, quadrate e cubiche. Sul retro è riportato un comodo elenco di 38 fattori di conversione metrico/imperiale.


Orologio da polso Breitling Navitimer con regolo calcolatore circolare

Storia

Il regolo calcolatore fu inventato intorno al 1620-1630, poco dopo la pubblicazione del concetto di logaritmo da parte di John Napier. Edmund Gunter di Oxford sviluppò un dispositivo di calcolo con un'unica scala logaritmica, che, con strumenti di misura aggiuntivi, poteva essere utilizzato per moltiplicare e dividere. La prima descrizione di questa scala fu pubblicata a Parigi nel 1624 da Edmund Wingate (c. 1593 - 1656), un matematico inglese, in un libro intitolato "L'usage de la reigle de proportion en l'arithmetique & geometrie". Il libro contiene una doppia scala, da un lato una scala logaritmica e dall'altro una scala tabulare. Nel 1630, William Oughtred di Cambridge inventò un regolo calcolatore circolare, e nel 1632 combinò due regole Gunter, tenute insieme con le mani, per realizzare un dispositivo che è riconoscibile come il regolo calcolatore moderno. Come il suo contemporaneo a Cambridge, Isaac Newton, Oughtred insegnò le sue idee in privato ai suoi studenti, ma ritardò a pubblicarle e, come Newton, fu coinvolto in una controversia al vetriolo sulla priorità, con il suo ex studente Richard Delamain e le precedenti affermazioni di Wingate. Le idee di Oughtred furono rese pubbliche solo nelle pubblicazioni del suo allievo William Forster nel 1632 e nel 1653.

Nel 1677, Henry Coggeshall creò un regolo pieghevole di due piedi per la misura del legno, chiamato regolo calcolatore Coggeshall. Il suo progetto e l'uso di questo strumento ha dato al regolo calcolatore uno scopo al di fuori della ricerca matematica.

Nel 1722, Warner introdusse le scale a due e tre decadi, e nel 1755 Everard incluse una scala invertita; un regolo calcolatore contenente tutte queste scale è solitamente conosciuto come regola "polifase".

Nel 1815, Peter Roget inventò il regolo calcolatore per tronchi di legno, che comprendeva una scala che mostrava il logaritmo del logaritmo. Questo permetteva all'utente di eseguire direttamente i calcoli che coinvolgevano radici ed esponenti. Questo era particolarmente utile per le potenze frazionarie.

Forma moderna

La forma più moderna fu creata nel 1859 dal tenente d'artiglieria francese Amédée Mannheim, "che ebbe la fortuna di farsi fare il suo dominio da una ditta di fama nazionale e di farla adottare dall'artiglieria francese". Fu in quel periodo, quando l'ingegneria divenne un'attività professionale riconosciuta, che i regoli calcolatori entrarono in uso in Europa. Non divennero comuni negli Stati Uniti fino al 1881, quando Edwin Thacher vi introdusse un regolo cilindrico. Il regolo duplex fu inventato da William Cox nel 1891, e fu prodotto dalla Keuffel e dalla Esser Co. di New York.

Anche il lavoro astronomico richiedeva calcoli di precisione, e nella Germania del 19° secolo un regolo calcolatore in acciaio lungo circa 2 metri è stato utilizzato in un osservatorio. Aveva un microscopio attaccato, che gli dava una precisione di sei cifre decimali.

Nella seconda guerra mondiale, i bombardieri e i navigatori che richiedevano calcoli rapidi utilizzavano spesso regoli calcolatori specializzati. Un ufficio della Marina degli Stati Uniti ha effettivamente progettato un generico "telaio" del regolo calcolatore con un corpo in alluminio e un cursore in plastica in cui potevano essere inserite delle schede di celluloide (stampate su entrambi i lati) per calcoli speciali. Il processo fu inventato per calcolare l'autonomia, l'uso di carburante e l'altitudine degli aerei, e poi adattato a molti altri scopi.

Per tutti gli anni '50 e '60 il regolo calcolatore è stato il simbolo della professione di ingegnere (così come lo stetoscopio simboleggia la professione medica). ^{[] Lo} scienziato missilistico tedesco Wernher von Braun portò con sé due regoli calcolatori Nestler d'epoca degli anni '30 quando si trasferì negli Stati Uniti dopo la seconda guerra mondiale per lavorare al programma spaziale americano. In tutta la sua vita non ha mai usato altri dispositivi di calcolo tascabili; i regoli calcolatori gli sono serviti perfettamente per fare stime rapide dei parametri di progettazione dei razzi e di altri dati. I regoli calcolatori in alluminio a marchio Pickett-brand sono stati trasportati in cinque missioni spaziali Apollo, anche sulla Luna, secondo la pubblicità sulle scatole di regoli calcolatori N600 di Pickett [3].

Alcuni studenti di ingegneria e ingegneri portavano regoli calcolatori da dieci pollici in fondine da cintura, e anche a metà degli anni '70 questo era uno spettacolo comune nei campus. Gli studenti potevano anche tenere un regolo calcolatore da dieci o venti pollici per il lavoro di precisione a casa o in ufficio, portando con sé un regolo calcolatore tascabile da cinque pollici.

Nel 2004, i ricercatori nel campo dell'istruzione David B. Sher e Dean C. Nataro hanno concepito un nuovo tipo di regolo calcolatore basato sulla protesizzazione, un algoritmo per prodotti di calcolo rapido che precede i logaritmi. C'è stato però poco interesse pratico a costruirne uno oltre il prototipo iniziale. [4]

Diminuire

L'importanza del regolo calcolatore iniziò a diminuire man mano che i computer elettronici, una risorsa nuova ma molto scarsa negli anni '50, divennero ampiamente disponibili per gli operai tecnici durante gli anni '60. L'introduzione del Fortran nel 1957 ha reso i computer pratici per risolvere problemi matematici di modeste dimensioni. La IBM introdusse una serie di computer più convenienti, l'IBM 650 (1954), l'IBM 1620 (1959), l'IBM 1130 (1965) destinati al mercato della scienza e dell'ingegneria. Il linguaggio di programmazione BASIC di John Kemeny (1964) rese facile l'uso dei computer per gli studenti. Il minicomputer DEC PDP-8 fu introdotto nel 1965.

I computer hanno anche cambiato la natura del calcolo. Con i regoli calcolatori, c'è stata una grande enfasi sul lavoro dell'algebra per ottenere espressioni nella forma più calcolabile. Gli utenti dei regoli calcolatori si limitavano ad approssimare o a tralasciare piccoli termini per semplificare il calcolo. Fortran permetteva di digitare formule complicate dai libri di testo senza lo sforzo di riformulazione. L'integrazione numerica era spesso più facile che cercare di trovare soluzioni in forma chiusa per problemi difficili. Il giovane ingegnere che chiedeva tempo al computer per risolvere un problema che avrebbe potuto essere risolto con qualche strisciata sul regolo calcolatore divenne un cliché umoristico. Molti centri di calcolo avevano un regolo calcolatore incorniciato appeso al muro con la scritta "In caso di emergenza, rompere il vetro".

Un altro passo verso la sostituzione dei regoli calcolatori con l'elettronica è stato lo sviluppo di calcolatrici elettroniche per uso scientifico e ingegneristico. La prima comprendeva i Wang Laboratories LOCI-2, introdotti nel 1965, che utilizzavano i logaritmi per la moltiplicazione e la divisione e la Hewlett-Packard HP-9100, introdotta nel 1968. L'HP-9100 aveva funzioni trigonometriche (peccato, cos, abbronzatura) oltre ad esponenziali e logaritmi. Utilizzava l'algoritmo CORDIC (coordinate rotation digital computer), che permette di calcolare le funzioni trigonometriche utilizzando solo le operazioni di spostamento e di aggiunta. Questo metodo ha facilitato lo sviluppo di calcolatrici scientifiche sempre più piccole.

L'ultimo chiodo nella bara per il regolo calcolatore è stato il lancio delle calcolatrici scientifiche tascabili, di cui la Hewlett-Packard HP-35 del 1972 è stata la prima. Tali calcolatrici divennero note come calcolatrici a "regolo calcolatore", poiché potevano eseguire la maggior parte o tutte le funzioni di un regolo calcolatore. A diverse centinaia di dollari, anche questa era considerata costosa per la maggior parte degli studenti. Mentre i regoli calcolatori professionali potevano anche essere abbastanza costosi, le farmacie spesso vendevano modelli di base in plastica per meno di 20 dollari. Ma entro il 1975, le calcolatrici elettroniche di base a quattro funzioni potevano essere acquistate a meno di 50 dollari. Nel 1976 la TI-30 offriva una calcolatrice scientifica per meno di 25 dollari. Dopo questo periodo, il mercato dei regoli calcolatori si prosciugò rapidamente, poiché le piccole calcolatrici scientifiche divennero accessibili.

William Oughtred (1575-1660), inventore del regolo calcolatore circolare


Ingegnere che usa un regolo calcolatore. Nota la calcolatrice meccanica in background.


TI-30

Vantaggi

• Un regolo calcolatore tende a moderare la fallacia della "falsa precisione" e del significato. La precisione tipica a disposizione di un utilizzatore di un regolo calcolatore è di circa tre punti di precisione. Ciò è in buona corrispondenza con la maggior parte dei dati disponibili per l'inserimento di formule di ingegneria. Quando si usa una moderna calcolatrice tascabile, la precisione può essere visualizzata con sette o più decimali, mentre in realtà i risultati non possono mai essere più precisi dei dati di input disponibili.
• Un regolo calcolatore richiede una stima continua dell'ordine di grandezza dei risultati. Su un regolo calcolatore 1,5 × 30 (che equivale a 45) mostrerà lo stesso risultato di 1.500.000 × 0,03 (che equivale a 45.000). Spetta all'ingegnere determinare continuamente la ragionevolezza dei risultati, cosa che può andare persa quando i numeri vengono inseriti con noncuranza in un programma per computer o in una calcolatrice.
• Quando si esegue una sequenza di moltiplicazioni o divisioni per lo stesso numero, la risposta può essere spesso determinata semplicemente guardando il regolo calcolatore senza alcuna manipolazione. Ciò può essere particolarmente utile quando si calcolano le percentuali, ad esempio per i punteggi dei test, o quando si confrontano i prezzi, ad esempio, in dollari per chilogrammo. Con un regolo calcolatore si possono eseguire a colpo d'occhio calcoli multipli velocità-tempo-distanza a mani libere con un regolo calcolatore.
• Un regolo calcolatore non dipende dall'elettricità.
• Un regolo calcolatore è una tecnologia facilmente replicabile. Da un dato esempio di regolo calcolatore, un artigiano competente può costruirne altri da materiali rudimentali utilizzando processi non industriali.
• Le regole di scorrimento sono altamente standardizzate, quindi non c'è bisogno di riapprendere nulla quando si passa a una regola diversa.
• I regoli di scorrimento sono versatili e possono essere utilizzati in situazioni e ambienti in cui un utente umano potrebbe avere una ridotta destrezza (ad esempio, a causa della necessità di guanti protettivi). Al contrario, una calcolatrice può essere difficile da utilizzare in tali situazioni - è improbabile che un regolo calcolatore dia luogo ad un errore simile a quello derivante dall'errata pressione del pulsante sbagliato su una calcolatrice.
• I regoli di scorrimento possono essere realizzati in cartone o carta. Molti diagrammi gratuiti o dispositivi di calcolo specializzati fatti di cartone sono in realtà regoli calcolatori lineari o circolari specializzati.

Un vantaggio dell'uso di un regolo calcolatore elettronico insieme ad una calcolatrice elettronica è che un calcolo importante può essere controllato facendo su entrambi; poiché i due strumenti sono così diversi, ci sono poche possibilità di commettere lo stesso errore due volte.

Pagine correlate

• Gli errori possono derivare da imprecisioni meccaniche.
• I calcoli con il regolo calcolatore sono di precisione limitata a causa dei loro ingressi e uscite analogiche. Al contrario, a causa dell'ingresso numerico discreto e delle operazioni elettroniche a virgola mobile, anche modeste calcolatrici moderne hanno risoluzioni di uscita di almeno sei cifre significative.

[
{[91103-70509]}]

• Abacus
• Logaritmo