Linea di universo
Una linea del mondo è il percorso unico che un oggetto ha mentre viaggia attraverso lo spazio e il tempo, solitamente chiamato spaziotempo. Come impariamo dalla relatività speciale, più un oggetto va veloce, più il tempo rallenta per quell'oggetto. Come si può vedere nell'illustrazione a destra, l'oggetto più lento ha un passaggio di tempo più veloce dell'oggetto molto veloce, quello per cui il tempo passa molto più lentamente. Quando un oggetto raggiunge la velocità della luce, sarà zero sull'asse t, il che significa che non avrà fatto alcun progresso nella direzione del tempo. Fondamentalmente, le linee del mondo mostrano che quando si raggiunge la velocità della luce, il tempo si ferma per l'osservatore. Le linee del mondo sono usate molto spesso nella fisica teorica e nella relatività speciale, così come nella relatività generale.
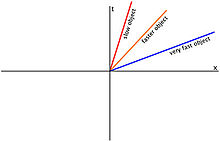
I percorsi distinti di tre oggetti che vanno a velocità diverse e le loro rispettive misure del passaggio del tempo, dove l'asse t rappresenta il passaggio del tempo e l'asse x rappresenta la velocità dell'oggetto.
Uso
Il concetto di linee del mondo è molto usato nella fisica teorica, perché mostra alcuni fatti interessanti sul movimento ad alta velocità. Per esempio, l'equazione di dilatazione del tempo presentata da Albert Einstein è algebricamente indefinita quando la velocità di un oggetto è la velocità della luce, ma usando le linee del mondo si può trovare che quando la velocità è la velocità della luce, il tempo si ferma. Anche se l'equazione di Einstein (per la dilatazione del tempo) mostra che un oggetto che va più veloce della luce va indietro nel tempo, lo stesso concetto può essere descritto usando le linee del mondo.
| Parte di una serie di articoli su | ||||||
| Relatività generale | ||||||
|
G μ ν + Λ g μ ν = 8 π G c 4 T μ ν {\displaystyle G_{\mu \nu }+Lambda g_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu }} | ||||||
| ·
·
| ||||||
| Concetti fondamentali
| ||||||
| Fenomeni
| ||||||
| ||||||
| Soluzioni
| ||||||
| · v · t · e |
Domande e risposte
D: Cos'è una linea del mondo?
R: Una linea del mondo è il percorso unico di un oggetto che viaggia nello spazio e nel tempo, solitamente chiamato spaziotempo.
D: In che modo la relatività speciale spiega come passa il tempo per gli oggetti che viaggiano a velocità diverse?
R: Secondo la relatività speciale, più un oggetto va veloce, più il tempo rallenta per quell'oggetto. L'oggetto più lento ha un passaggio di tempo più rapido rispetto all'oggetto molto veloce, il che significa che il tempo passa molto più lentamente per loro.
D: Cosa succede quando un oggetto raggiunge la velocità della luce?
R: Quando un oggetto raggiunge la velocità della luce, si troverà a zero sull'asse t, il che significa che non avrà fatto alcun progresso nella direzione del tempo. Ciò significa che il tempo si ferma per l'osservatore.
D: In quali settori vengono utilizzate le linee del mondo?
R: Le linee del mondo sono molto utilizzate nella fisica teorica e nella relatività speciale, oltre che nella relatività generale.
D: Come possiamo visualizzare una linea del mondo?
R: Possiamo visualizzare una linea del mondo guardando le illustrazioni che mostrano come gli oggetti che viaggiano a velocità diverse sperimentano tassi diversi di passaggio del tempo.
D: C'è un modo per cambiare o alterare una linea del mondo una volta stabilita?
R: Una volta stabilita una linea del mondo, non può essere cambiata o alterata, poiché rappresenta un percorso immutabile attraverso lo spaziotempo.
D: A cosa si riferisce l'"asse t" per quanto riguarda il raggiungimento della velocità della luce? R: L'"asse t" si riferisce al progresso in termini di tempo - quando un oggetto raggiunge la velocità della luce, il suo progresso in termini di tempo è pari a zero su questo asse, il che significa che non è stato fatto alcun progresso in termini di passaggio attraverso lo spazio-tempo.
Cerca nell'enciclopedia

