Algebra

L'algebra (dall'arabo: الجبر, traslitterato "al-jabr", che significa "riunione di parti rotte") fa parte della matematica (spesso chiamata matematica negli Stati Uniti e matematica o calcolo numerico nel Regno Unito). Utilizza variabili per rappresentare un valore che non è ancora noto. Quando si usa un segno uguale (=), questo viene chiamato equazione. Un'equazione molto semplice che utilizza una variabile è: 2 + 3 = x. In questo esempio, x = 5, o si potrebbe anche dire che "x è uguale a cinque". Questo si chiama risolvere per x.

Oltre alle equazioni, ci sono disuguaglianze (minori e maggiori). Un tipo speciale di equazione è chiamata funzione. Questa è spesso usata nella realizzazione di grafici, perché trasforma sempre un ingresso in un'uscita.

L'algebra può essere usata per risolvere problemi reali perché le regole dell'algebra funzionano nella vita reale e i numeri possono essere usati per rappresentare i valori delle cose reali. La fisica, l'ingegneria e la programmazione informatica sono aree che utilizzano l'algebra in continuazione. È utile anche conoscere nel rilievo, nell'edilizia e nel commercio, soprattutto nella contabilità.

Le persone che fanno algebra usano le regole dei numeri e le operazioni matematiche usate sui numeri. Le più semplici sono aggiungere, sottrarre, moltiplicare e dividere. Le operazioni più avanzate coinvolgono gli esponenti, a partire dai quadrati e dalle radici quadrate.

L'algebra è stata utilizzata per risolvere equazioni e disuguaglianze. Due esempi sono le equazioni lineari (l'equazione di una retta, y=mx+b) e le equazioni quadratiche, che ha variabili che sono al quadrato (moltiplicato per se stesso, per esempio: 2*2, 3*3, o x*x).

Storia

Le prime forme di algebra furono sviluppate dai Babilonesi e dai geometri greci come Eroe di Alessandria. Tuttavia la parola "algebra" è una forma latina della parola araba Al-Jabr ("fusione") e deriva da un libro di matematica Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah, ("Saggio sul calcolo della fusione e dell'equazione") scritto nel IX secolo da un matematico persiano, Muhammad ibn Mūsā al-Khwārizmī, musulmano nato a Khwarizm in Uzbekistan. Fiorì sotto Al-Ma'moun a Baghdad, in Iraq, fino all'813-833 d.C., e morì intorno all'840 d.C.. Il libro fu portato in Europa e tradotto in latino nel XII secolo. Al libro fu poi dato il nome di "Algebra". (La fine del nome del matematico, al-Khwarizmi, fu cambiata in una parola più facile da dire in latino, e divenne l'algoritmo della parola inglese).

Esempi

Ecco un semplice esempio di problema di algebra:

Sue ha 12 caramelle, e Ann ne ha 24. Decidono di condividere in modo da avere lo stesso numero di caramelle. Quante caramelle avranno ciascuna?

Questi sono i passi che potete utilizzare per risolvere il problema:

Per avere lo stesso numero di caramelle, Ann deve darne un po' a Sue. Lasciate che x rappresenti il numero di caramelle che Ann dà a Sue.
Le caramelle di Sue, più x, devono essere uguali alle caramelle di Ann meno x. Questo è scritto come: 12 + x = 24 - x
Sottrarre 12 da entrambi i lati dell'equazione. Questo dà: x = 12 - x. (Ciò che accade da un lato del segno di uguale deve accadere anche dall'altro lato, perché l'equazione sia ancora vera. Quindi in questo caso quando 12 è stato sottratto da entrambi i lati, c'è stato un passo intermedio di 12 + x - 12 = 24 - x - 12. Dopo che una persona è a suo agio con questo, il passo intermedio non viene scritto).
Aggiungere x a entrambi i lati dell'equazione. Questo dà: 2x = 12
Dividere entrambi i lati dell'equazione per 2. Questo dà x = 6. La risposta è sei. Se Ann dà a Sue 6 caramelle, avranno lo stesso numero di caramelle.
Per verificare questo, rimettere 6 nell'equazione originale ovunque x fosse: 12 + 6 = 24 - 6
Questo dà 18=18, che è vero. Ora ognuno di loro ha 18 caramelle.

Con la pratica, l'algebra può essere utilizzata quando ci si trova di fronte a un problema troppo difficile da risolvere in altro modo. Problemi come la costruzione di un'autostrada, la progettazione di un telefono cellulare o la ricerca di una cura per una malattia richiedono tutti l'algebra.

Algebra di scrittura

Come nella maggior parte delle parti della matematica, l'aggiunta di z a y (o y più z) è scritta come y + z. Sottrarre z da y (o y meno z) è scritto come y - z. Dividere y per z (o y su z: y z {\i} ${y \over z}$ ) è scritto come y ÷ z o y/z. y/z è più comunemente usato.

In algebra, moltiplicando y per z (o y volte z) si può scrivere in 4 modi: y × z, y * z, y-z, o solo yz. Il simbolo di moltiplicazione "×" di solito non viene usato, perché assomiglia troppo alla lettera x, che viene spesso usata come variabile. Inoltre, quando si moltiplica un'espressione più grande, si possono usare le parentesi: y (z+1).

Quando moltiplichiamo un numero e una lettera in algebra, scriviamo il numero davanti alla lettera: 5 × y = 5y. Quando il numero è 1, allora l'1 non viene scritto perché 1 volte qualsiasi numero è quel numero (1 × y = y) e quindi non è necessario.

Come nota a margine, non è necessario utilizzare le lettere x o y in algebra. Le variabili sono solo simboli che significano un numero o un valore sconosciuto, quindi è possibile utilizzare qualsiasi variabile. x e y sono però le più comuni.

Funzioni e grafici

Una parte importante dell'algebra è lo studio delle funzioni, poiché le funzioni appaiono spesso in equazioni che stiamo cercando di risolvere. Una funzione è come una macchina in cui si può mettere un numero (o dei numeri) e far uscire un certo numero (o dei numeri). Quando si usano le funzioni, i grafici possono essere strumenti potenti per aiutarci a studiare le soluzioni delle equazioni.

Un grafico è un'immagine che mostra tutti i valori delle variabili che rendono vera l'equazione o disuguaglianza. Di solito è facile da realizzare quando ci sono solo una o due variabili. Il grafico è spesso una linea, e se la linea non si piega o non va dritta su e giù può essere descritta dalla formula di base y = mx + b. La variabile b è l'intercetto y del grafico (dove la linea attraversa l'asse verticale) e m è la pendenza o la ripidezza della linea. Questa formula si applica alle coordinate di un grafico, dove ogni punto della retta è scritto (x, y).

In alcuni problemi matematici come l'equazione per una linea, ci possono essere più variabili (x e y in questo caso). Per trovare punti sulla retta, una variabile viene cambiata. La variabile che viene cambiata è chiamata variabile "indipendente". Poi si fa la matematica per fare un numero. Il numero che viene fatto è chiamato variabile "dipendente". La maggior parte delle volte la variabile indipendente è scritta come x e la variabile dipendente è scritta come y, per esempio, in y = 3x + 1. Questo viene spesso messo su un grafico, utilizzando un asse x (andando a sinistra e a destra) e un asse y (andando su e giù). Può anche essere scritta in forma di funzione: f(x) = 3x + 1. Quindi, in questo esempio, potremmo mettere 5 per x e ottenere y = 16. Mettere 2 per x otterrebbe y=7. E 0 per x otterrebbe y=1. Quindi ci sarebbe una linea che passa attraverso i punti (5,16), (2,7), e (0,1) come si vede nel grafico a destra.

Se x ha una potenza di 1, è una linea retta. Se è quadrata o qualche altra potenza, sarà curva. Se utilizza una disuguaglianza (< o > ), allora di solito parte del grafico è ombreggiato, sia sopra che sotto la linea.

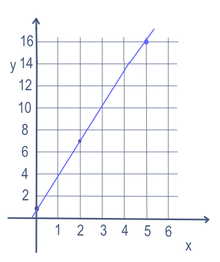
Equazione lineare per y=3x+1

Regole di algebra

In algebra, ci sono alcune regole che possono essere utilizzate per comprendere meglio le equazioni. Queste sono chiamate le regole dell'algebra. Anche se queste regole possono sembrare insensate o ovvie, è saggio capire che queste proprietà non valgono per tutti i rami della matematica. Pertanto, sarà utile sapere come queste regole assiomatiche sono dichiarate, prima di darle per scontate. Prima di passare alle regole, riflettere su due definizioni che verranno date.

Di fronte - l'opposto di uno stile di visualizzazione a} è - uno stile di visualizzazione -a} .
Reciproco - il reciproco di uno stile di visualizzazione è 1 uno stile di visualizzazione. ${\frac {1}{a}}$ .

Regole

Proprietà commutativa dell'addizione

Per "commutativa" si intende che una funzione ha lo stesso risultato se i numeri vengono scambiati. In altre parole, l'ordine dei termini in un'equazione non ha importanza. Quando l'operatore di due termini è un'aggiunta, si applica la "proprietà commutativa dell'aggiunta". In termini algebrici, questo dà a + b = b + a {\displaystyle a+b=b+a} a+b=b+a .

Si noti che questo non vale per la sottrazione! (ad es. a - b ≠ b - a {\a6} $a-b\neq b-a$ )

Proprietà commutativa della moltiplicazione

Quando l'operatore di due termini è una moltiplicazione, si applica la "proprietà commutativa della moltiplicazione". In termini algebrici, questo dà a ⋅ b = b ⋅ a {\an8} stile di visualizzazione a \cdot b=b \cdot a} $a\cdot b=b\cdot a$ .

Si noti che questo non vale per la divisione! (cioe' a b ≠ b a adisplaystyle (stile di visualizzazione) frac a ${\frac {a}{b}}\neq {\frac {b}{a}}$ , quando un ≠ b {\an8}}(*displaystyle a\neq b} $a\neq b$ )

Proprietà associativa di aggiunta

Per "associativo" si intende il raggruppamento di numeri. La proprietà associativa dell'addizione implica che, quando si aggiungono tre o più termini, non importa come questi termini sono raggruppati. Algebricamente, questo dà un + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} . Si noti che questo non tiene per sottrazione, ad esempio 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1} $1=0-(0-1)\neq (0-0)-1=-1$ (vedere la proprietà distributiva).

Proprietà associativa di moltiplicazione

La proprietà associativa della moltiplicazione implica che, quando si moltiplicano tre o più termini, non importa come questi termini sono raggruppati. Algebricamente, questo dà un ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\an8}(a \an8}(a \cdot b)\cdot c} $a\cdot (b\cdot c)=(a\cdot b)\cdot c$ . Si noti che questo non vale per la divisione, ad es. 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\a6} $2=1/(1/2)\neq (1/1)/2=1/2$ .

Proprietà distributiva

La proprietà distributiva stabilisce che la moltiplicazione di un numero per un altro termine può essere distribuita. Per esempio: a ⋅ ( b + c ) = a b + a c {\proprio stile di visualizzazione a \cdot (b+c)=ab+ac} $a\cdot (b+c)=ab+ac$ . (Non confondere questo con le proprietà associative! Per esempio, a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\a6} $a\cdot (b+c)\neq (a\cdot b)+c$ .

Proprietà di identità additiva

Per "identità" si intende la proprietà di un numero che è uguale a se stesso. In altre parole, esiste un'operazione di due numeri in modo che sia uguale alla variabile della somma. La proprietà "Identità additiva" indica che la somma di un numero qualsiasi e 0 è quel numero: a + 0 = a {\displaystyle a+0=a} a+0=a . Questo vale anche per la sottrazione: a - 0 = a {\displaystyle a-0=a} a-0=a .

Proprietà d'identità moltiplicativa

La proprietà di identità moltiplicativa afferma che il prodotto di un numero qualsiasi e 1 è quel numero: a ⋅ 1 = a {\i} $a\cdot 1=a$ . Questo vale anche per la divisione: a 1 = uno stile di visualizzazione {\a}{1}}=a} ${\frac {a}{1}}=a$ .

Proprietà additiva inversa

La proprietà additiva inversa è in qualche modo simile all'opposto della proprietà di identità dell'additivo. Quando un'operazione è la somma di un numero e del suo opposto, ed è uguale a 0, quell'operazione è una valida operazione algebrica. Algebricamente, essa afferma quanto segue: a - a = 0 {\displaystyle a-a=0} a-a=0 . L'inverso additivo di 1 è (-1).

Proprietà moltiplicativa inversa

La proprietà moltiplicativa inversa comporta che quando un'operazione è il prodotto di un numero e la sua reciproca, ed è uguale a 1, tale operazione è una valida operazione algebrica. Algebricamente, essa afferma quanto segue: a a = 1 {\displaystyle {\frac {a}{a}}}=1} ${\frac {a}{a}}=1$ . L'inverso moltiplicativo di 2 è 1/2.

Algebra avanzata

Oltre all'"algebra elementare", o algebra di base, esistono forme avanzate di algebra, insegnate nei college e nelle università, come l'algebra astratta, l'algebra lineare e l'algebra universale. Questo include come usare una matrice per risolvere molte equazioni lineari contemporaneamente. L'algebra astratta è lo studio delle cose che si trovano nelle equazioni, andando oltre i numeri fino al più astratto con gruppi di numeri.

Molti problemi di matematica riguardano la fisica e l'ingegneria. In molti di questi problemi di fisica il tempo è una variabile. Il tempo usa la lettera t. L'uso delle idee di base in algebra può aiutare a ridurre un problema matematico alla sua forma più semplice, rendendo più facile la soluzione di problemi difficili. L'energia è e, la forza è f, la massa è m, l'accelerazione è a e la velocità della luce è a volte c. Questo è usato in alcune famose equazioni, come f = ma ed e=mc^2 (anche se è stata necessaria una matematica più complessa oltre l'algebra per arrivare a quest'ultima equazione).

Pagine correlate

Elenco degli argomenti di matematica
Ordine delle operazioni
Parabola
Sistema di algebra computerizzata

Domande e risposte

D: Che cos'è l'algebra?

R: L'algebra è una parte della matematica che utilizza le variabili per rappresentare un valore che non è ancora noto.

D: Che cosa significa il segno di uguale nell'algebra?

R: Il segno di uguale (=) indica un'equazione in algebra.

D: Che cos'è una funzione in algebra?

R: Una funzione in algebra è un tipo speciale di equazione che trasforma sempre un ingresso in un'uscita.

D: Come si può usare l'algebra per risolvere i problemi reali?

R: L'algebra può essere utilizzata per risolvere problemi reali, perché le regole dell'algebra funzionano nella vita reale e i numeri possono essere utilizzati per rappresentare i valori di cose reali. La fisica, l'ingegneria e la programmazione informatica sono settori che utilizzano costantemente l'algebra. È utile conoscerla anche nella misurazione, nell'edilizia e negli affari, in particolare nella contabilità.

D: Quali sono alcune operazioni matematiche utilizzate sui numeri in algebra?

R: Nell'algebra si utilizzano le regole dei numeri e le operazioni matematiche come aggiungere, sottrarre, moltiplicare e dividere sui numeri. Le operazioni più avanzate coinvolgono gli esponenti, a partire dai quadrati e dalle radici quadrate.

D: Quali sono gli esempi di equazioni utilizzate in algebra?

R: Gli esempi di equazioni utilizzate in algebra includono le equazioni lineari (l'equazione di una linea retta) e le equazioni quadratiche che hanno variabili al quadrato (moltiplicate per se stesse).